
在本章中约定用A,B,C分别表示△ABC的三个内角,a, b, c分别表示它们所对的各边长,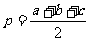 为半周长。
为半周长。
1.正弦定理: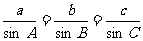 =2R(R为△ABC外接圆半径)。
=2R(R为△ABC外接圆半径)。
推论1:△ABC的面积为S△ABC=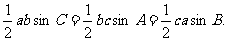
推论2:在△ABC中,有bcosC+ccosB=a.
推论3:在△ABC中,A+B=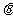 ,解a满足
,解a满足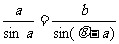 ,则a=A.
,则a=A.
正弦定理可以在外接圆中由定义证明得到,这里不再给出,下证推论。先证推论1,由正弦函数定义,BC边上的高为bsinC,所以S△ABC=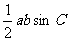 ;再证推论2,因为B+C=
;再证推论2,因为B+C= -A,所以sin(B+C)=sinA,即sinBcosC+cosBsinC=sinA,两边同乘以2R得bcosC+ccosB=a;再证推论3,由正弦定理
-A,所以sin(B+C)=sinA,即sinBcosC+cosBsinC=sinA,两边同乘以2R得bcosC+ccosB=a;再证推论3,由正弦定理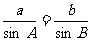 ,所以
,所以 ,即sinasin(
,即sinasin(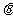 -A)=sin(
-A)=sin(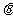 -a)sinA,等价于
-a)sinA,等价于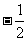 [cos(
[cos(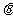 -A+a)-cos(
-A+a)-cos(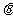 -A-a)]=
-A-a)]=  [cos(
[cos(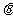 -a+A)-cos(
-a+A)-cos(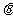 -a-A)],等价于cos(
-a-A)],等价于cos(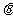 -A+a)=cos(
-A+a)=cos(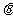 -a+A),因为0<
-a+A),因为0<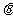 -A+a,
-A+a,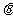 -a+A<
-a+A< . 所以只有
. 所以只有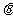 -A+a=
-A+a=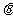 -a+A,所以a=A,得证。
-a+A,所以a=A,得证。
9.已知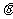 i
i ,tan
,tan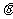 1tan
1tan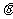 2…tan
2…tan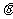 n=2
n=2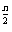 , n∈N+, 若对任意一组满足上述条件的
, n∈N+, 若对任意一组满足上述条件的
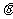 1,
1,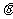 2,…,
2,…,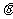 n都有cos
n都有cos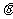 1+cos
1+cos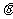 2+…+cos
2+…+cos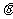 n≤λ,求λ的最小值。
n≤λ,求λ的最小值。
8.求的有的实数a, 使cosa, cos2a, cos4a, …, cos2na, …中的每一项均为负数。
7.在△ABC中,求sinA+sinB+sinC-cosA-cosB-cosC的最大值。
6. 设n, m都是正整数,并且n>m,求证:对一切x 都有2|sinnx-cosnx|≤3|sinnx-cosnx|.
都有2|sinnx-cosnx|≤3|sinnx-cosnx|.
5. 求实数a的取值范围,使得对任意实数x和任意
求实数a的取值范围,使得对任意实数x和任意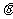
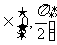 ,恒有(x+3+2sin
,恒有(x+3+2sin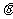 cos
cos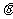 )2+(x+asin
)2+(x+asin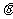 +asin
+asin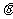 )2≥
)2≥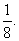
4.已知α,β,γ为锐角,且cos2α+cos2β+cos2γ=1,求证; π<α+β+γ<π.
π<α+β+γ<π.
3. 设x1, x2,…, xn,…, y1, y2,…, yn,…满足x1=y1=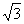 , xn+1=xn+
, xn+1=xn+ , yn+1=
, yn+1=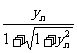 ,求证:2<xnyn<3(n≥2).
,求证:2<xnyn<3(n≥2).
2. 已知a为锐角,n≥2, n∈N+,求证: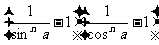 ≥2n-2
≥2n-2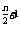 +1.
+1.
1.已知x>0, y>0, 且x+y<π,求证:w(w-1)sin(x+y)+w(sinx-siny)+siny>0①(w∈R).
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com