
定义1 既有大小又有方向的量,称为向量。画图时用有向线段来表示,线段的长度表示向量的模。向量的符号用两个大写字母上面加箭头,或一个小写字母上面加箭头表示。书中用黑体表示向量,如a. |a|表示向量的模,模为零的向量称为零向量,规定零向量的方向是任意的。零向量和零不同,模为1的向量称为单位向量。
定义2 方向相同或相反的向量称为平行向量(或共线向量),规定零向量与任意一个非零向量平行和结合律。
定理1 向量的运算,加法满足平行四边形法规,减法满足三角形法则。加法和减法都满足交换律和结合律。
定理2 非零向量a, b共线的充要条件是存在实数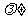 0,使得a=
0,使得a= f
f
定理3 平面向量的基本定理,若平面内的向量a, b不共线,则对同一平面内任意向是c,存在唯一一对实数x, y,使得c=xa+yb,其中a, b称为一组基底。
定义3 向量的坐标,在直角坐标系中,取与x轴,y轴方向相同的两个单位向量i, j作为基底,任取一个向量c,由定理3可知存在唯一一组实数x, y,使得c=xi+yi,则(x, y)叫做c坐标。
定义4 向量的数量积,若非零向量a, b的夹角为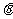 ,则a, b的数量积记作a·b=|a|·|b|cos
,则a, b的数量积记作a·b=|a|·|b|cos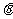 =|a|·|b|cos<a, b>,也称内积,其中|b|cos
=|a|·|b|cos<a, b>,也称内积,其中|b|cos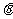 叫做b在a上的投影(注:投影可能为负值)。
叫做b在a上的投影(注:投影可能为负值)。
定理4 平面向量的坐标运算:若a=(x1, y1), b=(x2, y2),
1.a+b=(x1+x2, y1+y2), a-b=(x1-x2, y1-y2),
2 λa=(λx1,
λy1), a·(b+c)=a·b+a·c,
λa=(λx1,
λy1), a·(b+c)=a·b+a·c,
9.设P是△ABC内一点,点P至BC,CA,AB的垂线分别为PD,PE,PF(D,E,F是垂足),求证:PA·PB·PC≥(PD+PE)·(PE+PF)·(PF+PD),并讨论等号成立之条件。
8.设四边形ABCD内接于圆,BA和CD延长后交于点R,AD和BC延长后交于点P, A,
A, B,
B, C指的都是△ABC的内角,求证:若AC与BD交于点Q,则
C指的都是△ABC的内角,求证:若AC与BD交于点Q,则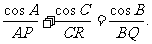
7.已知一凸四边形的边长依次为a, b, c, d,外接圆半径为R,如果a2+b2+c2+d2=8R2,试问对此四边形有何要求?
6.AP,AQ,AR,AS是同一个圆中的四条弦,已知 PAQ=
PAQ= QAR=
QAR= RAS,求证:AR(AP+AR)=AQ(AQ+AS)。
RAS,求证:AR(AP+AR)=AQ(AQ+AS)。
5.已知等腰梯形ABCD,G是对角线BD与AC的交点,过点G作EF与上、下底平行,点E和F分别在AB和CD上,求证: AFB=900的充要条件是AD+BC=CD。
AFB=900的充要条件是AD+BC=CD。
4.已知凸五边形ABCDE,其中 ABC=
ABC= AED=900,
AED=900, BAC=
BAC= EAD,BD与CE交于点O,求证:AO
EAD,BD与CE交于点O,求证:AO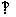 BE。
BE。
3.已知△ABC,其中BC上有一点M,且△ABM与△ACM的内切圆大小相等,求证: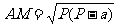 ,此处
,此处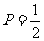 (a+b+c), a, b, c分别为△ABC对应三边之长。
(a+b+c), a, b, c分别为△ABC对应三边之长。
2.设四边形ABCD的对角线交于点O,点M和N分别是AD和BC的中点,点H1,H2(不重合)分别是△AOB与△COD的垂心,求证:H1H2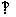 MN。
MN。
1.已知等腰△ABC,AB=AC,一半圆以BC的中点为圆心,且与两腰AB和AC分别相切于点D和G,EF与半圆相切,交AB于点E,交AC于点F,过E作AB的垂线,过F作AC的垂线,两垂线相交于P,作PQ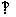 BC,Q为垂足。求证:
BC,Q为垂足。求证: ,此处
,此处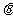 =
= B。
B。
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com