
4.设s, t为非零实数,a, b为单位向量,若|sa+tb|=|ta-sb|,则a和b的夹角为__________.
3.已知a=y-x, b=2x-y, |a|=|b|=1, a·b=0,则|x|+|y|=__________.
2.已知正六边形ABCDEF,在下列表达式中:①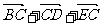 ;②
;② ;③
;③ 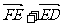 ;④
;④ 与
与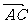 ,相等的有__________.
,相等的有__________.
1.以下命题中正确的是__________.
①a=b的充要条件是|a|=|b|,且a//b;②(a·b)·c=(a·c)·b;③若a·b=a·c,则b=c;④若a, b不共线,则xa+yb=ma+nb的充要条件是x=m, y=n;⑤若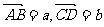 ,且a, b共线,则A,B,C,D共线;⑥a=(8, 1)在b=(-3, 4)上的投影为-4。
,且a, b共线,则A,B,C,D共线;⑥a=(8, 1)在b=(-3, 4)上的投影为-4。
4.向量的坐标运算。
例7 已知四边形ABCD是正方形,BE//AC,AC=CE,EC的延长线交BA的延长线于点F,求证:AF=AE。
3.利用数量积证明垂直。
例5 给定非零向量a, b. 求证:|a+b|=|a-b|的充要条件是a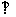 b.
b.
例6 已知△ABC内接于⊙O,AB=AC,D为AB中点,E为△ACD重心。求证:OE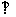 CD。
CD。
2.证利用定理2证明共线。
例4 △ABC外心为O,垂心为H,重心为G。求证:O,G,H为共线
,且OG:GH=1:2。
1.向量定义和运算法则的运用。
例1 设O是正n边形A1A2…An的中心,求证:
例2 给定△ABC,求证:G是△ABC重心的充要条件是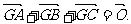
例3 在凸四边形ABCD中,P和Q分别为对角线BD和AC的中点,求证:AB2+BC2+CD2+DA2=AC2+BD2+4PQ2。
4. a//b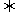 x1y2=x2y1,
a
x1y2=x2y1,
a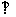 b
b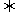 x1x2+y1y2=0.
x1x2+y1y2=0.
定义5 若点P是直线P1P2上异于p1,p2的一点,则存在唯一实数λ,使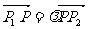 ,λ叫P分
,λ叫P分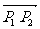 所成的比,若O为平面内任意一点,则
所成的比,若O为平面内任意一点,则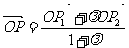 。由此可得若P1,P,P2的坐标分别为(x1, y1), (x, y), (x2, y2),则
。由此可得若P1,P,P2的坐标分别为(x1, y1), (x, y), (x2, y2),则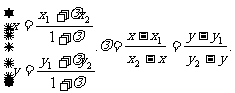
定义6 设F是坐标平面内的一个图形,将F上所有的点按照向量a=(h, k)的方向,平移|a|=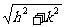 个单位得到图形
个单位得到图形 ,这一过程叫做平移。设p(x, y)是F上任意一点,平移到
,这一过程叫做平移。设p(x, y)是F上任意一点,平移到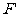 上对应的点为
上对应的点为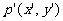 ,则
,则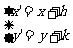 称为平移公式。
称为平移公式。
定理5 对于任意向量a=(x1, y1), b=(x2, y2), |a·b|≤|a|·|b|,并且|a+b|≤|a|+|b|.
[证明] 因|a|2·|b|2-|a·b|2=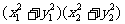 -(x1x2+y1y2)2=(x1y2-x2y1)2≥0,又|a·b|≥0, |a|·|b|≥0,
-(x1x2+y1y2)2=(x1y2-x2y1)2≥0,又|a·b|≥0, |a|·|b|≥0,
所以|a|·|b|≥|a·b|.
由向量的三角形法则及直线段最短定理可得|a+b|≤|a|+|b|.
注:本定理的两个结论均可推广。1)对n维向量,a=(x1, x2,…,xn),b=(y1, y2, …, yn),同样有|a·b|≤|a|·|b|,化简即为柯西不等式: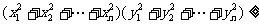 (x1y1+x2y2+…+xnyn)2≥0,又|a·b|≥0, |a|·|b|≥0,
(x1y1+x2y2+…+xnyn)2≥0,又|a·b|≥0, |a|·|b|≥0,
所以|a|·|b|≥|a·b|.
由向量的三角形法则及直线段最短定理可得|a+b|≤|a|+|b|.
注:本定理的两个结论均可推广。1)对n维向量,a=(x1, x2,…,xn), b=(y1, y2, …, yn),同样有|a·b|≤|a|·|b|,化简即为柯西不等式: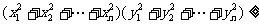 (x1y1+x2y2+…+xnyn)2。
(x1y1+x2y2+…+xnyn)2。
2)对于任意n个向量,a1, a2, …,an,有| a1, a2, …,an|≤| a1|+|a2|+…+|an|。
3.a·b=x1x2+y1y2,
cos(a, b)=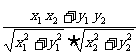 (a,
b
(a,
b 0),
0),
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com