
7.若a, b∈R+,则a+b=1,以下结论成立是__________.① a4+b4≥ ;②
;② ≤a3+b3<1;③
≤a3+b3<1;③ ;④
;④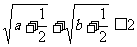 ;⑤
;⑤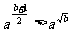 ;⑥
;⑥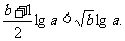
6.“a+b=4”是“不等式|x-a|+|x-b|<8的解集是{x|-2<x<6}”的____________条件.
5.若不等式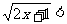 x+a的解是x>m,则m的最小值是____________.
x+a的解是x>m,则m的最小值是____________.
4.若不等式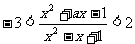 对所有实数x成立,则a的取值范围是____________.
对所有实数x成立,则a的取值范围是____________.
3.已知a, b, c∈R,且a2+b2+c2=1, ab+bc+ca的最大值为M,最小值为N,则MN=___________.
2.已知x∈R+,则 的最小值是____________.
的最小值是____________.
1.已知0<x<1,a, b∈R+,则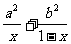 的最小值是____________.
的最小值是____________.
2.几个常用的不等式。
(1)柯西不等式:若ai∈R, bi∈R, i=1, 2, …, n,则
等号当且仅当存在λ∈R,使得对任意i=1, 2, , n, ai=λbi,
变式1:若ai∈R, bi∈R, i=1, 2, …, n,则
等号成立条件为ai=λbi,(i=1, 2, …, n)。
变式2:设ai, bi同号且不为0(i=1, 2, …, n),则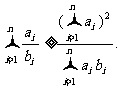
等号成立当且仅当b1=b2=…=bn.
(2)平均值不等式:设a1, a2,…,an∈R+,记Hn=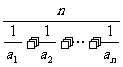 , Gn=
, Gn=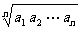 , An=
, An=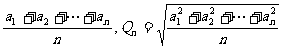 ,则Hn≤Gn≤An≤Qn. 即调和平均≤几何平均≤算术平均≤平方平均。
,则Hn≤Gn≤An≤Qn. 即调和平均≤几何平均≤算术平均≤平方平均。
其中等号成立的条件均为a1=a2=…=an.
[证明] 由柯西不等式得An≤Qn,再由Gn≤An可得Hn≤Gn,以下仅证Gn≤An.
1)当n=2时,显然成立;
2)设n=k时有Gk≤Ak,当n=k+1时,记 =Gk+1.
=Gk+1.
因为a1+a2+…+ak+ak+1+(k-1)Gk+1≥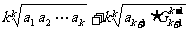
≥ 2kGk+1,
2kGk+1,
所以a1+a2+…+ak+1≥(k+1)Gk+1,即Ak+1≥Gk+1.
所以由数学归纳法,结论成立。
(3)排序不等式:若两组实数a1≤a2≤…≤an且b1≤b2≤…≤bn,则对于b1, b2, …, bn的任意排列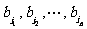 ,有a1bn+a2bn-1+…+anb1≤
,有a1bn+a2bn-1+…+anb1≤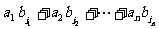 ≤a1b1+a2b2+…+anbn.
≤a1b1+a2b2+…+anbn.
[证明] 引理:记A0=0,Ak= ,则
,则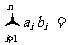
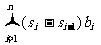 =
=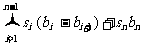 (阿贝尔求和法)。
(阿贝尔求和法)。
证法一:因为b1≤b2≤…≤bn,所以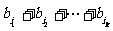 ≥b1+b2+…+bk.
≥b1+b2+…+bk.
记sk=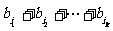 -( b1+b2+…+bk),则sk≥0(k=1, 2, …, n)。
-( b1+b2+…+bk),则sk≥0(k=1, 2, …, n)。
所以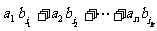 -(a1b1+a2b2+…+anbn)=
-(a1b1+a2b2+…+anbn)=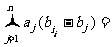
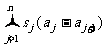 +snan≤0.
+snan≤0.
最后一个不等式的理由是aj-aj+1≤0(j=1, 2, …, n-1, sn=0),
所以右侧不等式成立,同理可证左侧不等式。
证法二:(调整法)考察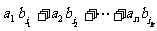 ,若
,若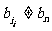 ,则存在。
,则存在。
若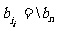 (j≤n-1),则将
(j≤n-1),则将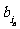 与
与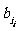 互换。
互换。
因为
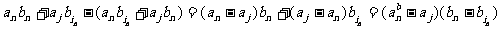 ≥0,
≥0,
所 调整后,和是不减的,接下来若 ,则继续同样的调整。至多经n-1次调整就可将乱序和调整为顺序和,而且每次调整后和是不减的,这说明右边不等式成立,同理可得左边不等式。
,则继续同样的调整。至多经n-1次调整就可将乱序和调整为顺序和,而且每次调整后和是不减的,这说明右边不等式成立,同理可得左边不等式。
例15 已知a1, a2,…,an∈R+,求证;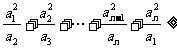 a1+a2+…+an.
a1+a2+…+an.
注:本讲的每种方法、定理都有极广泛的应用,希望读者在解题中再加以总结。
1.不等式证明的基本方法。
(1)比较法,在证明A>B或A<B时利用A-B与0比较大小,或把 (A,B>0)与1比较大小,最后得出结论。
(A,B>0)与1比较大小,最后得出结论。
例1 设a, b, c∈R+,试证:对任意实数x, y, z, 有x2+y2+z2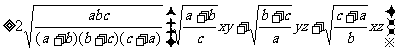
例2 若a<x<1,比较大小:|loga(1-x)|与|loga(1+x)|.
(2)分析法,即从欲证不等式出发,层层推出使之成立的充分条件,直到已知为止,叙述方式为:要证……,只需证……。
例3 已知a, b, c∈R+,求证:a+b+c-3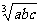 ≥a+b
≥a+b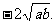
(3)数学归纳法。
例5 对任意正整数n(≥3),求证:nn+1>(n+1)n.
(4)反证法。
例6 设实数a0, a1,…,an满足a0=an=0,且a0-2a1+a2≥0, a1-2a2+a3≥0,…, an-2-2an-1+an≥0,求证ak≤0(k=1, 2,…, n-1).
(5)分类讨论法。
例7 已知x, y, z∈R+,求证: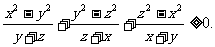
(6)放缩法,即要证A>B,可证A>C1, C1≥C2,…,Cn-1≥Cn, Cn>B(n∈N+).
例8 求证:
例9 已知a, b, c是△ABC的三条边长,m>0,求证: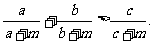
(7)引入参变量法。
例10 已知x, y∈R+, l, a,
b为待定正数,求f(x,
y)= 的最小值。
的最小值。
例11 设x1≥x2≥x3≥x4≥2, x2+x3+x4≥x1,求证:(x1+x2+x3+x4)2≤4x1x2x3x4.
(8)局部不等式。
例12 已知x, y, z∈R+,且x2+y2+z2=1,求证: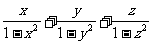
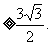
例13 已知0≤a, b, c≤1,求证: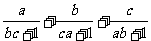 ≤2。
≤2。
(9)利用函数的思想。
例14 已知非负实数a, b, c满足ab+bc+ca=1,求f(a, b, c)=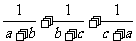 的最小值。
的最小值。
不等式的基本性质:
(1)a>b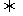 a-b>0;
(2)a>b, b>c
a-b>0;
(2)a>b, b>c a>c;
a>c;
(3)a>b a+c>b+c; (4)a>b, c>0
a+c>b+c; (4)a>b, c>0 ac>bc;
ac>bc;
(5)a>b, c<0 ac<bc; (6)a>b>0,
c>d>0
ac<bc; (6)a>b>0,
c>d>0 ac>bd;
ac>bd;
(7)a>b>0, n∈N+ an>bn; (8)a>b>0,
n∈N+
an>bn; (8)a>b>0,
n∈N+
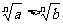 ;
;
(9)a>0, |x|<a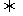 -a<x<a, |x|>a
-a<x<a, |x|>a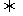 x>a或x<-a;
x>a或x<-a;
(10)a, b∈R,则|a|-|b|≤|a+b|≤|a|+|b|;
(11)a, b∈R,则(a-b)2≥0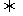 a2+b2≥2ab;
a2+b2≥2ab;
(12)x, y, z∈R+,则x+y≥2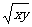 , x+y+z
, x+y+z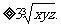
前五条是显然的,以下从第六条开始给出证明。
(6)因为a>b>0, c>d>0,所以ac>bc, bc>bd,所以ac>bd;重复利用性质(6),可得性质(7);再证性质(8),用反证法,若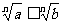 ,由性质(7)得
,由性质(7)得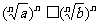 ,即a≤b,与a>b矛盾,所以假设不成立,所以
,即a≤b,与a>b矛盾,所以假设不成立,所以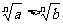 ;由绝对值的意义知(9)成立;-|a|≤a≤|a|,
-|b|≤b≤|b|,所以-(|a|+|b|)≤a+b≤|a|+|b|,所以|a+b|≤|a|+|b|;下面再证(10)的左边,因为|a|=|a+b-b|≤|a+b|+|b|,所以|a|-|b|≤|a+b|,所以(10)成立;(11)显然成立;下证(12),因为x+y-2
;由绝对值的意义知(9)成立;-|a|≤a≤|a|,
-|b|≤b≤|b|,所以-(|a|+|b|)≤a+b≤|a|+|b|,所以|a+b|≤|a|+|b|;下面再证(10)的左边,因为|a|=|a+b-b|≤|a+b|+|b|,所以|a|-|b|≤|a+b|,所以(10)成立;(11)显然成立;下证(12),因为x+y-2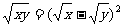 ≥0,所以x+y≥
≥0,所以x+y≥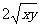 ,当且仅当x=y时,等号成立,再证另一不等式,令
,当且仅当x=y时,等号成立,再证另一不等式,令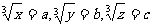 ,因为x3+b3+c3-3abc =(a+b)3+c3-3a2b-3ab2-3abc
=(a+b)3+c3-3ab(a+b+c)=(a+b+c)[(a+b)2-(a+b)c+c2]-3ab(a+b+c)=(a+b+c)(a2+b2+c2-ab-bc-ca)=
,因为x3+b3+c3-3abc =(a+b)3+c3-3a2b-3ab2-3abc
=(a+b)3+c3-3ab(a+b+c)=(a+b+c)[(a+b)2-(a+b)c+c2]-3ab(a+b+c)=(a+b+c)(a2+b2+c2-ab-bc-ca)=
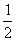 (a+b+c)[(a-b)2+(b-c)2+(c-a)2]
≥0,所以a3+b3+c3≥3abc,即x+y+z≥
(a+b+c)[(a-b)2+(b-c)2+(c-a)2]
≥0,所以a3+b3+c3≥3abc,即x+y+z≥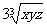 ,等号当且仅当x=y=z时成立。
,等号当且仅当x=y=z时成立。
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com