
1.一天中,观看到卫星被阳光照射面积最大的时间(北京时间)是
A.1时前后 B.7时前后 C.11时前后 D.13时前后
86、交流的成本
前段时间,太太突然发现家中交流成本付出十分“惨重”。两人手机话费加起来要300多元,电话费要50多元,还要宽带费68元。太太发现花了400多元的“交流费”,我们似乎什么也没有得到。
举一个例子。2月29日那天,太太列举她一天所接的电话,两个是她妈打来的,问她是不是在上班。一个是她姐打来的,问她这么多天没看到了,是不是准备一起回家。还有一个是打错的电话,太太说她的电话费11元,却什么都没有得到。
经太太这样一计算,我突然觉得这个世界实在十分荒唐。每个人都花了很大的代价在进行沟通,但许多信息的确是多余的,我们根本没有从中得到了什么,反而失去了许多宝贵的时间。现在有一种包月的手机话费促销方案,500元可以打到1200元,可以想象,一个人在对自己的手机话费进行包月时,他就要千方百计让自己的手机话费达到了1200元,1200元的话费可以说多少话,其间需要多少时间?又需要多少精力?又占据他人多少时间和精力?如果计算起来,那绝对是一种很没意思的事。
而现代人最大的谬误就是认为交流越多越好,而对自己失去的东西却常常忽略不计。
85、“蓝牙”是什么牙
超凡的快乐让我们热爱世界,巨大的悲痛让我们理解世界。
--德国社会学家内尔伯恩对快乐与悲痛的理解
房子和财富是从父亲那里继承下来的,而一个可人的妻子则是从上帝那里得到的礼物。
--美国格言,提醒所有男人应该珍惜自己最珍贵的礼物
生活的悲剧性不在于一个人输了,而在于他差一点赢了。
--海伍德?布朗
第一句更多是说给马上要走向工作岗位的同学的,一句大实话:社会和学校很不一样。第二句话,是对每个同学说的,要安分守己。“安分守己”不是一个贬义词,甚至不是一个中性词,“安分”是不容易的,在这个时代“守己”则更不容易。
--北京大学法学院2003届本科毕业生典礼上的致辞
“新结构主义”究竟是一种文化思潮还是一处房产?
“蓝牙”是什么牙?
“纳米”是什么米?
“新亚洲之美”是什么美?……
--一位中学老师谈新名词的新困惑:几乎所有商品都被披上了概念的外衣,还有什么东西可以一目了然?
84、理由
凡事都有理由,食因为饥,睡因为困,坐车因为怕走路。有些事情成了习惯,似乎不需要理由,其实理由潜在着,只是我们不怎么发觉罢了。
我们走进大小机关,碰上的第一句话永远是“找谁?”随后还要填写一张找谁的单子。似乎有熟人找熟人才是人们去这种地方的正当理由,多少年来习以为常,天经地义。于是,来也熟人去也熟人成了公共机关最不该有又是最特有的风景。
我们平时乘车,车子坏在半路,司机售票员哪一次宣布理由不是气壮如牛?没油了!没水了!出故障了!下车吧!我从来不敢奢望听见一句道歉声,但也以为,即使你们不认错,也不必让乘客都是一副灰溜溜的模样,好像车不走了是因为乘客出门不择吉日。
我们平时办事,什么上级有规定、领导有指示、内部有文件、这不归我管、头不在、我不知道、你找别的部门吧,种种拒绝的理由乍听上去都像那么一回事,但进一步,或者说寻找其终极理由,没有一个可以称得上是理由!比如你所谓的规定、指示、文件在哪里?经过了哪些合法程序?谁给你的权力?你有没有这样的权限?比如归谁管、头在不在,是你们自己的事情!跟我有什么关系?我面对的是你这个部门!比如你不知道,那是你的失职,你应该引咎辞职,怎么还好意思说出来!
前几天,我还听见了这样的对话,可供一笑。
“你的申请不批准。”“为什么?”“有规定。”“规定在哪儿?”“不能给你看!”
“这里是办公室吗?”“是。”“你能介绍情况吗?”“不能。”“为什么?”“我刚进门。”“过一会儿可以吗?”“也不行。”“为什么?”“我刚调来。”
6.已知非负实数a, b, c满足a+b+c=1,求证:2≤(1-a2)2+(1-b2)2+(1-c2)2≤(1+a)(1+b)(1+c),并求出等号成立的条件。

5.已知x, y, z∈R+,求证:(xy+yz+zx)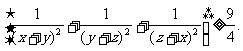
4.给定正数λ和正整数n(n≥2),求最小的正数M(λ),使得对于所有非负数x1, x2,…,xn ,有M(λ)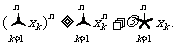
3.设f(x)=x2+a,记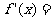 f(x), fn(x)=f(fn-1(x))(n=2, 3, …),M={a∈R|对所有正整数n, |fn(0)| ≤2},求证:
f(x), fn(x)=f(fn-1(x))(n=2, 3, …),M={a∈R|对所有正整数n, |fn(0)| ≤2},求证: 。
。
2.设整数x1, x2, …,xn与y1, y2, …, yn满足1<x1<x2<…<xn<y1<y2<…<ym, x1+x2+…+xn>y1+y2+…+ym,求证:x1x2xn>y1y2…ym.
1.设正实数x, y, z满足x+y+z=1,求证: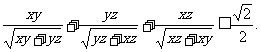
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com