
3.围绕经济社会发展重点,2009年,新疆自治区拟完成16件地方性法规和政府规章的立法。这表明我国民族自治地区依法享有 ( )
A.独立的司法权 B.高度的自治权 C.民族自治权 D.国家立法权
2.马克思主义在民族问题上的基本观点和实现民族团结的政治基础是 ( )
A.民族自治 B.各民族共同繁荣
C.民族平等 D.民族互助
1.在民族的四个特征中,作为民族形成的物质基础和区别民族的最显著特点的分别是( )
A.共同地域和共同经济生活 B.共同经济生活和共同心理素质
C.共同心理素质和共同语言 D.共同繁荣和共同地域
本类考题是高考数学题中综合性最强,难度最大的考题之一,通常以证明变量的相等关系或不等关系为主,证明时要注意到参变量与函数在条件区间中与其他变量的关系,结合等式或不等式的性质来证明等量或不等量关系。而利用导数法解函数与数例综合题时,则要注意寻找数列公差、公比、求和、递推等知识点与函数性质来综合求解。
例4(08湖南文21).已知函数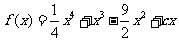 有三个极值点。
有三个极值点。
(I)证明: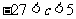 ;
;
(II)若存在实数c,使函数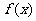 在区间
在区间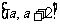 上单调递减,求
上单调递减,求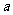 的取值范围。
的取值范围。
解:(I)因为函数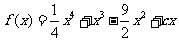 有三个极值点,
有三个极值点,
所以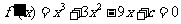 有三个互异的实根.
有三个互异的实根.
设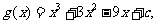 则
则
当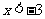 时,
时,
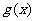 在
在 上为增函数;
上为增函数;
当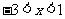 时,
时,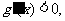
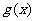 在
在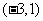 上为减函数;
上为减函数;
当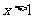 时,
时,
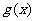 在
在 上为增函数;
上为增函数;
所以函数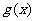 在
在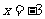 时取极大值,在
时取极大值,在 时取极小值.
时取极小值.
当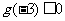 或
或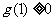 时,
时,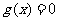 最多只有两个不同实根.
最多只有两个不同实根.
因为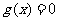 有三个不同实根, 所以
有三个不同实根, 所以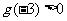 且
且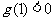 .
.
即 ,且
,且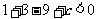 ,
,
解得 且
且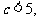 故
故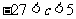 .
.
(II)由(I)的证明可知,当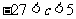 时,
时, 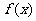 有三个极值点.
有三个极值点.
不妨设为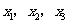 (
(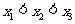 ),则
),则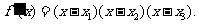
所以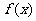 的单调递减区间是
的单调递减区间是 ,
,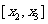
若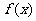 在区间
在区间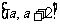 上单调递减,
上单调递减,
则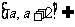
 , 或
, 或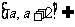
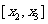 ,
,
若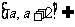
 ,则
,则 .由(I)知,
.由(I)知, ,于是
,于是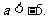
若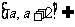
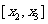 ,则
,则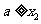 且
且 .由(I)知,
.由(I)知,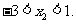
又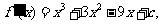 当
当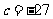 时,
时,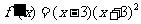 ;
;
当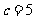 时,
时,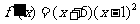 .
.
因此, 当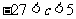 时,
时,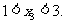 所以
所以 且
且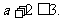
即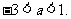 故
故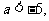 或
或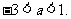 反之, 当
反之, 当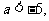 或
或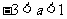 时,
时,
总可找到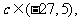 使函数
使函数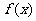 在区间
在区间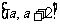 上单调递减.
上单调递减.
综上所述, 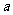 的取值范围是
的取值范围是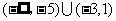
例5(08福建理)已知函数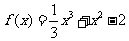 .
.
(Ⅰ)设{an}是正数组成的数列,前n项和为Sn,其中a1=3.若点 (n∈N*)在函数y=f′(x)的图象上,求证:点(n, Sn)也在y=f′(x)的图象上;
(n∈N*)在函数y=f′(x)的图象上,求证:点(n, Sn)也在y=f′(x)的图象上;
(Ⅱ)求函数f(x)在区间(a-1, a)内的极值.
解:(Ⅰ)证明:因为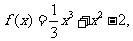 所以
所以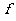 ′(x)=x2+2x,
′(x)=x2+2x,
由点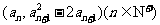 在函数y=f′(x)的图象上,
在函数y=f′(x)的图象上,
得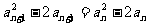 ,即
,即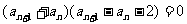 ,
,
又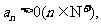 所以
所以 ,又因为
,又因为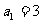 ,
,
所以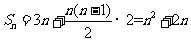 ,又因为
,又因为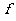 ′(n)=n2+2n,所以
′(n)=n2+2n,所以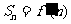 ,
,
故点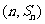 也在函数y=f′(x)的图象上.
也在函数y=f′(x)的图象上.
(Ⅱ)解: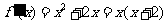 ,
,
由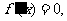 得
得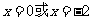 .
.
当x变化时,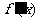 ﹑
﹑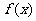 的变化情况如下表:
的变化情况如下表:
|
注意到 ,从而
,从而
①当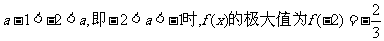 ,此时
,此时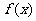 无极小值;
无极小值;
②当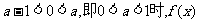 的极小值为
的极小值为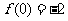 ,此时
,此时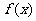 无极大值;
无极大值;
③当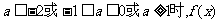 既无极大值又无极小值.
既无极大值又无极小值.
17.[考查分析]本题考查函数及求最值问题。
解:设楼房每平方米的平均综合费为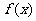 元,则
元,则

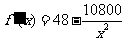
令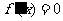 得
得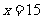
当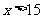 时,
时,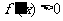 ;当
;当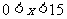 时,
时,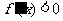
因此当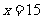 时,
时,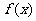 取最小值
取最小值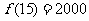
答:为了楼房每平方米的平均综合费最少,该楼房应建为15层
导函数的几何意义在于导函数在该点的值是原函数在该点和切线的斜率,于是利用导数法求解解析几何问题,就是要利用这一斜率与已知条件结合起来,使问题得到简化。而利用导函数求解应用题一般落实在函数建模和利用求导法判断所建模型函数的增减区间与极值点来简化求解过程。
例6()
设函数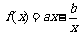 ,曲线
,曲线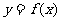 在点
在点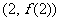 处的切线方程为
处的切线方程为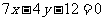 。
。
(1)求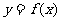 的解析式;
的解析式;
(2)证明:曲线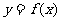 上任一点处的切线与直线
上任一点处的切线与直线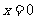 和直线
和直线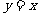 所围成的三角形面积为定值,并求此定值。
所围成的三角形面积为定值,并求此定值。
21.解:
(Ⅰ)方程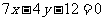 可化为
可化为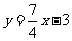 .
.
当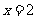 时,
时, .又
.又 ,
,
于是 解得
解得
故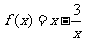 .
.
(Ⅱ)设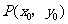 为曲线上任一点,由
为曲线上任一点,由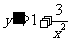 知曲线在点
知曲线在点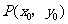 处的切线方程为
处的切线方程为
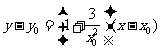 ,
,
即 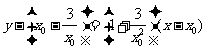 .
.
令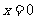 得
得 ,从而得切线与直线
,从而得切线与直线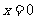 的交点坐标为
的交点坐标为 .
.
令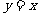 得
得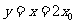 ,从而得切线与直线
,从而得切线与直线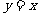 的交点坐标为
的交点坐标为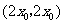 .······· 10分
.······· 10分
所以点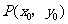 处的切线与直线
处的切线与直线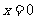 ,
,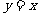 所围成的三角形面积为
所围成的三角形面积为
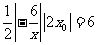 .
.
故曲线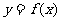 上任一点处的切线与直线
上任一点处的切线与直线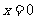 ,
,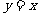 所围成的三角形的面积为定值,此定值为
所围成的三角形的面积为定值,此定值为 .
.
例7(08广东文17)某单位用2160万元购得一块空地,计划在该地块上建造一栋至少10层、每层2000平方米的楼房.经测算,如果将楼房建为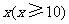 层,则每平方米的平均建筑费用为
层,则每平方米的平均建筑费用为 (单位:元).为了使楼房每平方米的平均综合费用最少,该楼房应建为多少层?
(单位:元).为了使楼房每平方米的平均综合费用最少,该楼房应建为多少层?
(注:平均综合费用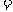 平均建筑费用
平均建筑费用 平均购地费用,平均购地费用
平均购地费用,平均购地费用 )
)
求函数多元参变量的值的主体思路是根据已知条件直接得到参数之间的关系式或者利用导函数条件与图象性质得到特殊关系、然后得方程或方程组求解。而在指定区间内求函数的极值时,则需首先要讨论函数的单调区间,特殊情况还需在给定条件范围内构造新的函数,然后通过讨论新的构造函数的单调性,找到构造函数的增减区间,进而找到该函数的极值点,再求得函数的极值。
例2. (08福建文21). 已知函数 的图像过点(-1,-6),且函数
的图像过点(-1,-6),且函数 的图像关于y轴对称。
的图像关于y轴对称。
(1)求m,n的值及函数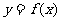 的单调区间;
的单调区间;
(2)若a>0,求函数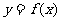 在区间
在区间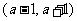 内的极值。
内的极值。
解:(1)由函数f (x)图像过(-1,-6),得m-n=-3,……①
由 ,得:
,得: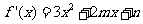
而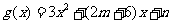 图像关于y轴对称,所以:
图像关于y轴对称,所以: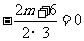 ,即m=-3,
,即m=-3,
代入①得n=0
于是f′(x)=3x2-6x=3x(x-2).
由f′(x)>得x>2或x<0,
故f(x)的单调递增区间是(-∞,0),(2,+∞);
由f′(x)<0得0<x<2,
故f(x)的单调递减区间是(0,2).
(Ⅱ)由(Ⅰ)得f′(x)=3x(x-2),
令f′(x)=0得x=0或x=2.
当x变化时,f′(x)、f(x)的变化情况如下表:
|
X |
(-∞.0) |
0 |
(0,2) |
2 |
(2,+ ∞) |
|
f′(x) |
+ |
0 |
- |
0 |
+ |
|
f(x) |
↗ |
极大值 |
↘ |
极小值 |
↗ |
由此可得:
当0<a<1时,f(x)在(a-1,a+1)内有极大值f(O)=-2,无极小值;
当a=1时,f(x)在(a-1,a+1)内无极值;
当1<a<3时,f(x)在(a-1,a+1)内有极小值f(2)=-6,无极大值;
当a≥3时,f(x)在(a-1,a+1)内无极值.
综上得:当0<a<1时,f(x)有极大值-2,无极小值,当1<a<3时,f(x)有极小值-6,无极大值;当a=1或a≥3时,f(x)无极值.
例3(08湖南理21)已知函数f(x)=ln2(1+x)-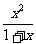 .
.
(I) 求函数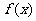 的单调区间;
的单调区间;
(Ⅱ)若不等式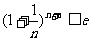 对任意的
对任意的 都成立(其中e是自然对数的底数).
都成立(其中e是自然对数的底数).
求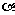 的最大值.
的最大值.
解: (Ⅰ)函数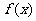 的定义域是
的定义域是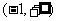 ,
,
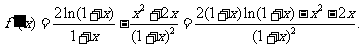
设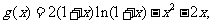 则
则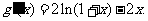
令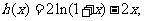 则
则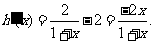
当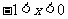 时,
时, 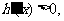
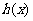 在(-1,0)上为增函数,
在(-1,0)上为增函数,
当x>0时,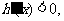
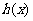 在
在 上为减函数.
上为减函数.
所以h(x)在x=0处取得极大值,而h(0)=0,所以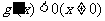 ,
,
函数g(x)在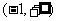 上为减函数.于是当
上为减函数.于是当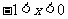 时,
时,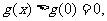
当x>0时,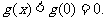
所以,当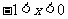 时,
时,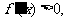
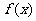 在(-1,0)上为增函数.
在(-1,0)上为增函数.
当x>0时,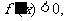
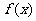 在
在 上为减函数.
上为减函数.
故函数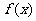 的单调递增区间为(-1,0),单调递减区间为
的单调递增区间为(-1,0),单调递减区间为 .
.
(Ⅱ)不等式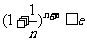 等价于不等式
等价于不等式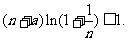 由
由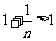 知,
知,
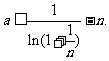 设
设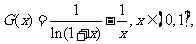 则
则

由(Ⅰ)知,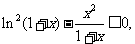 即
即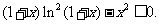
所以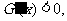
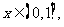 于是G(x)在
于是G(x)在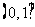 上为减函数.
上为减函数.
故函数G(x)在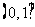 上的最小值为
上的最小值为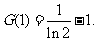
所以a的最大值为
这类题型是2008年命题概率最大的一类,讨论函数的单调区间的解题步骤通常有三步:首先是对函数求导、其次是求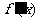 >0或
>0或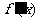 <0的区间,再判断函数的增减性。而求函数参变量的取值范围的解题方法是:想方设法利用求导法建立导函数不等式或不等式组来求解。
<0的区间,再判断函数的增减性。而求函数参变量的取值范围的解题方法是:想方设法利用求导法建立导函数不等式或不等式组来求解。
例1、全国理19.(本小题满分12分)
已知函数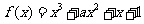 ,
,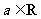 .
.
(Ⅰ)讨论函数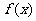 的单调区间;
的单调区间;
(Ⅱ)设函数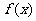 在区间
在区间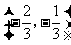 内是减函数,求
内是减函数,求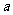 的取值范围.
的取值范围.
解:(1)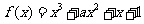 求导:
求导: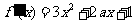
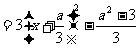
∴当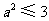 时,得
时,得 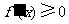 ,
,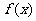 在
在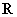 上递增
上递增
而当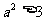 时,
时,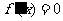 求得两根为
求得两根为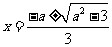
即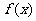 在
在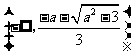 递增,
递增,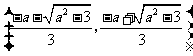 递减,
递减,
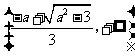 递增
递增
(2)又∵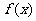 在区间
在区间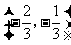 内是减函数,
内是减函数,
∴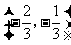

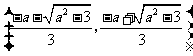
∴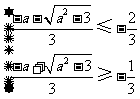 ,且
,且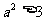 解得:
解得: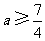
6. station 7. information 8. bookstore 9. helpful 10. left
6.reasonable 7.available 8.different 9.willing 10.reading
(十九) 1When 2 report 3 filled 4 when 5 expectin6 thought 7without
8 threatened 9 jewellery 10 door
(二十)wondering 2. repaired 3. blocks 4. name 5. remember
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com