1．N₁先减小后增大，N₂减小　 2．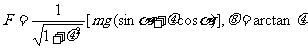

7．要在一张照片上同时拍摄物体正面和几个不同侧面的像，可以在物体的后面放两个直立的大平面镜AO和BO，使物体和它对两个平面镜所成的像都摄入照相机，如图8-17.图中带箭头的圆圈P代表一个人的头部，白色半圆代表人的脸部，此人正面对着照相机的镜头；有斜线的半圆代表脑后的头发；箭头表示头顶上的帽子.图8-17-甲为俯视图. 若两平面镜的夹角∠AOB=72°，设人头的中心恰好位于角平分线OC上，且照相机到人的距离远大于人到平面镜的距离.

(1)试在图8-17-甲画出P的所有的像的位置并用空白和斜线分别表示人脸和头发，以表明各个像的方位.

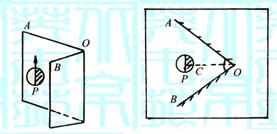
图8-17　　　　　　 图8-17-甲　　　　　 图8-17-乙

(2)在图8-17-乙的方框中画出照片上得到所有的像(分别用空白和斜线表示人脸和头发，用箭头表示头顶上的帽子).

6．如图8-16所示，一储油圆桶，底面直径与桶高均为d.当桶内无油时，从某点A恰能看到桶底边缘上的某点B.当桶内油的深度等于桶高一半时，在A点沿AB方向看去，看到桶底上的C点，C、B相距d/4.由此可得油的折射率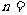　　　　 ；光在油中传播的速度　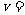　　　 m/s.(结果可用根式表示)

5．F =400N的力拖着小船，使它沿着河中心线运动.现甲、乙两人在河两岸共同拖船，已知甲拉力的方向与河中心线的夹角为30°，要使两人共同产生的效果与F单独作用的效果相同，乙拉力的最小值应为多少？方向如何？

4．一条在湖面上以恒定速度行驶的船上，有一与船固定的竖直光滑墙壁.有一个小球沿水平方向射到墙上. 相对于岸，小球的速度大小为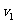，方向与墙的法线成60°角，小球自墙反弹时的速度方向正好与小球入射到墙上时的速度方向垂直.问船的速度应满足什么条件.设小球与墙壁的碰撞是完全弹性的.

3．如图8-15所示，小环m₁、m₂能沿着一轻绳光滑地滑动，绳的两端固定于直杆AB的两端，杆与水平线成角度θ，在此杆上又套一轻小环，绳穿过轻环，并使m₁、m₂在其两边，设环与直杆的接触是光滑的，当系统平衡时，直杆与轻环两边的绳夹角为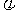，试证：

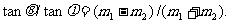
2．一重为G的物块放在倾角为α的斜面上，物块与斜面间的

　 摩擦因数为μ，今在物块上的作用力为F，F可与斜面成

　 任意夹角，如图8-14所示，求拉动物块沿斜面上升所需

　 力F的最小值及对应的θ角.

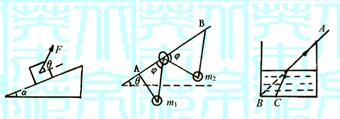　 　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　 图8-13

　　　　　 图8-14　　　　　 图8-15　　　　 图8-16

方法简介

　　　 作图法是根据题意把抽象复杂的物理过程有针对性的表示成物理图像，将物理问题转化成一个几何问题，通过几何知识求解，作图法的优点是直观形象，便于定性分析，也可定性计算，灵活应用作图法会给解题带来很大方便。

赛题精析

　　　 例1　 如图8-1所示，细绳跨过定滑轮，系住一个

质量为m的球，球靠在光滑竖直墙上，当拉动细绳使球

匀速上升时，球对墙的压力将(　　 )

　　　 A．增大　　　　　　　　　 B．先增大后减小　　

　　　 C．减小　　　　　　　　　 D．先减小后增大　　　　　　　　　　　　 图8-1

　　　 解析　 　球在三个力的作用下处于平衡，如图8-1-甲所示.当球上升时，θ角增大，可用动态的三角形定性分析，作出圆球的受力图(如图8-1-甲).从图可见，当球上升时，θ角增大，墙对球的支持力增大，从而球对墙的压力也增大. 故选A正确.

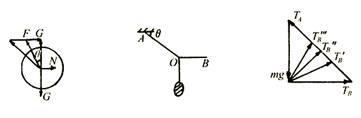
　　　　　　 图8-1-甲　　　　 图8-2　　　　　 图8-2-甲

　　　 例2 　用两根绳子系住一重物，如图8-2所示.绳OA与天花板间夹角θ不变，当用手拉住绳子OB，使绳OB由水平方向转向竖直方向的过程中，OB绳所受的拉力将(　　 )

　　　 A．始终减小　　　　　　　　　　　　　　　　　　　　　 B．始终增大

　　　 C．先减小后增大　　　　　　　　　　　　　　　　　　 D．先增大后减小

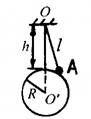　 　　　 解析　 因物体所受重力的大小、方向始终不变，绳OA拉力的方向始终不变，又因为物体始终处于平衡状态，所受的力必然构成一个三角形，如图8-2-甲所示，由图可知OB绳受的拉力是先减小后增大. 可知答案选C

　　　 例3　 如图8-3所示，质量为m的小球A用细绳拴在天花板上，

悬点为O，小球靠在光滑的大球上，处于静止状态.已知：大球的球心

O′在悬点的正下方，其中绳长为l，大球的半径为R，悬点到大球最

高点的距离为h.求对小球的拉力T和小球对大球的压力.

　　　 解析　 力的三角形图和几何三角形有联系，若两个三角形相似，　　　

则可以将力的三角形与几何三角形联系起来，通过边边对应成比例求解.　　　　 图8-3

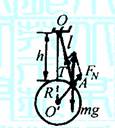　 　　　 以小球为研究对象，进行受力分析，如图8-3-甲所示，小球

受重力mg、绳的拉力T、大球的支持力F_N，其中重力mg与拉力T的

合力与支持力F_N平衡.观察图中的特点，可以看出力的矢量三角形

ABC与几何三角形AOO′相似，即：

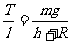
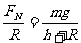
　 　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　图8-3-甲

　　　 所以绳的拉力：T=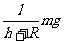

　　　 小球对大球的压力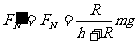

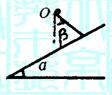　 　　　 例4　 如图8-4所示，质点自倾角为α的斜面上方定点O沿

光滑的斜槽从静止开始下滑，为使质点在最短时间内从O点到达

斜面，斜槽与竖直方向的夹角β应等于多少？

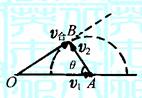
　　　 解析　 如图8-4-甲所示，以经过O点的竖直线上的一点O′

为圆心，OO′为半径作圆，并使该圆与斜面恰好相切于A点，与

OO′延长线交于B点.已知从O点由静止出发沿倾角不同的光滑斜　　　　 图8-4

　 面下滑的质点，到达圆周上不同点所需时间相等，显然，质点沿OA方向从静止开始滑到斜面上所需时间比沿其他方向滑到斜面上所需时间短.

　　　 连接O′A，由几何关系得：

　　　 ∠AO′B=α

　　　 所以所用时间最短时，斜槽与竖直方向的夹角

　　　 β=α/2

　 　　　 所题也可用极限法求解，读者可试试.　　　　　　　　　　　　　　 图8-4-甲

　　　 例5　 一条小河，河水以v₁=5m./s的速度匀速流动，

一条小船在静水中的速度为v₂=4m/s.欲使小船渡河的航

程最短，小船的船头应指向何方向？

　　　 解析　 若v₁< v₂，可垂直渡河，船程最短.但本题

v₁> v₂，小船就不能垂直渡河.但欲使航程最短，则应

使合速度方向与河岸夹角最大.　　　　　　　　　　　　　　　　　　 图8-5

　　　 根据矢量合成的三角形法，v₁、v₂、v_合 ，构成封闭三角形，作图如8-5所示，作有向线段OA表示河水流速v₁，以表示 v₂的有向长度为半径，以A为圆心画圆，过O该圆的切线，切点为B，作有向线段AB，有向线段AB的方向就是所求的方向.由直角三角形AOB，得：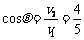

　　　 所以θ=37°

　　　 即小船的船头应指向上游并沿与上游的河岸成37°角的方向.

　 　　　 例6　 一木箱重为G，与地面动摩擦因数为μ，现用斜向

上的力F拉木箱使之沿水平地面匀速前进，如图8-6所示.

求拉力F与水平方向夹角为何值时拉力最小？这个最小值多大？

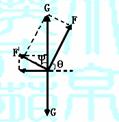
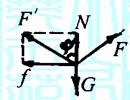
　　　 解析　 木箱受重力G、弹力N、摩擦力f及拉力F四个力

的作用，但此题也可以把木箱看做只受三个力作用，即重力G、　　 　图8-6

拉力F和摩擦力f与支持力N的合力F′，设F′与N的夹角

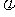　 　 为，则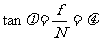，再应用矢量三角形求解　　　　

　　　　　　　　　　　 图8-6-甲　　　　　　　　　 图8-6-乙

　　　 木箱受力情况如图8-6-甲所示，已知G的大小和方向，F′的方向，显然，要使封闭的矢量三角形中F值最小，只有由G的端点作F′的作用线的垂线时，F值最小，如图8-6-乙所示，此时F的最小值为F_min=Gsin()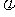

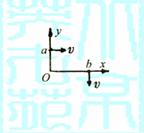　 　　　 其中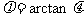，所以最小的拉力F与水平方向的夹角为.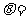

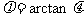　　　 例7 　如图8-7所示，一带电质点，质量为m，电量为q，

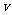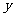以平行于Ox轴的速度从轴上的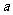点射入图中第一象限所示

的区域，为了使该质点能从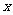轴上的b点以垂直于Ox轴的速度

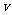射出，可在适当的地方加一个垂直于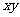平面、磁感应强度为

B的匀强磁场.若此磁场仅分布在一个圆形区域内，试求这圆形

磁场区域的最小半径.重力忽略不计.　　　　　　　　　　　　　　　　 图8-7

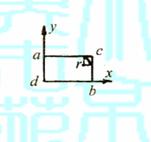　 　　　 解析　 当带电质点以垂直于磁场方向的速度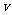进入磁场，在磁场中将做匀速圆周运动，由此要从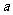点进入从b点射出其圆轨道为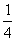圆弧，因而可用作图法求解.

　　　 过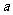点作平行Ox轴的直线，过b作平行Oy的直线，两直线相

交于c点，如图8-7-甲所示，可见只要能保证带电质点的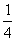圆轨

道处在匀强磁场中，即可使带电质点从b点射出，由此可知，磁场

区域有一最小值，其最小半径为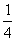圆形轨道两个端点连线的一半，即：　 图8-7-甲

　　　 由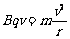可得粒子在磁场中的偏转半径为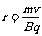

　　　 所加磁场的最小半径为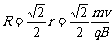

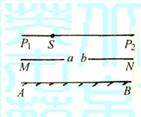　 　　　 例8　 图8-8中AB表示一横放的平面镜，P₁P₂是水平放

置的米尺(有刻度的一面朝着平面镜)，MN是屏，三者互相平

　 行，屏MN上的ab表示一条直缝(即a、b之间是透光的).某　　　　 图8-8

人眼睛紧贴米尺上的小孔S(其位置见图)，可通过平面镜看到

米尺上的一部分刻度.试在本题的图上用三角板作图求出可看到

的部分，并在P₁P₂上把这部分涂以标志　　　 .

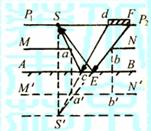
　　　 解析　 根据物像位置镜面对称可知：人眼通过平面镜看到

的米尺刻度范围，好像人眼在平面镜中的像直接去看刻度范围，

不过要受到挡板MN的像M′N′的阻挡，所以先将眼睛在平面　　　 图8-8-甲

镜中成像点S′作出，再作出挡板MN在平面镜中的像M′N′，如图8-8-甲，其中是挡板上的缝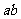在平面镜中的像，连接并延长交AB、P₁P₂于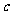、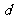两点，再作和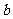的连线交AB于E点，并延长后交P₁P₂于F点，则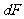即为人眼通过平面镜和挡板后能看到的刻度范围.

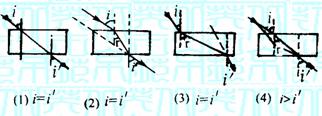
　　　 例9　 光线透过空气中的平行平面厚玻璃板，问下图9-9所示四种情形中哪一种是正确的？

　　　 解析　 根据光的折射定律，光由光疏介质进入光密介质时，光线要向着法线的方向偏析，相反时，向远离法线的方向偏折，且在传播中光路是可逆的.

　　　 由上分析可知，(2)图是正确的.

　　　　　　　　　　　　　 i>r　　　　 i<r　　　　 　i>r

图8-9

方法简介

3.《交变电流》板书照片