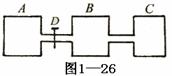
11．如图1-26所示，A 、B 、C三个容器内装有同种气体，已知V_A = V_B = 2L ，V_C = 1L ，T_A = T_B = T_C = 300K ，阀门D关闭时p_A = 3atm ，p_B = p_C = 1atm 。若将D打开，A中气体向B 、C迁移(迁移过程中温度不变)，当容器A中气体压强降为P_a′= 2atm时，关闭D ；然后分别给B 、C加热，使B中气体温度维持T_b′= 400K ，C中气体温度维持T_c′= 600K ，求此时B 、C两容器内气体的压强(连通三容器的细管容积不计)。

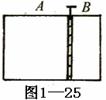
10．用销钉固定的活塞把水平放置的容器分隔成A 、B两部分，其体　　　 积之比V_A ∶V_B = 2∶1 ，如图1-25所示。起初A中有温度为127℃ ，压强为1.8×10⁵Pa的空气，B中有温度27℃ ，压强为1.2×10⁵Pa的空气。拔出销钉，使活塞可以无摩擦地移动(不漏气)。由于容器缓慢导热，最后气体都变成室温27℃ ，活塞也停住，求最后A中气体的压强。

9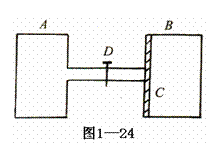．如图1-24所示，A 、B是体积相同的气缸，B内有一导热的、可在气缸内无摩擦滑动的、体积不计的活塞C 、D为不导热的阀门。起初，阀门关闭，A内装有压强P₁ = 2.0×10⁵Pa ，温度T₁ = 300K的氮气。B内装有压强P₂ = 1.0×10⁵Pa ，温度T₂ = 600K的氧气。阀门打开后，活塞C向右移动，最后达到平衡。以V₁和V₂分别表示平衡后氮气和氧气的体积，则V₁∶V₂ =　　　　 。(假定氧气和氮气均为理想气体，并与外界无热交换，连接气体的管道体积可忽略)

8．如图2-23所示，一质量为M ，长为l的长方形木板B ，放在光滑的水平地面上，在其右端放一质量为m的小木块，且m＜M 。现以地面为参考系，给A和B以大小相等、方向相反的初速度，使A开始向左运动，B开始向右运动，且最后A没有滑离木板B，求以地面为参考系时小木块A的最大位移是多少？摩擦力做的功是多大？

7．如图1-22所示，水平转盘绕竖直轴OO′转动，两木块质量分别为M与m ，到轴线的距离分别是L₁和L₂ ，它们与转盘间的最大静摩擦力为其重力的μ倍，当两木块用水平细绳连接在一起随圆盘一起转动并不发生滑动时，转盘最大角速度可能是多少？

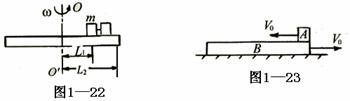
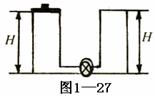
6．如图1-21所示，AB和CD为两个斜面，其上部足够长，下部分别与一光滑圆弧面相切，EH为整个轨道的对称轴，圆弧所对圆心角为120°，半径为2m ，某物体在离弧底H高h = 4m处以V₀ = 6m/s沿斜面运动，物体与斜面的摩擦系数μ = 0.04 ，求物体在AB与CD两斜面上(圆弧除外)运动的总路程。(取g = 10m/s²)

5．如图1-20所示为一个横截面为半圆，半径为R的光滑圆柱，一根不可伸长的细绳两端分别系着小球A 、B ，且m_A = 2m_B ，由图示位置从静止开始释放A球，当小球B达到半圆的顶点时，求线的张力对小球A所做的功。

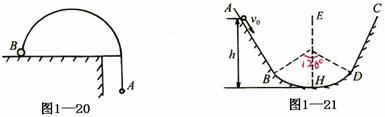
4．如图1-19，一质量为M的长木板静止在光滑水平桌面上。一质量为m的小滑块以水平速度v₀从长木板的一端开始在木板上滑动，直到离开木板。滑块刚离开木板时的速度为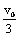。若把该木板固定在水平桌面上，其他条件相同，求滑决离开木板时的速度v 。

3．质量为m的运动员站在质量为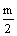的均匀长板AB的中点，板位于水平面上，可绕通过B点的水平轴转动，板的A端系有轻绳，轻绳的另一端绕过两个定滑轮后，握在运动员手中。当运动员用力拉绳时，滑轮两侧的绳子都保持在竖直方向，如图1-18所示。要使板的A端离开地面，运动员作用于绳子的最小拉力是　　　　 。

2．一粒钢珠从静止状态开始自由下落，然后陷入泥潭中，若把在空中下落的过程称为过程I ，进入泥潭直到停止的过程称为过程II ，则(　　 )

A、过程I中钢珠动量的改变量等于它重力的冲量

B、过程II中阻力的冲量的大小等于全过程中重力冲量的大小

C、过程II中钢珠克服阻力所做的功等于过程I与过程II中钢珠所减少的重力势能之和

D、过程II中损失的机械能等于过程I中钢珠所增加的动能