
4.下列各句中,标点符号的运用正确的一句是( )
A.十七大报告突出强调,“确保权力正确行使,必须让权力在阳光下运行”,这反映了中国共产党在权力运行上更加公开、公平、公正的坚强决心。
B.就考核制度来讲,考核前,一次特别安排的游乐活动或会餐,往往起到“堵嘴”的作用。考核中,只有被考核人滔滔不绝地“摆功”,没有提问,没有质询。
C.11月21日,在网络歌手杨臣刚和农村留守儿童合唱的“八荣八耻,和谐中国”主题曲歌声中,“万映计划万企联动”慈善盛典系列活动正式启动。
D.丹麦前驻华大使的夫人、研究汉阙的专家燕妮·帕尔感慨地说:“我在北京看了许多图片、文字资料,没想到这块汉阙竟是这样精美?”
3.下面各句中,加点词语使用恰当的一项是( )
A.他的音质很好,可惜师出无名,如果能有名师指点,他在音乐上肯定会有光明的前途。
B.平儿明知是谁偷了茯苓霜,但投鼠忌器,怕伤了那主人探春的体面,所以不愿去起赃。
C.科学研究中,在同一现象面前,粗心的人不以为然,或视而不见;细心的人则抓住不放,以此为追求新发现的端倪。
D.今天的主题讨论,各组角度不同,因而侧重各异,如此南辕北辙,怎么能达成协议呢?
2.依次填入下列各句横线处的词语,最恰当的一组是( )
①自南北朝以来日益兴盛的佛教,特别是经过武则天的 ,确实达到了发展的最高峰。
②一般而言,年轻人对流行歌曲会有更多的兴趣,而老年人在这方面就要了。
③最近,MSN服务将要收费的消息在媒体和用户中流传。微软在华的MSN负责人告诉记者,这是由中美商业模式差别造成的 ,基于个人计算机的MSN将 免费下去。
A.扶持 淡薄 误解/一直 B.扶植 淡泊 曲解/始终
c.扶持 淡泊 曲解/始终 D.扶植 淡薄 误解/一直
1.下列各项中,字音、字形全对的一项是( )
A.扁(biǎn)担 扁(piān)舟 伯(bó)仲 大伯(bǎi)子
B.倘(tǎng)或 嗔(chēn)视 数(shuò)见不鲜 千乘(shèng)之国
C.揣(chuāi)手儿 挣揣(chuài) 监(jiān)生 太监(jiàn狐)
D.碑帖(tiě) 病殁(mò) 隽(juàn)语箴言 有的(dì)放矢.
7.(本小题满分14分)
已知函数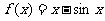
(Ⅰ)若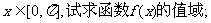
(Ⅱ)若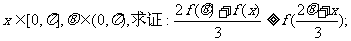
(Ⅲ)若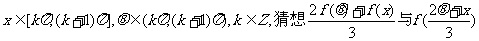 的大小关系(不必写出比较过程).
的大小关系(不必写出比较过程).
解:(Ⅰ)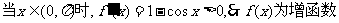

(Ⅱ)设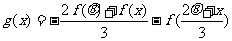 ,
,
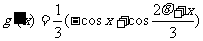 ……6分
……6分
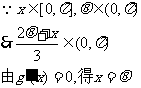

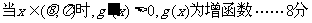

(Ⅲ)在题设条件下,当k为偶数时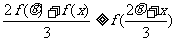
当k为奇数时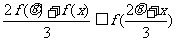 ……14分
……14分
6.(本小题满分12分)
垂直于x轴的直线交双曲线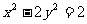 于M、N不同两点,A1、A2分别为双曲线的左顶点和右顶点,设直线A1M与A2N交于点P(x0,y0)
于M、N不同两点,A1、A2分别为双曲线的左顶点和右顶点,设直线A1M与A2N交于点P(x0,y0)
(Ⅰ)证明:
(Ⅱ)过P作斜率为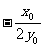 的直线l,原点到直线l的距离为d,求d的最小值.
的直线l,原点到直线l的距离为d,求d的最小值.
解(Ⅰ)证明: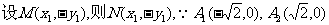
 ①
①
直线A2N的方程为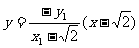 ②……4分
②……4分
①×②,得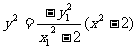

(Ⅱ)
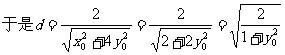 ……10分
……10分
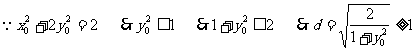
当 ……12分
……12分
5.(本小题满分14分)
(理)给定正整数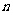 和正数
和正数 ,对于满足条件
,对于满足条件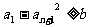 的所有无穷等差数列
的所有无穷等差数列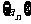 ,试求
,试求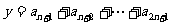 的最大值,并求出
的最大值,并求出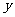 取最大值时
取最大值时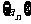 的首项和公差.
的首项和公差.
(文)给定正整数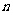 和正数
和正数 ,对于满足条件
,对于满足条件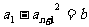 的所有无穷等差数列
的所有无穷等差数列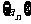 ,试求
,试求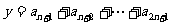 的最大值,并求出
的最大值,并求出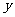 取最大值时
取最大值时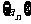 的首项和公差.
的首项和公差.
(理)解:设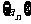 公差为
公差为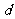 ,则
,则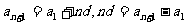 . 3分
. 3分
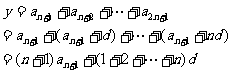
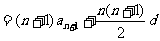 4分
4分

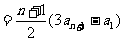 . 7分
. 7分
又 .
.
∴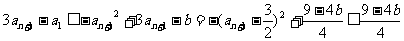 ,当且仅当
,当且仅当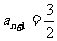 时,等号成立. 11分
时,等号成立. 11分
∴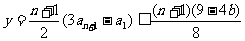 . 13分
. 13分
当数列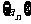 首项
首项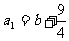 ,公差
,公差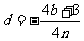 时,
时,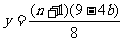 ,
,
∴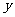 的最大值为
的最大值为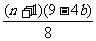 . 14分
. 14分
(文)解:设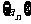 公差为
公差为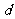 ,则
,则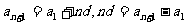 . 3分
. 3分
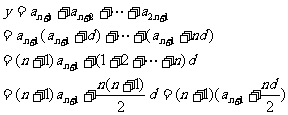
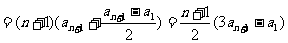 , 6分
, 6分
又 .
.
∴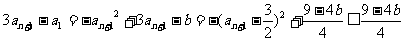 .
.
当且仅当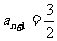 时,等号成立. 11分
时,等号成立. 11分
∴ . 13分
. 13分
当数列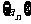 首项
首项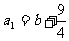 ,公差
,公差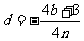 时,
时,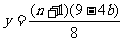 .
.
∴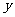 的最大值为
的最大值为 . 14分
. 14分
4.(本小题满分12分)
设椭圆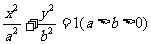 的左焦点为
的左焦点为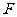 ,上顶点为
,上顶点为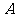 ,过点
,过点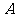 与
与 垂直的直线分别交椭圆和
垂直的直线分别交椭圆和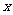 轴正半轴于
轴正半轴于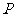 ,
,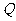 两点,且
两点,且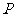 分向量
分向量 所成的比为8∶5.
所成的比为8∶5.
(1)求椭圆的离心率;
(2)若过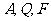 三点的圆恰好与直线
三点的圆恰好与直线 :
: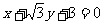 相切,求椭圆方程.
相切,求椭圆方程.
解:(1)设点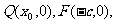 其中
其中 .
.
由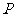 分
分 所成的比为8∶5,得
所成的比为8∶5,得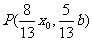 , 2分
, 2分
∴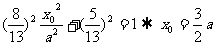 .①, 4分
.①, 4分
而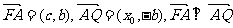 ,
,
∴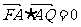 .
.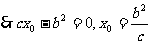 .②, 5分
.②, 5分
由①②知 .
.
∴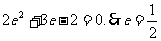 . 6分
. 6分
(2)满足条件的圆心为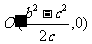 ,
,
 , 8分
, 8分
圆半径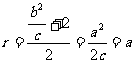 . 10分
. 10分
由圆与直线 :
: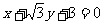 相切得,
相切得,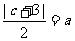 ,
,
又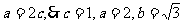 .∴椭圆方程为
.∴椭圆方程为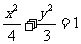 . 12分
. 12分
3. (本小题满分13分)
已知数列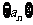 的前n项和为
的前n项和为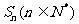 ,且
,且 对任意自然数都成立,其中m为常数,且
对任意自然数都成立,其中m为常数,且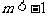 .
.
(I)求证数列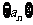 是等比数列;
是等比数列;
(II)设数列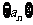 的公比
的公比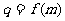 ,数列
,数列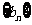 满足:
满足: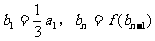
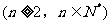 ,试问当m为何值时,
,试问当m为何值时,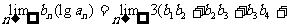
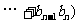 成立?
成立?
解:(I)由已知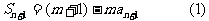
 (2)
(2)
由 得:
得: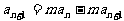 ,即
,即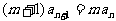 对任意
对任意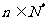 都成立
都成立

(II)当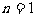 时,
时,

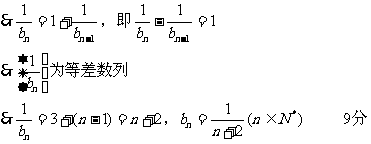
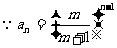
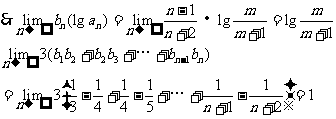
由题意知 ,
,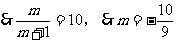 13分
13分
19. (本小题满分14分)
设双曲线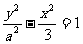 的两个焦点分别为
的两个焦点分别为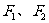 ,离心率为2.
,离心率为2.
(I)求此双曲线的渐近线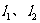 的方程;
的方程;
(II)若A、B分别为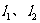 上的点,且
上的点,且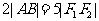 ,求线段AB的中点M的轨迹方程,并说明轨迹是什么曲线;
,求线段AB的中点M的轨迹方程,并说明轨迹是什么曲线;
(III)过点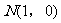 能否作出直线
能否作出直线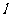 ,使
,使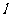 与双曲线交于P、Q两点,且
与双曲线交于P、Q两点,且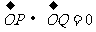 .若存在,求出直线
.若存在,求出直线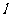 的方程;若不存在,说明理由.
的方程;若不存在,说明理由.
解:(I)
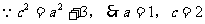
 ,渐近线方程为
,渐近线方程为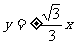 4分
4分
(II)设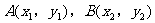 ,AB的中点
,AB的中点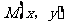

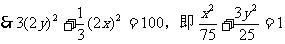
则M的轨迹是中心在原点,焦点在x轴上,长轴长为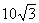 ,短轴长为
,短轴长为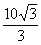 的椭圆.(9分)
的椭圆.(9分)
(III)假设存在满足条件的直线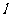
设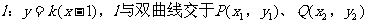


由(i)(ii)得
∴k不存在,即不存在满足条件的直线 . 14分
. 14分
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com