
40.(2009常州中学月考) 跳水是一项优美的水上运动,如图甲是2008年北京奥运会跳水比赛中小将陈若琳和王鑫在跳台上腾空而起的英姿。其中陈若琳的体重约为30 kg,身高约为1.40m,她站在离水面10m高的跳台上,重心离跳台面的高度约为0.80m,竖直向上跃起后重心升高0.45m达到最高点,入水时身体竖直,当手触及水面时伸直双臂做一个翻掌压水花的动作,如图13乙所示,这时陈若琳的重心离水面约为0.80m。设运动员在入水及在水中下沉过程中受到的水的作用力大小不变。空气阻力可忽略不计,重力加速度g取10m/s2。(结果保留2位有效数字)
(1)求陈若琳从离开跳台到手触及水面的过程中可用于完成一系列动作的时间;
(2)若陈若琳入水后重心下沉到离水面约2.2m处速度变为零,试估算水对陈若琳的阻力的大小。

答案:(1)陈若琳跃起后可看作竖直向上的匀减速运动,重心上升的高度h1=0.45m
设起跳速度为v0,则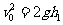 ,上升过程的时间
,上升过程的时间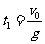
解得 t1=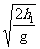 =0.3 s
=0.3 s
陈若琳从最高处自由下落到手触及水面的过程中重心下落的高度h=10.45m
设下落过程的时间为t2,则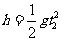
解得 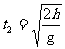 =
=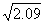 s≈1.4 s
s≈1.4 s
陈若琳要完成一系列动作可利用的时间t=t1+t2=1.7s
说明:t2用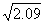 s表示也给分。
s表示也给分。
(2)陈若琳的手触及水面到她的重心下沉到离水面约2.2m处的位移s=3.0 m
手触及水面时的瞬时速度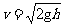
设水对运动员的作用力为Ff,依据动能定理有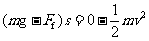
解得 Ff=1.3´103N
说明:用其他方法求解,正确的也给分
39.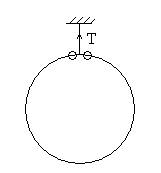 (巢湖市六中2008-2009学年度高三第一次月考)质量为M的圆环用细线(质量不计)悬挂着,将两个质量均为m的有孔小珠套在此环上且可以在环上做无摩擦的滑动,如图所示,今同时将两个小珠从环的顶部释放,并沿相反方向自由滑下,试求:
(巢湖市六中2008-2009学年度高三第一次月考)质量为M的圆环用细线(质量不计)悬挂着,将两个质量均为m的有孔小珠套在此环上且可以在环上做无摩擦的滑动,如图所示,今同时将两个小珠从环的顶部释放,并沿相反方向自由滑下,试求:
(1)在圆环不动的条件下,悬线中的张力T随cosθ(θ为小珠和大环圆心连线与竖直方向的夹角)变化的函数关系,并求出张力T的极小值及相应的cosθ值;
(2)小球与圆环的质量比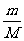 至少为多大时圆环才有可能上升?
至少为多大时圆环才有可能上升?
答案 (1)每个小珠受重力mg和支持力N作用,小珠在θ处有: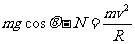
机械能守恒: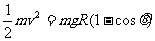 得:
得: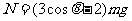
对环分析得:
 即:
即: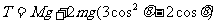
当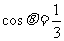 (即
(即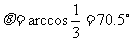 )时:
)时: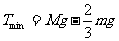
(2)由上面得到的N的表达式知,当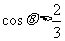 时,N>0,为压力;只有当
时,N>0,为压力;只有当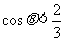 时,N<0,为拉力,这是圆环上升的必要条件。圆环上升的条件是T≤0,即:
时,N<0,为拉力,这是圆环上升的必要条件。圆环上升的条件是T≤0,即: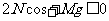 临界状态为
临界状态为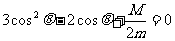
上式有实根的条件为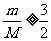
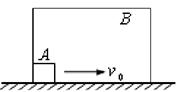
38. (肥西中学高三物理第二次月考试卷)如图所示,质量均为m的物块A和B用弹簧连结起来,将它们悬于空中静止,弹簧处于原长状态,A距地面高度H=0.90m,同时释放两物块,A与地面碰撞后速度立即变为零,由于B的反弹,A刚好能离开地面。若B物块换为质量为2m的物块C(图中未画出),仍将它们悬于空中静止且弹簧为原长,从A距地面高度为H’处同时释放,设A也刚好能离开地面。已知弹簧的弹性势能EP与弹簧的劲度系数k和形变量x的关系是:EP=kx2。试求:(1)B反弹后,弹簧的最大伸长量。(2)H’的大小
(肥西中学高三物理第二次月考试卷)如图所示,质量均为m的物块A和B用弹簧连结起来,将它们悬于空中静止,弹簧处于原长状态,A距地面高度H=0.90m,同时释放两物块,A与地面碰撞后速度立即变为零,由于B的反弹,A刚好能离开地面。若B物块换为质量为2m的物块C(图中未画出),仍将它们悬于空中静止且弹簧为原长,从A距地面高度为H’处同时释放,设A也刚好能离开地面。已知弹簧的弹性势能EP与弹簧的劲度系数k和形变量x的关系是:EP=kx2。试求:(1)B反弹后,弹簧的最大伸长量。(2)H’的大小
答案:(1)A落地时,B的速度为
υB= ①
设反弹后上升的最大高度为x,
A恰好离开地面时 kx=mg ②
由系统机械能守恒 mυB2=mgx+kx2 ③
由①②③联立得 x=0.6m
(2)将B换成C后,A落地时,C的速度为 υC=
C反弹后上升到最高时A刚好离开地面, 故仍有 kx=mg
由系统机械能守恒
1/2·2mυc2=2mgx+kx2 解得:H’=0.75m
37.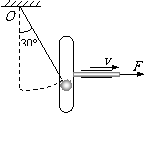 (2009高淳外校月考) 如图所示,轻且不可伸长的细绳悬挂质量为0.5kg 的小圆球,圆球又套在可沿水平方向移动的框架槽内,框架槽沿铅直方向,质量为0.2kg.自细绳静止于铅直位置开始,框架在水平力F=20N恒力作用下移至图中位置,此时细绳与竖直方向夹角30°.绳长0.2m,不计一切摩擦.
(2009高淳外校月考) 如图所示,轻且不可伸长的细绳悬挂质量为0.5kg 的小圆球,圆球又套在可沿水平方向移动的框架槽内,框架槽沿铅直方向,质量为0.2kg.自细绳静止于铅直位置开始,框架在水平力F=20N恒力作用下移至图中位置,此时细绳与竖直方向夹角30°.绳长0.2m,不计一切摩擦.
求:(1)此过程中重力对小圆球做功为多少?
(2)外力F做功为多大?
(3)小圆球在此位置的瞬时速度大小是多少.(取g=10m/s2)
答案(1)小球重力所做功为
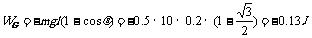
(2)外力F做功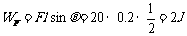
(3)将小球和框架槽看作一个系统,则系统动能定理: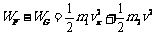
其中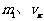 为小球的质量和小球此时的速度,
为小球的质量和小球此时的速度,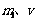 为框架槽的质量和此时的速度.
为框架槽的质量和此时的速度.
由运动的分解得: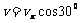
代入上述方程::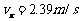
36.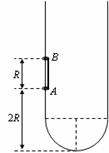 (2009江浦中学月考) 光滑的长轨道形状如图所示,底部为半圆型,半径R,固定在竖直平面内。AB两质量相同的小环用长为R的轻杆连接在一起,套在轨道上。将AB两环从图示位置静止释放,A环离开底部2R。不考虑轻杆和轨道的接触,即忽略系统机械能的损失,求:
(2009江浦中学月考) 光滑的长轨道形状如图所示,底部为半圆型,半径R,固定在竖直平面内。AB两质量相同的小环用长为R的轻杆连接在一起,套在轨道上。将AB两环从图示位置静止释放,A环离开底部2R。不考虑轻杆和轨道的接触,即忽略系统机械能的损失,求:
(1)AB两环都未进入半圆型底部前,杆上的作用力。
(2)A环到达最低点时,两球速度大小。
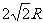 (3)若将杆换成长
,A环仍从离开底部2R处静止释放,经过半圆型底部再次上升后离开底部的最大高度
。
(3)若将杆换成长
,A环仍从离开底部2R处静止释放,经过半圆型底部再次上升后离开底部的最大高度
。
答案⑴ 对整体自由落体,加速度为g; 以A为研究对象,A作自由落体则杆对A一定没有作用力。
⑵ AB都进入圆轨道后,两环具有相同角速度,则两环速度大小一定相等
整体机械能守恒: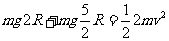
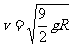
⑶ A再次上升后,位置比原来高h,如图所示。
由动能定理 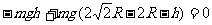
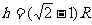 ,
,
A离开底部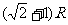
35.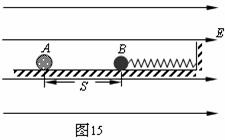 (2009广东省茂名市模拟) 如图15所示,劲度系数为k的轻弹簧,左端连着绝缘介质小球B,右端连在固定板上,放在光滑绝缘的水平面上。整个装置处在场强大小为E、方向水平向右的匀强电场中。现有一质量为m、带电荷量为+q的小球A,从距B球为S处自由释放,并与B球发生碰撞。碰撞中无机械能损失,且A球的电荷量始终不变。已知B球的质量M=3m,B球被碰后作周期性运动,其运动周期
(2009广东省茂名市模拟) 如图15所示,劲度系数为k的轻弹簧,左端连着绝缘介质小球B,右端连在固定板上,放在光滑绝缘的水平面上。整个装置处在场强大小为E、方向水平向右的匀强电场中。现有一质量为m、带电荷量为+q的小球A,从距B球为S处自由释放,并与B球发生碰撞。碰撞中无机械能损失,且A球的电荷量始终不变。已知B球的质量M=3m,B球被碰后作周期性运动,其运动周期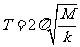 (A、B小球均可视为质点)。
(A、B小球均可视为质点)。
(1)求A球与B球第一次碰撞后瞬间,A球的速度V1和B球的速度V2;
(2)要使A球与B球第二次仍在B球的初始位置迎面相碰,求劲度系数k的可能取值。
答案:(1)设A球与B球碰撞前瞬间的速度为v0,
由动能定理得, 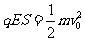 ①
①
解得:
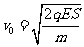 ②
②
碰撞过程中动量守恒
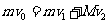 ③
③
机械能无损失,有 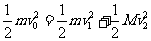 ④
④
解得
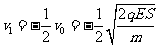 负号表示方向向左
负号表示方向向左
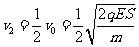 方向向右
方向向右
(2)要使m与M第二次迎面碰撞仍发生在原位置,则必有A球重新回到O处所用 的时间t恰好等于B球的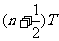
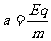 ⑥
⑥
 (n=0 、1 、2 、3 ……) ⑦
(n=0 、1 、2 、3 ……) ⑦
由题意得: 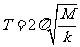 ⑧
⑧
解得: 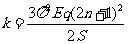 (n=0 、1 、2 、3 ……) ⑨
(n=0 、1 、2 、3 ……) ⑨
34.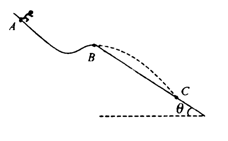 (2009南阳中学月考) 如图所示,质量m=60kg的高山滑雪运动员,从A点由静止开始沿滑雪道滑下,从B点水平飞出后又落在与水平面成倾角
(2009南阳中学月考) 如图所示,质量m=60kg的高山滑雪运动员,从A点由静止开始沿滑雪道滑下,从B点水平飞出后又落在与水平面成倾角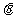 =
=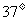 的斜坡上C点.已知AB两点间的高度差为h=25m,B、C两点间的距离为s=75m,已知sin370=0.6,取g=10m/s2,求:
的斜坡上C点.已知AB两点间的高度差为h=25m,B、C两点间的距离为s=75m,已知sin370=0.6,取g=10m/s2,求:
(1)运动员从B点水平飞出时的速度大小;
(2)运动员从A点到B点的过程中克服摩擦力做的功.
解:(1)由B到C平抛运动的时间为t
竖直方向:hBc=ssin37o= gt2 (1)
gt2 (1)
水平方向:scos370=vBt (2)
代得数据,解(1)(2)得vB=20m/s (3)
(2)A到B过程,由动能定理有
mghAB+wf= mvB2 (4)
mvB2 (4)
代人数据,解(3)(4)得 wf =-3000J
所以运动员克服摩擦力所做的功为3000J
33.(2009东城区期末试题) 如图所示,在距水平地面高h=0.80m的水平桌面一端的边缘放置一个质量m=0.80kg的木块B,桌面的另一端有一块质量M=1.0kg的木块A以初速度v0=4.0m/s开始向着木块B滑动,经过时间t=0.80s与B发生碰撞,碰后两木块都落到地面上。木块B离开桌面后落到地面上的D点。设两木块均可以看作质点,它们的碰撞时间极短,且已知D点距桌面边缘的水平距离s=0.60m,木块A与桌面间的动摩擦因数μ=0.25,重力加速度取g=10m/s2。求:

(1)两木块碰撞前瞬间,木块A的速度大小;
(2)木块B离开桌面时的速度大小;
(3)木块A落到地面上的位置与D点之间的距离。
答案:(1)木块A在桌面上受到滑动摩擦力作用做匀减速运动,根据牛顿第二定律,木块A的加速度 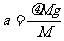 =2.5m/s2
=2.5m/s2
设两木块碰撞前A的速度大小为v,根据运动学公式,得
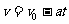 =2.0m/s…
=2.0m/s…
(2)两木块离开桌面后均做平抛运动,设木块B离开桌面时的速度大小为v2,在空中飞行的时间为t′。根据平抛运动规律有: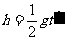 ,s=v2t′
,s=v2t′
解得:
 =1.5m/s
=1.5m/s
(3)设两木块碰撞后木块A的速度大小为v1,根据动量守恒定律有:
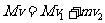
解得:
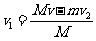 =0.80m/s
=0.80m/s
设木块A落到地面过程的水平位移为s′,根据平抛运动规律,得
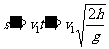 =0.32m
=0.32m
则木块A落到地面上的位置与D点之间的距离 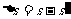 =0.28m
=0.28m
32. (2009年广东省实验中学模拟)如图所示,矩形盒
(2009年广东省实验中学模拟)如图所示,矩形盒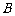 的质量为
的质量为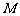 ,底部长度为
,底部长度为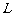 ,放在水平面上,盒内有一质量为
,放在水平面上,盒内有一质量为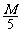 可视为质点的物体
可视为质点的物体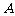 ,
,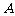 与
与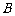 、
、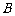 与地面的动摩擦因数均为
与地面的动摩擦因数均为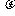 ,开始时二者均静止,
,开始时二者均静止,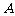 在
在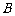 的左端。现瞬间使物体
的左端。现瞬间使物体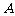 获得一向右的水平初速度
获得一向右的水平初速度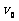 ,以后物体
,以后物体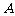 与盒
与盒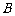 的左右壁碰撞时,
的左右壁碰撞时,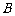 始终向右运动。当
始终向右运动。当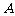 与
与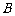 的左壁最后一次碰撞后,
的左壁最后一次碰撞后,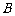 立刻停止运动,
立刻停止运动,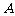 继续向右滑行
继续向右滑行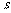 (
(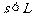 )后也停止运动。
)后也停止运动。
(1)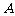 与
与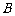 第一次碰撞前,
第一次碰撞前,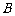 是否运动?
是否运动?
(2)若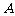 第一次与
第一次与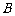 碰后瞬间向左运动的速率为
碰后瞬间向左运动的速率为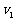 ,求此时矩形盒
,求此时矩形盒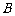 的速度大小
的速度大小
(3)当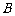 停止运动时,
停止运动时,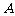 的速度是多少?
的速度是多少?
答案 (1) 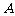 与
与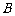 第一次碰撞前,A、B之间的压力等于A的重力,即
第一次碰撞前,A、B之间的压力等于A的重力,即
A对B的摩擦力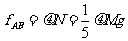
而B与地面间的压力等于A、B重力之和,即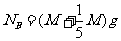
地面对B的最大静摩擦力 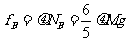
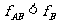 故
故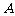 与
与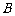 第一次碰撞前,B不运动
第一次碰撞前,B不运动
(2)设A第一次碰前速度为v,碰后B的速度为v2
则由动能定理有
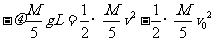 …
…
碰撞过程中动量守恒
有 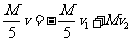
解得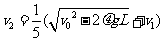
(3)当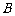 停止运动时,
停止运动时, 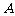 继续向右滑行
继续向右滑行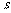 (
(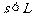 )后停止,设B停止时,
)后停止,设B停止时,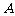 的速度为
的速度为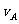 ,则由动能定理…
,则由动能定理…
得
 …
…
解得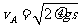
31.(2009年深圳一模) 光滑水平面上有两个小木块A和B,其质量mA=1kg、mB=4kg,它们中间用一根轻质弹簧相连.一颗水平飞行的子弹质量为m=50g,以V0=500m/s的速度在极短时间内射穿两木块,已知射穿A木块后子弹的速度变为原来的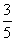 ,且子弹射穿A木块损失的动能是射穿B木块损失的动能的2倍.求:系统运动过程中弹簧的最大弹性势能.
,且子弹射穿A木块损失的动能是射穿B木块损失的动能的2倍.求:系统运动过程中弹簧的最大弹性势能.
答案 弹穿过A时,子弹与A动量守恒,
由动量守恒定律: ……………………… ①
而由 得:v1=300m/s
得: ………………………②
子弹穿过B时, 子弹与B动量守恒,
由动量守恒定律: ………………………③
又由 …………………④
得:v2=100m/s
由③,④得: ………………………⑤
子弹穿过B以后,弹簧开始被压缩,A、B和弹簧所组成的系统动量守恒
由动量守恒定律: ………………………⑥
由能量关系: ……………………⑦
由② ⑤ ⑥ ⑦得: ………………………⑧
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com