
2、已知函数f(x)=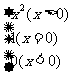
求f(1),f[f(-3)],f{f[f(-3)]}的值.
答案:1;1;1。
例3、已知函数f(x)=2x2-2ax+3在区间[-1,1]上有最小值,记作g(a).
(1)求g(a)的函数表达式
(2)求g(a)的最大值。
[解]:
对称轴x=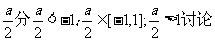
得g(a)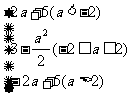
利用分段函数图象易得:g(a)max=3
点评:二次函数在闭区间上的最值问题往往结合图象讨论。
追踪训练
1、设函数f(x)=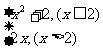 则f(-4)=___________,若f(x0)=8,则x0=________
则f(-4)=___________,若f(x0)=8,则x0=________
答 案:18;
案:18;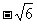 或4。
或4。
例2、某同 学从甲地以每小时6千米的速度步行2小时到达乙地,在乙
学从甲地以每小时6千米的速度步行2小时到达乙地,在乙 地耽搁
地耽搁 1小时后,又以每小时4千米的速
1小时后,又以每小时4千米的速 度步行返回甲地。写出该同学在上述过程中,离甲地的距离S(千米)和时间t(小时)的函数关系式,并作出函数图象。
度步行返回甲地。写出该同学在上述过程中,离甲地的距离S(千米)和时间t(小时)的函数关系式,并作出函数图象。
[解]:
先考虑由甲地到乙地的过程:
0≤t≤2时, y=6t
再考虑在乙地耽搁的情况:
2<t≤3时, y=12
最后考虑由乙地返回甲地的过程:
3<t≤6时, y=12-4(t-3)
所以S(t)=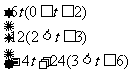
函数图象(略)
点评:某些实际问题的函数解析式常用分段函数表示,须针对自变量的分段变化情况,列出各段不同的解析式,再依据自变量的不同取值范围,分段画出函数的图象.
例1、已知函数y=|x-1|+|x+2|
(1)作出函数的图象。
(2)写出函数的定义域和值域。
[解]:
(1)首先考虑去掉解析式中的绝对值符号,第一个绝对值的分段点x=1,第二个绝对值的分段点x=-2,这样数轴被分为三部分:(-∞,-2],(-2,1],(1,+∞)
所以已知函数可写为分段函数形式:
y=|x-1|+|x+2|=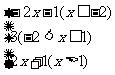
在相应的x取值范围内,分别作出相应函数的图象,即为所求函数的图象。(图象略)
(2)根据函数的图象可知:函数的定义域为R,值域为 [3,+∞)
[3,+∞)
21、设函数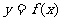 是定义在
是定义在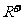 上的减函数,并且满足
上的减函数,并且满足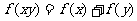 ,
,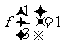 ,
,
(1)求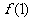 的值, (2)如果
的值, (2)如果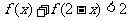 ,求x的取值范围。(16分)
,求x的取值范围。(16分)
20、对于二次函数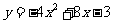 ,(16分)
,(16分)
(1)指出图像的开口方向、对称轴方程、顶点坐标;
(2)画出它的图像,并说明其图像由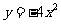 的图像经过怎样平移得来;
的图像经过怎样平移得来;
(3)求函数的最大值或最小值;
(4)分析函数的单调性。
19、证明:函数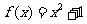 是偶函数,且在
是偶函数,且在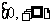 上是增加的。(14分)
上是增加的。(14分)

18、已知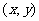 在映射
在映射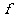 的作用下的像是
的作用下的像是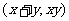 ,求
,求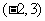 在
在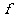 作用下的像和
作用下的像和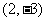 在
在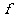 作用下的原像。(12分)
作用下的原像。(12分)
17、求下列函数的定义域:(12分)
(1) (2)
(2)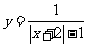
16、设 ,若
,若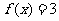 ,则
,则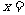 。
。
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com