
4、 周期性:解决抽象函数的周期性问题--充分理解与运用相关的抽象式是关键。
材料四:设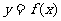 是定义在R上的奇函数,其图象关于直线
是定义在R上的奇函数,其图象关于直线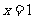 对称。证明
对称。证明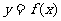 是周期函数。
是周期函数。
证明:由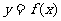 的图象关于直线
的图象关于直线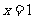 对称,得
对称,得 ,
,
又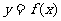 是定义在R上的奇函数,所以
是定义在R上的奇函数,所以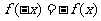
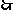
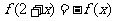 ,则
,则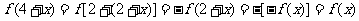
由周期函数的定义可知4是它的一个周期。
总结:
 一般地,
一般地, ,
,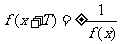 均可断定函数的周期为2T。
均可断定函数的周期为2T。
3、 对称性:解决抽象函数的对称问题--定义证明是根本、图象变换是 捷径、特值代入是妙法。
捷径、特值代入是妙法。
材料三:设函数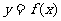 定义在实数集上,则函数
定义在实数集上,则函数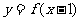 与
与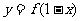 的图象关于( )
的图象关于( )
A、直线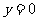 对称 B直线
对称 B直线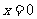 对称 C直线
对称 C直线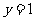 对称 D直线
对称 D直线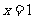 对称
对称
解法一(定义证明):设点 是函数
是函数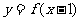 的图象上的任意一点
的图象上的任意一点 ,则
,则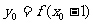 ,
, 关于直线
关于直线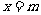 的对称点为
的对称点为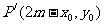 ,要使点
,要使点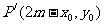 在函数
在函数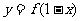 的图象上,则
的图象上,则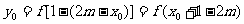 ,应有
,应有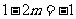 ,故
,故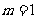 ,
,
 所以函数
所以函数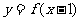 与
与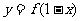 的图象关于直线
的图象关于直线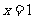 对称。
对称。
解法二(图象变换法):由函数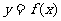 的图象向右平移1个单位得到函数
的图象向右平移1个单位得到函数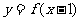 的图象;由函数
的图象;由函数
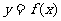 的图象关于
的图象关于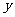 轴对称得到函数
轴对称得到函数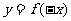 的图象,再向右平移1个单位,得到
的图象,再向右平移1个单位,得到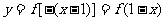 的图象。如图所示,选D。
的图象。如图所示,选D。
解法三(特值代入法):由已知可得点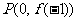 在函数
在函数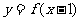 的图象上,点
的图象上,点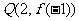 在函数
在函数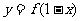 的图象上,又点P、Q关于直线
的图象上,又点P、Q关于直线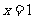 对称,选D。
对称,选D。
总结:了解一些简单结论对解题也是很有好处的。如:函数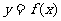 满足
满足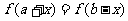 ,则函数
,则函数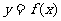 的自对称轴为
的自对称轴为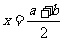 ;函数
;函数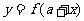 与
与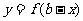 的互对称轴为
的互对称轴为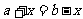 ,即
,即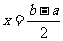
2、 值域:解决抽象函数的值域问题--定义域、对应法则决定。
材料二:若函数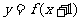 的值域为
的值域为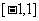 ,求函数
,求函数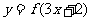 的值域。
的值域。
解析:函数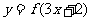 中定义域与对应法则与函数
中定义域与对应法则与函数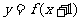 的定义域与对应法则完全相同,故函数
的定义域与对应法则完全相同,故函数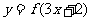 的值域也为
的值域也为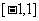 。
。
总结:当函数的定义域与对应法则不变时,函数的值域也不会改变。
1、 定义域:解决抽象函数的定义域问题--明确定义、等价转换。
材料一:若函数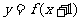 的定义域为
的定义域为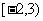 ,求函数
,求函数 的定义域。
的定义域。
解析:由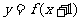 的定义域为
的定义域为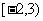 ,知
,知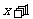 中的
中的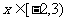 ,从而
,从而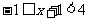 ,对函数
,对函数 而言,有
而言,有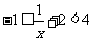 ,解之得:
,解之得: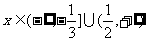 。
。
所以函数 的定义域为
的定义域为 [来源:学+科+网]
[来源:学+科+网]
总结:函数的定义域是指自变量的取值范围,求抽象函数的定义域的关键是括号内式子的地位等同(即同一对应法则后括号内 的式子具有相同的取值范围),如本题中的
的式子具有相同的取值范围),如本题中的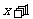 与
与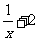 的范围等同。
的范围等同。
26.[6,13]
25.(1)易得 f(x)的定义域为{x
f(x)的定义域为{x |x∈R}.设y=
|x∈R}.设y=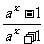 ,解得ax=-
,解得ax=-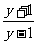 ①
①
∵ax>0当且仅当-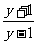 >0时,方程①有解.解-
>0时,方程①有解.解-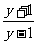 >0得-1<y<1.
>0得-1<y<1.
∴f(x)的值域为{y|-1<y<1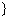 .
.
(2)f(x)=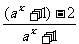 =1-
=1-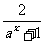 .
.
1°当a>1时,∵ax+1为增函数 ,且ax+1>0.
,且ax+1>0.
∴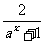 为减函数,从而f(x)=1-
为减函数,从而f(x)=1-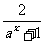 =
= 为增函数.
为增函数.
2°当0<a<1时,类似地可得f(x)= 为减函数.
为减函数.
24. (1) (-1,1)(2)略
23. (1)(-1,1), (2)(0,1)
22.解:∵(2,1)在函数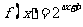 的图象上,∴1=22a+b
的图象上,∴1=22a+b
又∵(1,2)在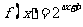 的图象上,∴2=2a+b
的图象上,∴2=2a+b
可得a=-1,b=2, ∴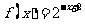
20.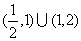 21. 4,7 ; 2,
21. 4,7 ; 2,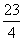
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com