
6.下列各组离子,在指定的条件下能大量共存的是
A.滴加甲基橙试剂呈红色的溶液:Fe2+、NH4+、Cl- 、NO3-
B.PH=11的溶液:S2-、SO32-、 S2O32-、Na+
C.水电离出来的c (OH-)=10-13 mol·L-1的溶液:K+、HCO3-、Br-、Ba2+
D.无色透明的溶液:K+、SiO32-、NO3-、Al3+
5.在淀粉碘化钾溶液中加入少量次氯酸钠溶液,并加入少量的稀硫酸,溶液立即变蓝,在上述溶液中加入足量的亚硫酸钠溶液,蓝色逐渐消失。下列判断不正确的是
A.氧化性:ClO –>I2>SO42–
B.在空气中漂白粉溶液可使淀粉碘化钾试纸变蓝
C.向氯水中加入亚硫酸钠溶液,氯水褪色
D.次氯酸钠可以与亚硫酸钠共存
4.若某池(电解池或原电池)的总反应离子方程式是: Cu+2H+ = Cu2+ +H2↑,关于此池的有关说法正确的是:
A.该池只能是电解池,且金属铜为该电解池的阳极
B.该池只能是原电池,且电解质溶液为硝酸
C.该池可能是原电池,也可能是电解池
D.该池只能是电解池,电解质溶液可以是硫酸铜
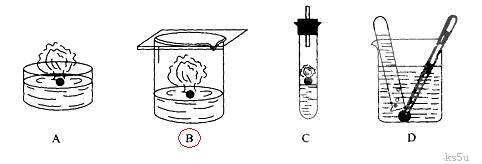
3.从实验的安全考虑,在下列四种演示金属钾与水反应的实验装置或操作较为科学
的是
2.最近日本科学家确认世界上还存在另一种“分子足球”N60,它与C60的结构相似。
下列说法正确的是
A.N60是一种新型化合物 B.N60和14N都是氮的同位素
C.N60和N2是同素异形体 D.N60和N2是同系物
1.下列分散系中,分散质粒子直径最大的是
A.雾 B.石灰乳 C.氢氧化铁胶体 D.淀粉溶液
7.(本小题满分12分)
已知数列
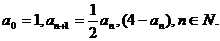
(1)证明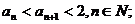
(2)求数列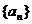 的通项公式an.
的通项公式an.
解:(1)方法一 用数学归纳法证明:
1°当n=1时,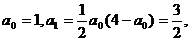
∴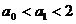 ,命题正确.
,命题正确.
2°假设n=k时有
则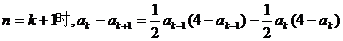
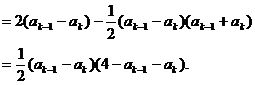
而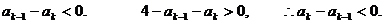
又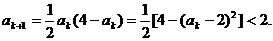
∴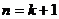 时命题正确.
时命题正确.
由1°、2°知,对一切n∈N时有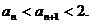
方法二:用数学归纳法证明:
1°当n=1时,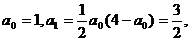 ∴
∴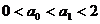 ;
;
2°假设n=k时有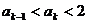 成立,
成立,
令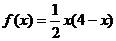 ,
,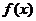 在[0,2]上单调递增,所以由假设
在[0,2]上单调递增,所以由假设
有: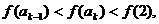 即
即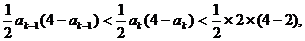
也即当n=k+1时 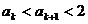 成立,所以对一切
成立,所以对一切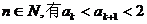
(2)下面来求数列的通项: 所以
所以
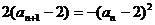
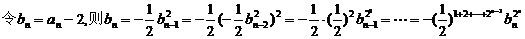 ,
,
又bn=-1,所以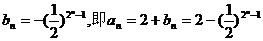
6.(本小题满分12分)
数列{an}满足 .
.
(Ⅰ)用数学归纳法证明: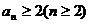 ;
;
(Ⅱ)已知不等式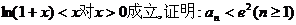 ,其中无理数e=2.71828….
,其中无理数e=2.71828….
(Ⅰ)证明:(1)当n=2时,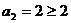 ,不等式成立.
,不等式成立.
(2)假设当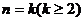 时不等式成立,即
时不等式成立,即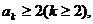
那么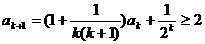 . 这就是说,当
. 这就是说,当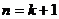 时不等式成立.
时不等式成立.
根据(1)、(2)可知: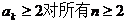 成立.
成立.
(Ⅱ)证法一:
由递推公式及(Ⅰ)的结论有 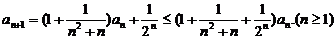
两边取对数并利用已知不等式得 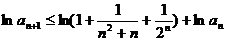
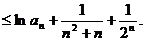 故
故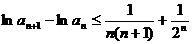
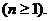
上式从1到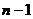 求和可得
求和可得
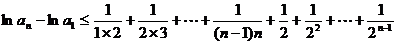
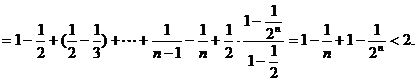
即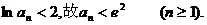
(Ⅱ)证法二:
由数学归纳法易证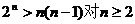 成立,故
成立,故
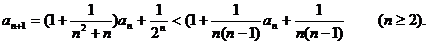
令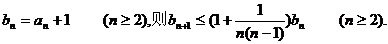
取对数并利用已知不等式得 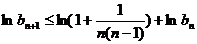
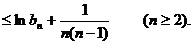
上式从2到n求和得 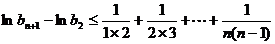
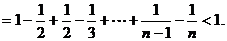
因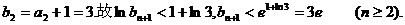
故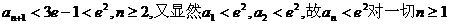 成立.
成立.
5.(本小题满分12分)
已知椭圆C1的方程为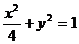 ,双曲线C2的左、右焦点分别为C1的左、右顶点,而C2的左、右顶点分别是C1的左、右焦点.
,双曲线C2的左、右焦点分别为C1的左、右顶点,而C2的左、右顶点分别是C1的左、右焦点.
(Ⅰ)求双曲线C2的方程;
(Ⅱ)若直线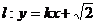 与椭圆C1及双曲线C2都恒有两个不同的交点,且l与C2的两个交点A和B满足
与椭圆C1及双曲线C2都恒有两个不同的交点,且l与C2的两个交点A和B满足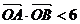 (其中O为原点),求k的取值范围.
(其中O为原点),求k的取值范围.
解:(Ⅰ)设双曲线C2的方程为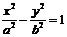 ,则
,则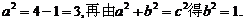
故C2的方程为
(II)将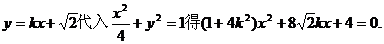
由直线l与椭圆C1恒有两个不同的交点得
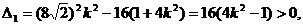
即 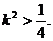 ①
①
 .
.
由直线l与双曲线C2恒有两个不同的交点A,B得
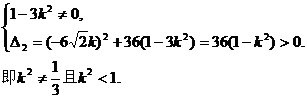

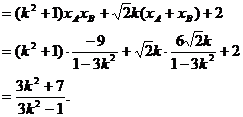
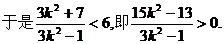 解此不等式得
解此不等式得
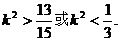 ③
③
由①、②、③得
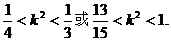
故k的取值范围为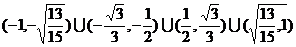
4.(本小题满分14分)
已知动圆过定点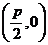 ,且与直线
,且与直线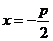 相切,其中
相切,其中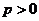 .
.
(I)求动圆圆心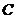 的轨迹的方程;
的轨迹的方程;
(II)设A、B是轨迹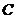 上异于原点
上异于原点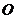 的两个不同点,直线
的两个不同点,直线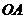 和
和 的倾斜角分别为
的倾斜角分别为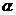 和
和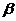 ,当
,当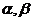 变化且
变化且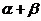 为定值
为定值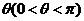 时,证明直线
时,证明直线 恒过定点,并求出该定点的坐标.
恒过定点,并求出该定点的坐标.
解:(I)如图,设 为动圆圆心,
为动圆圆心,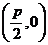 为记为
为记为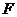 ,过点
,过点 作直线
作直线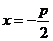 的垂线,垂足为
的垂线,垂足为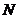 ,由题意知:
,由题意知: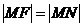 即动点
即动点 到定点
到定点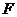 与定直线
与定直线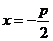 的距离相等,由抛物线的定义知,点
的距离相等,由抛物线的定义知,点 的轨迹为抛物线,其中
的轨迹为抛物线,其中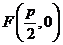 为焦点,
为焦点,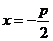 为准线,所以轨迹方程为
为准线,所以轨迹方程为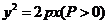 ;
;
(II)如图,设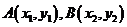 ,由题意得
,由题意得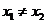 (否则
(否则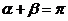 )且
)且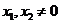 所以直线
所以直线 的斜率存在,设其方程为
的斜率存在,设其方程为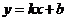 ,显然
,显然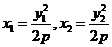 ,将
,将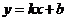 与
与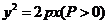 联立消去
联立消去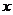 ,得
,得 由韦达定理知
由韦达定理知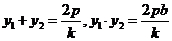 ①
①
(1)当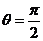 时,即
时,即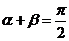 时,
时, 所以
所以 ,
, 所以
所以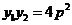 由①知:
由①知: 所以
所以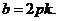 因此直线
因此直线 的方程可表示为
的方程可表示为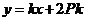 ,即
,即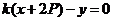 所以直线
所以直线 恒过定点
恒过定点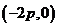
(2)当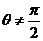 时,由
时,由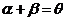 ,得
,得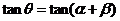 =
=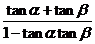 =
=
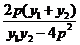 将①式代入上式整理化简可得:
将①式代入上式整理化简可得: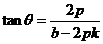 ,所以
,所以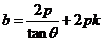 ,
,
此时,直线 的方程可表示为
的方程可表示为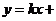
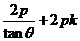 即
即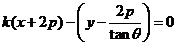
所以直线 恒过定点
恒过定点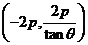
所以由(1)(2)知,当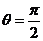 时,直线
时,直线 恒过定点
恒过定点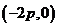 ,当
,当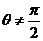 时直线
时直线 恒过定点
恒过定点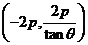 .
.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com