
2.某初级中学有学生270人,其中一年级108人,二、三年级各81人,现要利用抽样方法抽取10人参加某项调查,考虑选用简单随机抽样、分层抽样和系统抽样三种方案,使用简单随机抽样和分层抽样时,将学生按一、二、三年级依次统一编号为1,2,…,270;使用系统抽样时,将学生统一随机编号1,2,…,270,并将整个编号依次分为10段。如果抽得号码有下列四种情况:
①7,34,61,88,115,142,169,196,223,250;
②5,9,100,107,111,121,180,195,200,265;
③11,38,65,92,119,146,173,200,227,254;
④30,57,84,111,138,165,192,219,246,270;
关于上述样本的下列结论中,正确的是 
A.②、③都不能为系统抽样 B.②、④都不能为分层抽样
C.①、④都可能为系统抽样 D.①、③都可能为分层抽样
1.先后抛掷两枚均匀的正方体骰子(它们的六个面分别标有点数1、2、3、4、5、6),骰子朝上的面的点数分别为X、Y,则 的概率为
的概率为

A.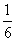 B.
B.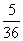 C.
C. D.
D.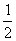

16. 直线 :
: 与双曲线C:
与双曲线C: 相交于点P、Q
相交于点P、Q
(1)当实数 为何值时,|PQ|=
为何值时,|PQ|=
(2)是否存在实数 ,使得以PQ为直径的圆经过坐标原点?若存在,求出
,使得以PQ为直径的圆经过坐标原点?若存在,求出 的值;若不存在,说明理由。
的值;若不存在,说明理由。
15. 抛物线的顶点在原点,它的准线过双曲线 的一个焦点,并于双曲线的实轴垂直,已知抛物线与双曲线的交点为
的一个焦点,并于双曲线的实轴垂直,已知抛物线与双曲线的交点为 ,求抛物线的方程和双曲线的方程。
,求抛物线的方程和双曲线的方程。
14.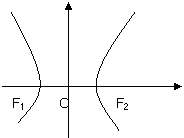 F1,F2为双曲线
F1,F2为双曲线 的焦点,过
的焦点,过 作
作
垂直于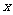 轴的直线交双曲线与点P且∠P F1F2=300,
轴的直线交双曲线与点P且∠P F1F2=300,
求双曲线的渐近线方程。
13. 椭圆短轴的一个端点与两个焦点组成一个正三角形,焦点到椭圆长轴端点的最短距离为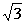 ,求此椭圆的标准方程。
,求此椭圆的标准方程。
12.直线 被抛物线
被抛物线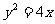 截得线段的中点坐标是
.
截得线段的中点坐标是
.
11.以原点为顶点,坐标轴为对称轴,并且经过点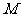 (-2,-4)的抛物线方程是
.
(-2,-4)的抛物线方程是
.
10.已知双曲线 的离心率
的离心率 ,则实数
,则实数 =
.
=
.
9.椭圆的焦点在y轴上,焦距为 ,椭圆上的点到两焦点的距离之和为8,则椭圆的标准方程为
.
,椭圆上的点到两焦点的距离之和为8,则椭圆的标准方程为
.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com