20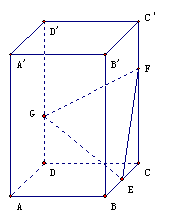．如图，正四棱柱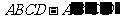中，底面边长为2，侧棱长为3，E为BC的中点，FG分别为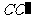、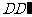上的点，且CF=2GD=2.求：

(1)到面EFG的距离；

(2)DA与面EFG所成的角；

(3)在直线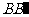上是否存在点P，使得DP//面EFG?,若

存在，找出点P的位置，若不存在，试说明理由。

18．如图，在四棱锥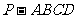中，底面ABCD是正方形，侧棱底面ABCD，

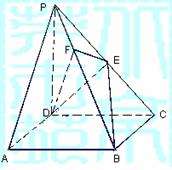
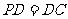　 　 ，E是PC的中点，作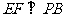交PB于点F.

　 (1)证明 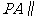平面；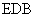

　 (2)证明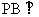平面EFD；

　 (3)求二面角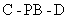的大小．

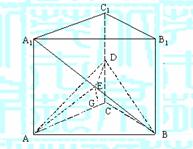　 19．(14分)如图，直三棱柱ABC-A₁B₁C₁中，底面是等腰直角三角形，∠ACB=90°，侧棱AA₁=2，D、E分别是CC₁与A₁B的中点，点E在平面ABD上的射影是△ABD的垂心G.

　 (1)求A₁B与平面ABD所成角的大小

(结果用反三角函数值表示)；

　 (2)求点A₁到平面AED的距离.

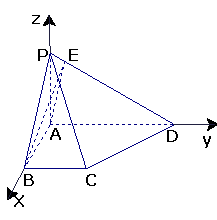
17.正三棱柱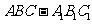的所有棱长均为2，P是侧棱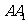上任意一点．

(Ⅰ)求证： 直线不可能与平面垂直；

(II)当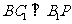时，求二面角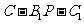的大小．　

16.　　　　　　　　 在四棱锥P－ABCD中，底面ABCD是一直角梯形，∠BAD＝90°，AD∥BC，AB＝BC＝a，AD＝2a，且PA⊥底面ABCD，PD与底面成30°(PD和其在底面上的射影所成的角)。

⑴若AE⊥PD，垂足为E，求证：BE⊥PD；

⑵求异面直线AE与CD所成角的大小。

15.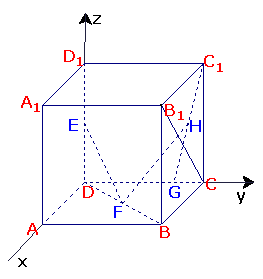在棱长为1的正方体中ABCD－A₁B₁C₁D₁中，E、F分别为DD₁、BD的中点，G在CD上，且CG＝CD/4，H为C₁G的中点，

⑴求证：EF⊥B₁C；

⑵求EF与C₁G所成角的余弦值；

⑶求FH的长。

14. 若A(3cosα, 3sinα, 1)，B(2cosθ, 2sinθ, 1)，则|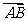|的取值范围是　　　　 。

13．空间四边形OABC中，M，N分别是边OA，BC的中点，点G在MN上，且MG = 2GN，用基底{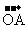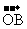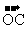，，}表示向量.　　　

12.已知S是△ABC所在平面外一点，D是SC的中点，

若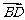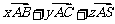＝，则x+y+z＝　　　　　　 ．

11．已知向量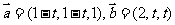，则的最小值为　　　　

10．同时垂直向量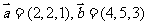的单位向量是