3.下列命题正确的序号是______.

　⑴无限集的真子集是有限集　　　　　　　　 ⑵任何一个集合必定有两个子集

⑶自然数集是整数集的真子集　　　　　　 　⑷{1}是质数集的真子集

解：必须对概念把握准确，并不是所有有限集都是无限集子集，如{1}不是{x｜x＝2k，k∈Z}的子集，排除⑴⑴.由于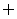只有一个子集，即它本身，排除⑵.由于1不是质数，排除⑷.故选⑶.

3.集合A＝{x｜－1＜x＜3，x∈Z}，写出A的真子集___________________________.

分析：区分子集与真子集的概念.空集是任一非空集合的真子集，一个含有n个元素的子集有2ⁿ，真子集有2ⁿ－1个.

则该题先找该集合元素，后找真子集.

解：因－1＜x＜3，x∈Z，故x＝0，1，2

即a＝{x｜－1＜x＜3，x∈Z}＝{0，1，2}

真子集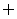：、{1}、{2}、{0}、{0，1}、{0，2}、{1，2}，共7个

2.判断下列说法是否正确，并在题后括号内填“√”或“×”.

(1)若S＝{1，2，3}，A＝{2，1}，则C_SA＝{2，3}　　　　　 　　　　　　　　(　　 )

(2)若S＝{三角形}，A＝{直角三角形}，则C_SA＝{锐角或钝角三角形}　　　　 (　　 )

(3)若U＝{四边形}，A＝{梯形}，则C_UA＝{平行四边形}　　　　　　　　　　 (　　 )

(4)若U＝{1，2，3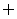}，A＝，则C_UA＝A　　　　　　　　　　　　　　　　　 (　　 )

(5)若U＝{1，2，3}，A＝5，则C_UA＝　　　　　　　　　 　　　　　　　　(　　 )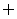

(6)若U＝{1，2，3}，A＝{2，3}，则C_UA＝{1}　　　 　　　　　　　　　　　(　　 )

(7)若U是全集且AB，则C_UAC_UB　　　　　　　　　　　　　　　　　　 (　　 )

解：紧扣定义，利用性质求解相关题目.(2)(5)(6)正确，其余错误.

在(1)中，因S＝{1，2，3}，A＝{2，1}，则C_SA＝{3}.

(2)若S＝{三角形}，则由A＝{直角三角形}得C_SA＝{锐角或钝角三角形}.

(3)由梯形及平行四边形构成的图形集合不一定是四边形的全部.如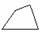既不是梯形，也不是平行四边形.

(4)因U＝{1，2，3}，A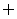＝，故C_UA＝U.

(5)U＝{1，2，3}，A＝5，则C_UA＝.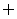

(6)U＝{1，2，3}，A＝{2，3}，则C_UA＝{1}.

(7)若U是全集且A＝B，则C_UA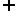C_UB.

评述：上述题目涉及补集较多，而补集问题解决前提必须考虑全集，故一是先看全集U，二是由A找其补集，应有A∪(C_UA)＝U.

1.判断正误，并在题后括号内填“√”或“×”.

(1)空集没有子集　　　　　　　　　　　　　　　　　　　　　　 　　　　　(　　 )

(2)空集是任何一个集合的真子集　　　　　　　　　　　　　　　 　　　　　(　　 )

(3)任一集合必有两个或两个以上子集　　　　　　　　　　　　　 　　　　　(　　 )

(4)若B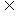A，那么凡不属于集合a的元素，则必不属于B　　　　 　　　　　(　　 )

分析：关于判断题应确实把握好概念的实质.

解：该题的5个命题，只有(4)是正确的，其余全错.

对于(1)、(2)来讲，由规定：空集是任何一个集合的子集，且是任一非空集合的真子集.

对于(3)来讲，可举反例，空集这一个集合就只有自身一个子集.

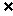对于(4)来讲，当x∈B时必有x∈A，则xA时也必有xB.

2.预习提纲：

(1)交集与并集的含义是什么?能否说明?

(2)求两个集合交集或并集时如何借助图形.

1.完成课时训练二

3.充分利用“形”来解决问题.

2.补集的概念必须要有全集的限制.

1.两个集合之间的基本关系只有“包含”与“相等”两种，可类比两个实数间的大小关系，同时还要注意区别“属于”与“包含”两种关系及其表示方法.

例1写出集合{a，b}的所有的子集.

解析：Ø,{a},{b},{a,b}

变：写出集合{a，b，c}的所有的子集.

解析：Ø,{a},{b},{c},{a,b},{a,c},{b,c},{a,b,c}

猜想：若A中有n个元素，A的子集有______个.

解析：2ⁿ

例2下列三个集合中，哪两个集合具有包含关系？

⑴S＝{―2,―1,1,2}，A＝{―1,1}，B＝{―2,2}；

⑵S＝R，A＝{x|x≤0,x∈R}，B＝{x|x＞0,x∈R}；

⑶S＝{x|x为地球人}，A＝{x|x为中国人}，B＝{x|x为外国人}.

解析：⑴⑵⑶中都有AS，BS.

用图表示为

思考：观察例2中每一组的三个集合，它们之间还有一种什么关系？

例3　不等式组的解集为A，U＝R，试求A及C_UA.

解析：A＝{x|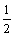＜x≤2}

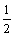　　C_UA＝{x|x≤或x＞2}

点评：不等式问题通常借助数轴来研究，但要注意实心点与空心点.

学生练习：

A组P9练习3,4(老师巡视，个别释疑)

B组P10习题1,2,3,4,5