
4.掌握正确的复习方法,提高效率
数学总复习一般要经历三个阶段,第一阶段是把课本上的所有高考内容系统复习一遍;第二阶段可搞些专题复习;第三阶段进行综合训练(适应性训练)。在临考前做到三个回归,即回归教材,回归基础,回归近几年的高考题。在复习备考的整个过程中,始终要关注以下五个问题:⑴立足基础,教会学生学习;⑵依纲据本,注重新增内容的复习;⑶着眼能力,抓好应用题、开放题(探索题)的训练,增强学生的实践意识和创新意识;⑷交出“权力”,多给学生留出时间,倡导自主学习,营造自主探索和合作交流的环境;⑸精选习题,强化审题和分析,联系地运动地观察、分析、思考问题,提高学生解决问题的能力;⑹重视多次“反馈”,及时弥补学习上的缺漏;⑺分类指导,加强后期复习的针对性。
3.强化“四基”的教学与训练,夯实基础
所谓“四基”就是指基础知识、基本技能、基本数学思想方法和基本数学活动经验,从今年高考数学试题可见“出活题、考基础、考能力”仍是命题的主导思想。因而在复习时应加强“四基”的教学与训练,不要急于求成,好高骛远,抓了高深的,丢了基本的。复习基础知识一是简单的重复,即把知识按原来的顺序简明扼要地重新反思一遍;二是再设计的重复,即抓住本学科内各部分内容之间的联系与综合进行重新组合,使学生对所学知识的认识形成一个较为完整的结构,达到“牵一发而动全身”的境界。强化基本技能的训练,克服“眼高手低”现象,主要在速算、语言表达、解题、反思矫正等方面下功夫,尽量不丢或少丢一些不应该丢失的分数。注重基本数学思想方法在日常训练中的渗透,逐步融入到学生的“血脉”之中,才能提高学生的思维能力。注意与初高中数学新课程接轨,设计一些考查学生动手操作的试题,让学生积累解决问题的一些外显的操作活动经验和内隐的思维活动经验,从活动过程中亲身体验寻找解决问题的方法,提高分析问题和解决问题的能力。从今年高考试卷中学生发生的错误来看,也主要是“四基”的训练未落到实处。
1.学习《数学科考试大纲》,明确要求
通过学习《考试说明》,明确考试的性质、内容、形式与基本结构。研究每一年《考试大纲》的变化及对高考试题的影响。特别是重庆将发布的有关《考试说明》是我们复习备考的重要依据,要逐条落实考试内容,有针对性的培养综合考试所要求的五种能力,即思维能力、运算能力、空间想象能力以及实践能力和创新意识。同时要明确今年高考在内容、难度和题型要求上将要发生的变化,哪些内容被删去了,哪些内容降低了要求,哪些内容是增加的,都要做到心中有数。另外注意教育部颁布的普通高中《数学课程标准》,将引领数学教学改革与高考改革的方向。
下面统计数据均不包括零分和缺考人数。通过近三年统计数据的各项指标来看,文理科数学试题有逐年难度加大的趋势,要实现重庆卷在难度上保持相对稳定的目标,还有待命题者们继续努力。从统计表中还看到今年文、理科试卷整体的信度较高,标准差适中,区分度较好,但个别题目需调整完善。如文科的第8、9、10、14、15题和理科的第9、10题区分度明显偏低。
表一:文科选择题统计数据表
表二:理科选择题统计数据表
表三:文科填空题统计数据表
表四:理科填空题统计数据表
表五:文科解答题统计数据表
表六:理科解答题统计数据表
表七:文理科数学成绩分段人数统计表
|
|
文科(64480人) |
理科(106046人) |
||
|
1――10分 |
1080 |
1.67% |
388 |
0.37% |
|
11――20分 |
3293 |
5.10% |
1398 |
1.32% |
|
21--30分 |
4799 |
7.43% |
2272 |
2.14% |
|
31--40分 |
5346 |
8.28% |
3082 |
2.91% |
|
41--50分 |
5573 |
8.63% |
4562 |
4.30% |
|
51--60分 |
5442 |
8.43% |
6803 |
6.41% |
|
61--70分 |
5084 |
7.88% |
10003 |
9.43% |
|
71--80分 |
5584 |
8.65% |
13462 |
12.69% |
|
81--90分 |
6537 |
10.13% |
16270 |
15.34% |
|
91--100分 |
7528 |
11.66% |
16647 |
15.69% |
|
101--110分 |
7256 |
11.24% |
14317 |
13.50% |
|
111--120分 |
4850 |
7.51% |
10044 |
9.47% |
|
121--130分 |
1794 |
2.78% |
5146 |
4.85% |
|
131――140分 |
360 |
0.56% |
1562 |
1.47% |
|
141――150分 |
28 |
0.04% |
118 |
0.11% |
表八:文理科数学全卷成绩统计数据表
|
项目 |
平均分 |
标准差 |
信度 |
难度 |
及格率 |
优生率 |
最高分 |
有效分 |
||||
|
专一 |
三本 |
二本 |
重点 |
|||||||||
|
文 科 |
2007年 |
76.17 |
|
|
0.508 |
40% |
|
149 |
84 |
92 |
104 |
121 |
|
2008年 |
74.00 |
36.05 |
0.912 |
0.493 |
37.13% |
12.31% |
147 |
83 |
90 |
105 |
124 |
|
|
2009年 |
70.57 |
32.12 |
0.913 |
0.471 |
34.44% |
3.64% |
147 |
80 |
87 |
97.5 |
112 |
|
|
理 科 |
2007年 |
90.83 |
|
|
0.606 |
60% |
|
150 |
94 |
100 |
106 |
117 |
|
2008年 |
87.50 |
30.69 |
0.904 |
0.583 |
53.58% |
12.96% |
150 |
91 |
97 |
103 |
114 |
|
|
2009年 |
84.40 |
26.01 |
0.870 |
0.563 |
45.92% |
6.83% |
150 |
84 |
89 |
95 |
106.5 |
4.文理科填空题、立几解答题难度偏大,压轴题的难度可适当再降低。文科填空题没有一个题的难度值在0.7以上,后面三个填空题难度值在0.5以下,难度值最低为0.01,难得不可想象;理科填空题后面三个的难度值都在0.5以下,难度值最低为0.08,也不令人满意。文科立几第18题难度值为0.25,其难度与压轴题的难度相当,这也是文科学生的空间想象能力较差所致;理科立几第19题难度值为0.44,也不容乐观。文科第20、21题的难度值分别为0.24、0.18;理科第20、21题的难度值分别为0.30、0.07,这些说明文理科最后两个解答题的难度值都在0.3及以下,特别是理科最后一题属超难题,有形同虚设之感。实际上,今年文理科第20题的难度已经是最后压轴题的难度了,建议今后文理科最后一道压轴题的难度能够保持在0.2左右就较为理想了。
3.少数题目结构不尽合理,有画蛇添足、人为制造难度之嫌。如文科第20题的第2小题本来求 的最小值就行了,但还要求学生求此时
的最小值就行了,但还要求学生求此时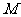 点的坐标就显得多余了,并且求解
点的坐标就显得多余了,并且求解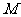 点的坐标并非易事,要解二元二次方程组
点的坐标并非易事,要解二元二次方程组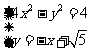 运算量较大,其结果也不简捷,况且初中数学新课程对二元二次方程组也不作要求了。又如理科第20题的第1小题要先求出已知椭圆的方程,才能求
运算量较大,其结果也不简捷,况且初中数学新课程对二元二次方程组也不作要求了。又如理科第20题的第1小题要先求出已知椭圆的方程,才能求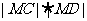 的最大值,而
的最大值,而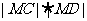 的最大值与本题第2小题毫无关系,但椭圆的方程对第2小题有直接影响,因此,本题不如把第1小题改为求椭圆的方程,这样设计就显得题目结构和谐完美。
的最大值与本题第2小题毫无关系,但椭圆的方程对第2小题有直接影响,因此,本题不如把第1小题改为求椭圆的方程,这样设计就显得题目结构和谐完美。
2.个别知识点考查过多,有重复考查之嫌。本次考试对组合内容、平面向量的数量积考查较多,两次出现“至少”一词。如理科第6、13、17题都对组合内容进行了考查,且理科第6、13题都出现了“至少”一词,理科涉及平面向量的数量积有第4、7、20(2)题。由此建议尽量在同一试卷中避免同一知识点的多次考查。
1.起点题的难度偏高,全卷运算量较大。这次送分的基础题是常规常见题,但考查的知识点较多,且每道题都有一定量的运算,致使相当一部分学生在前面花费了不少时间,后面能够解决的一些问题因时间不够而望题兴叹。如文科第1题(选择题第一题)平均3.94分,比后面的第2、3、4题的平均分都低,文科第11题(填空题第一题)平均3.07分,比后面的第12题的平均分低,文科第16题(解答题第一题)平均6.84分,比后面的第17题的平均分低,理科的第2题(选择题第二题)平均4.47分,比后面的第3、4题的平均分低,理科的第16题(解答题第一题)平均7.98分,比后面的第17题的平均分低,这些充分说明,起点题的分数要送就送到手,不要害怕题简单,毕竟存在大量中下学生参加高考。另外,这次考题对学生的运算水平进行了一次大检验,算得有点叫人难受,有用运算量来增加难度的感觉。如文科除第2、11题外,理科除第1、9题外,其余每道题都有一定量的运算,有些题的运算量真是不算不知道,一算吓一跳。如文科第8、9、15题和20题的求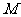 点的坐标等,理科第6、10、15、20(2)题等。希望今后能够控制每个题的运算量,增大思考的力度,不在运算上兜圈子,多设置一些“一眼望穿”的有一定思维含量的题目。
点的坐标等,理科第6、10、15、20(2)题等。希望今后能够控制每个题的运算量,增大思考的力度,不在运算上兜圈子,多设置一些“一眼望穿”的有一定思维含量的题目。
6.注意纵向横向联系,体现初高中、新旧课程内容的衔接
今年高考试题紧密结合初高中课改进程,汲取了新课程中的新思想、新理念,并注意从内容上相衔接。第一,注重对新增内容的考查,特别是对新课改要求比较高的内容的考查。如文理科第4题和理科第7、20(2)题是对平面向量的有关内容进行考查;文科第14题和理科第17(2)题是对统计内容进行考查;文科第8、17题和理科第6、17(1)题是对概率的内容进行考查;文科第10、19题和理科第8、18题是对导数及其应用与函数极限的相关知识的考查,更为重要的是考纲中“理解可导函数的单调性与其导数的关系”得到了重点体现。新增内容文科分值约占40分左右,理科分值约占53分左右,比例远远高于在平常教学课时中所占比例,其中统计与概率、导数、极限这些内容在当今小学、初高中的新课改中是要求相当高的。第二,注意初高中新课程对图象变换、函数与方程等内容的要求。初中旧教材对图形变换要求较低,现在初中数学新课程对图形的平移、对折(对称)、旋转、相似等变换作了高要求,不仅从几何的角度去研究,还从坐标的角度去研究这些变换,为我们高中数学学习打下了坚实的基础;高中数学新课程对函数与方程的内容比过去要求更高,要求学生了解函数的零点与方程根的联系,能够借助计算器用二分法求相应方程的近似解等。上述这些内容在这次考题中都有所体现,如文理科第10题不仅体现了对图象变换的考查,而且体现了对函数的零点与方程根的联系的考查,对图象变换内容考查的还有:文科第16(2)、20(2)题,理科第9、16(2)、20(2)题,突出了对运动变换思想的考查,加大了“变”与“不变”的转换,提高了空间思维的含量,不避免地增加了解决这些问题的难度。第三,注意与初中数学新课程的内容相衔接,尽量在高考题中不出现初中未学过内容的运用。如立方和(差)公式、高次方程(组)的求解、分组分解法等等。
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com