
例4. 侦察卫星在通过地球两极上空的圆轨道上运行,它的运行轨道距地面高为h,要使卫星在一天的时间内将地面上赤道各处在日照条件下的情况全部都拍摄下来,卫星在通过赤道上空时,卫星上的摄影像机至少应拍地面上赤道圆周的弧长是多少?设地球半径为R,地面处的重力加速度为g,地球自转的周期为T。
解析:设卫星周期为T1,那么:
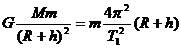 ①
①
又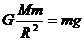 ②
②
有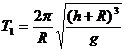 ③
③
地球自转角速度为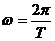 ④
④
在卫星绕行地球一周的时间T1内,地球转过的圆心角为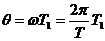 ⑤
⑤
那么摄像机转到赤道正上方时摄下圆周的弧长为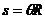 ⑥
⑥
由①②③④⑤⑥得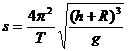
例3. (2004年北京高考)如图5是某种静电分选器的原理示意图。两个竖直放置的平行金属板带有等量异号电荷,形成匀强电场,分选器漏斗的出口与两板上端处于同一高度,到两板距离相等。混合在一起的a、b两种颗粒从漏斗出口下落时,a种颗粒带上正电,b种颗粒带上负电。经分选电场后,a、b两种颗粒分别落到水平传送带A、B上。
已知两板间距d=0.1m,板的度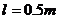 ,电场仅局限在平行板之间;各颗粒所带电量大小与其质量之比均为
,电场仅局限在平行板之间;各颗粒所带电量大小与其质量之比均为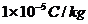 。设颗粒进入电场时的初速度为零,分选过程中颗粒大小及颗粒间的相互作用力不计。要求两种颗粒离开电场区域时,不接触到极板但有最大偏转量。重力加速度g取
。设颗粒进入电场时的初速度为零,分选过程中颗粒大小及颗粒间的相互作用力不计。要求两种颗粒离开电场区域时,不接触到极板但有最大偏转量。重力加速度g取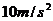 。
。
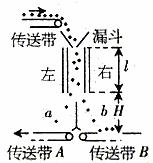
图5
(1)左右两板各带何种电荷?两极板间的电压多大?
(2)若两带电平行板的下端距传送带A、B的高度H=0.3m,颗粒落至传送带时的速度大小是多少?
(3)设颗粒每次与传送带碰撞反弹时,沿竖直方向的速度大小为碰撞前竖直方向速度大小的一半。写出颗粒第n次碰撞反弹高度的表达式。并求出经过多少次碰撞,颗粒反弹的高度小于0.01m。
解析:(1)左板带负电荷,右板带正电荷。依题意,颗粒在平行板间的竖直方向上满足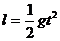
在水平方向上满足: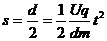
两式联立得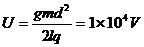
(2)根据动能定理,颗粒落到水平传送带上满足
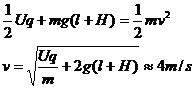
(3)在竖直方向颗粒作自由落体运动,它第一次落到水平传送带上沿竖直方向的速度
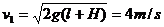
反弹高度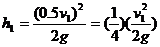
根据题设条件,颗粒第n次反弹后上升的高度:
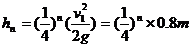
当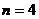 时,
时,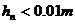
例2. (2005年上海高考)一水平放置的圆盘绕竖直固定轴转动,在圆盘上沿半径开有一条宽度为2mm的均匀狭缝。将激光器与传感器上下对准,使二者间连线与转轴平行,分别置于圆盘的上下两侧,且可以同步地沿圆盘半径方向匀速移动,激光器连续向下发射激光束。在圆盘转动过程中,当狭缝经过激光器与传感器之间时,传感器接收到一个激光信号,并将其输入计算机,经处理后画出相应图线。图4(a)为该装置示意图,图4(b)为所接收的光信号随时间变化的图线,横坐标表示时间,纵坐标表示接收到的激光信号强度,图中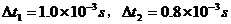 。
。
(1)利用图(b)中的数据求1s时圆盘转动的角速度;
(2)说明激光器和传感器沿半径移动的方向;
(3)求图(b)中第三个激光信号的宽度△t3。
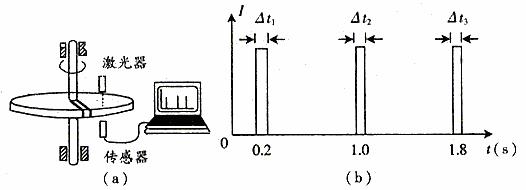
图4
解析:(1)由图线读得,转盘的转动周期 ,
,
角速度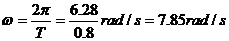
(2)激光器和探测器沿半径由中心向边缘移动(理由为:由于脉冲宽度在逐渐变窄,表明光信号能通过狭缝的时间逐渐减少,即圆盘上对应探测器所在位置的线速度逐渐增加,因此激光器和探测器沿半径由中心向边缘移动)。
(3)设狭缝宽度为d,探测器接收到第i个脉冲时距转轴的距离为ri,第i个脉冲的宽度为△ti,激光器和探测器沿半径的运动速度为v。

由以上式联立解得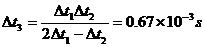
评点:将直线运动与圆周运动组合,在近年高考中出现率极高,如2000年全国高考中“激光束转动测小车的速度”等,破题的关键是抓住时间、空间的关联。
例1. (04年广东高考)一路灯距地面的高度为h,身高为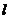 的人以速度v匀速行走,如图1所示。
的人以速度v匀速行走,如图1所示。
(1)试证明人的头顶的影子作匀速运动;
(2)求人影的长度随时间的变化率。
图1
解法1:(1)设t=0时刻,人位于路灯的正下方O处,在时刻t,人走到S处,根据题意有OS=vt,过路灯P和人头顶的直线与地面的交点M为t时刻人头顶影子的位置,如图2所示。OM为人头顶影子到O点的距离。
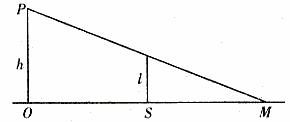
图2
由几何关系,有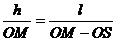
联立解得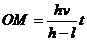
因OM与时间t成正比,故人头顶的影子作匀速运动。
(2)由图2可知,在时刻t,人影的长度为SM,由几何关系,有SM=OM-OS,由以上各式得
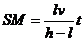
可见影长SM与时间t成正比,所以影长随时间的变化率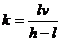 。
。
解法2:本题也可采用“微元法”。设某一时间人经过AB处,再经过一微小过程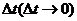 ,则人由AB到达A’B’,人影顶端C点到达C’点,由于
,则人由AB到达A’B’,人影顶端C点到达C’点,由于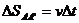 则人影顶端的移动速度:
则人影顶端的移动速度:
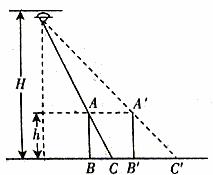
图3
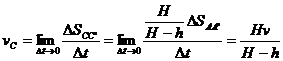
可见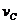 与所取时间
与所取时间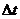 的长短无关,所以人影的顶端C点做匀速直线运动。
的长短无关,所以人影的顶端C点做匀速直线运动。
评点:本题由生活中的影子设景,以光的直进与人匀速运动整合立意。解题的核心是利用时空将两种运动组合,破题的难点是如何借助示意图将动态过程静态化,运用几何知识解答。
平抛运动:水平匀速、竖直方向自由落体
匀速圆周运动:
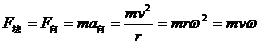
[模型讲解]
匀速直线运动:两种方法(公式法与图象法)
匀变速直线运动: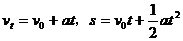 ,几个推论、比值、两个中点速度和一个v-t图象。
,几个推论、比值、两个中点速度和一个v-t图象。
特例1:自由落体运动为初速度为0的匀加速直线运动,a=g;机械能守恒。
特例2:竖直上抛运动为有一个竖直向上的初速度v0;运动过程中只受重力作用,加速度为竖直向下的重力加速度g。特点:时间对称(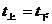 )、速率对称(
)、速率对称(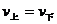 );机械能守恒。
);机械能守恒。
4. 地球同步卫星的线速度:地球同步卫星的线速度大小为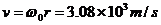 ,为定值,绕行方向与地球自转方向相同。
,为定值,绕行方向与地球自转方向相同。
[误区点拨]
天体运动问题:人造卫星的轨道半径与中心天体半径的区别;人造卫星的发射速度和运行速度;卫星的稳定运行和变轨运动;赤道上的物体与近地卫星的区别;卫星与同步卫星的区别。
人造地球卫星的发射速度是指把卫星从地球上发射出去的速度,速度越大,发射得越远,发射的最小速度,恰好是在地球表面附近的环绕速度,但人造地球卫星发射过程中要克服地球引力做功,增大势能,所以将卫星发射到离地球越远的轨道上,在地面上所需要的发射速度就越大。
混淆连续物和卫星群:连续物是指和天体连在一起的物体,其角速度和天体相同,而对卫星来讲,其线速度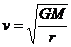 。
。
双星系统中的向心力中的距离与圆周运动中的距离的差别。
[模型演练]
(2005年大联考)经过用天文望远镜长期观测,人们在宇宙中已经发现了许多双星系统,通过对它们的研究,使我们对宇宙中物质的存在形式和分布情况有了较深刻的认识,双星系统由两个星体组成,其中每个星体的线度都远小于两星体之间的距离,一般双星系统距离其他星体很远,可以当作孤立系统来处理。
现根据对某一双星系统的光度学测量确定;该双星系统中每个星体的质量都是M,两者相距L,它们正围绕两者连线的中点做圆周运动。
(1)试计算该双星系统的运动周期 ;
;
(2)若实验中观测到的运动周期为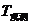 ,且
,且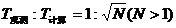 。
。
为了理解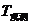 与
与 的不同,目前有一种流行的理论认为,在宇宙中可能存在一种望远镜观测不到的暗物质。作为一种简化模型,我们假定在以这两个星体连线为直径的球体内均匀分布这种暗物质。若不考虑其他暗物质的影响,请根据这一模型和上述观测结果确定该星系间这种暗物质的密度。
的不同,目前有一种流行的理论认为,在宇宙中可能存在一种望远镜观测不到的暗物质。作为一种简化模型,我们假定在以这两个星体连线为直径的球体内均匀分布这种暗物质。若不考虑其他暗物质的影响,请根据这一模型和上述观测结果确定该星系间这种暗物质的密度。
答案:(1)双星均绕它们连线的中点做圆周运动,设运动的速率为v,得:
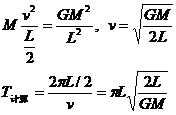
(2)根据观测结果,星体的运动周期:
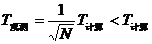
这种差异是由双星系统(类似一个球)内均匀分布的暗物质引起的,均匀分布双星系统内的暗物质对双星系统的作用,与一个质点(质点的质量等于球内暗物质的总质量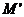 且位于中点O处)的作用相同。考虑暗物质作用后双星的速度即为观察到的速度
且位于中点O处)的作用相同。考虑暗物质作用后双星的速度即为观察到的速度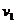 ,则有:
,则有:
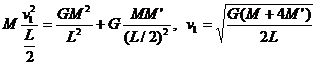
因为周长一定时,周期和速度成反比,得:
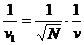
有以上各式得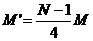
设所求暗物质的密度为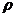 ,则有
,则有
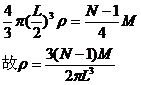
3. 地球同步卫星的轨道半径:据牛顿第二定律有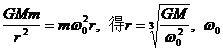 与地球自转角速度相同,所以地球同步卫星的轨道半径为
与地球自转角速度相同,所以地球同步卫星的轨道半径为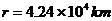 。其离地面高度也是一定的,距地面高度
。其离地面高度也是一定的,距地面高度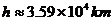 处。
处。
2. 地球同步卫星的周期:地球同步卫星的运转周期与地球自转周期相同。
1. 地球同步卫星的轨道平面:非同步人造地球卫星其轨道平面可与地轴有任意夹角,而同步卫星一定位于赤道的正上方,不可能在与赤道平行的其他平面上。
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com