
7.在实验室可利用浓盐酸与二氧化锰共热制氯气,制备装置中须安装分液漏斗而不能使用长颈漏斗,有关原因叙述错误的是 ( )
A.防止氯气通过漏斗扩散到空气中造成污染 B.便于控制加入浓盐酸的量
C.因长颈漏斗加热时容易破裂 D尽量避免HC1挥发到空气中
8关于实验室制备乙烯的实验。下列说法正确的是 ( )
A.反应物是乙醇和过量的3 mol·L-1硫酸的混合液
B.温度计插入反应溶液液面以下,以便控制温度在140℃
C.反应容器(烧瓶)中应加入少许瓷片
D.反应完毕先灭火再从水中取出导管
6.下列反应适用于实验室制备氧气的是 ( )
 ①高锰酸钾分解:2KMn04
K2Mn04+Mn02+02↑
①高锰酸钾分解:2KMn04
K2Mn04+Mn02+02↑
 ②硝酸铵分解:2NH4N03
2N2↑十02↑+4H20
②硝酸铵分解:2NH4N03
2N2↑十02↑+4H20
Mn02
③过氧化氢催化分解: 2H2O2 ==== O2↑+2H20
 ④ N02热分解:2N02 2NO+O2
④ N02热分解:2N02 2NO+O2
A.只有① B.①和② C.①和③ D.①③④
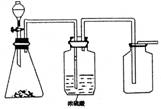
5.下图是一套实验室制气装置。用于发生、干燥和收集气体。下列各组物质中,能利用这套装置进行实验的是 (填正确选硬的标号)。
A.铜屑和浓硝酸 B.二氧化锰和浓盐酸 C.电石和水 D.碳酸钙与稀盐酸
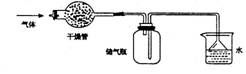
4.下图所示的装置最适宜于干燥、收集的气体是 ( )
A.NO2 B.HC1 C.CH4 D.NH3
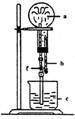
3.在上图装置中,烧瓶中充满干燥气体a,将滴管中的液体b挤入烧瓶内,轻轻振荡烧瓶,然后打开弹夹f,烧杯中的液体b呈喷泉状喷出,最终几乎充满烧瓶。则a和b分别是 ( )
|
|
a(干燥气体) |
b(液体) |
|
(A) |
NO2 |
水 |
|
(B) |
CO2 |
4mol·L-1NaOH溶液 |
|
(C) |
Cl2 |
饱和NaCl溶液 |
|
(D) |
NH3 |
1mol·L-1盐酸 |
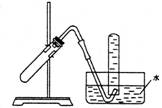
2.下图的装置可用于 ( )
A.加热小苏打制二氧化碳 B.用铜与稀硝酸反应制一氧化氮
C.用氯化铵与浓氢氧化钠溶液反应制氨气 D.用氯化钠与浓硫酸反应制氯化氢
 |
|||||
 |
|||||
|
|||||
1.按下述实验方法制备气体,合理而又实用的是 ( )
A.锌粒与稀硝酸反应制备H2
B.向饱和氯化钠溶液中滴加浓硫酸制备HC1
C.亚硫酸钠与浓硫酸反应制备SO2
D.大理石与浓硫酸反应制备CO2
例2. 如图3所示,某人通过一根跨过定滑轮的轻绳提升一个质量为m的重物,开始时人在滑轮的正下方,绳下端A点离滑轮的距离为H。人由静止拉着绳向右移动,当绳下端到B点位置时,人的速度为v,绳与水平面夹角为θ。问在这个过程中,人对重物做了多少功?
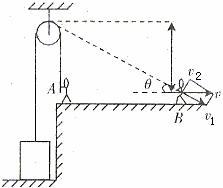
图3
解析:人移动时对绳的拉力不是恒力,重物不是做匀速运动也不是做匀变速运动,故无法用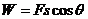 求对重物做的功,需从动能定理的角度来分析求解。
求对重物做的功,需从动能定理的角度来分析求解。
当绳下端由A点移到B点时,重物上升的高度为:
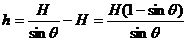
重力做功的数值为:

当绳在B点实际水平速度为v时,v可以分解为沿绳斜向下的分速度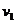 和绕定滑轮逆时针转动的分速度
和绕定滑轮逆时针转动的分速度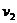 ,其中沿绳斜向下的分速度
,其中沿绳斜向下的分速度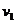 和重物上升速度的大小是一致的,从图中可看出:
和重物上升速度的大小是一致的,从图中可看出:
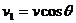
以重物为研究对象,根据动能定理得:
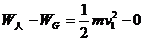
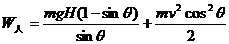
[实际应用]
小船渡河
两种情况:①船速大于水速;②船速小于水速。
两种极值:①渡河最小位移;②渡河最短时间。
例3. 一条宽度为L的河,水流速度为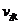 ,已知船在静水中速度为
,已知船在静水中速度为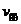 ,那么:
,那么:
(1)怎样渡河时间最短?
(2)若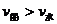 ,怎样渡河位移最小?
,怎样渡河位移最小?
(3)若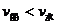 ,怎样渡河船漂下的距离最短?
,怎样渡河船漂下的距离最短?
解析:(1)小船过河问题,可以把小船的渡河运动分解为它同时参与的两个运动,一是小船运动,一是水流的运动,船的实际运动为合运动。如图4所示。设船头斜向上游与河岸成任意角θ。这时船速在垂直于河岸方向的速度分量为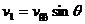 ,渡河所需要的时间为
,渡河所需要的时间为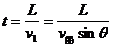 ,可以看出:L、v船一定时,t随sinθ增大而减小;当
,可以看出:L、v船一定时,t随sinθ增大而减小;当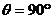 时,
时,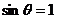 (最大)。所以,船头与河岸垂直
(最大)。所以,船头与河岸垂直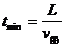 。
。
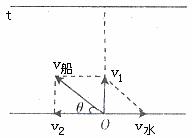
图4
(2)如图5所示,渡河的最小位移即河的宽度。为了使渡河位移等于L,必须使船的合速度v的方向与河岸垂直,即使沿河岸方向的速度分量等于0。这时船头应指向河的上游,并与河岸成一定的角度θ,所以有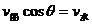 ,即
,即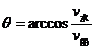 。
。

图5
因为 ,所以只有在
,所以只有在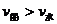 时,船才有可能垂直河岸渡河。
时,船才有可能垂直河岸渡河。
(3)若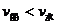 ,则不论船的航向如何,总是被水冲向下游,怎样才能使漂下的距离最短呢?
,则不论船的航向如何,总是被水冲向下游,怎样才能使漂下的距离最短呢?
如图6所示,设船头v船与河岸成θ角。合速度v与河岸成α角。可以看出:α角越大,船漂下的距离x越短,那么,在什么条件下α角最大呢?以v水的矢尖为圆心,v船为半径画圆,当v与圆相切时,α角最大,根据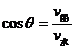
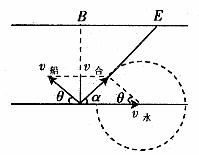
图6
船头与河岸的夹角应为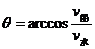 ,船沿河漂下的最短距离为:
,船沿河漂下的最短距离为:
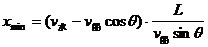
此时渡河的最短位移: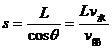
误区:不分条件,认为船位移最小一定是垂直到达对岸;将渡河时间最短与渡河位移最小对应。
[模型要点]
处理“速度关联类问题”时,必须要明白“分运动”与“合运动”的关系:
(1)独立性:一物体同时参与几个分运动时,各分运动独立进行,各自产生效果(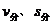 )互不干扰。
)互不干扰。
(2)同时性:合运动与分运动同时开始、同时进行、同时结束。
(3)等效性:合运动是由各分运动共同产生的总运动效果,合运动与各分运动同时发生、同时进行、同时结束,经历相等的时间,合运动与各分运动总的运动效果可以相互替代。
功是中学物理中的重要概念,它体现了力对物体的作用在空间上的累积过程,尤其是变力做功中更能体现出其空间积累的过程。所以在处理变力功可采用动能定律、功能原理、图象法、平均法等。
[模型演练]
(2005祁东联考)小河宽为d,河水中各点水流速度大小与各点到较近河岸边的距离成正比,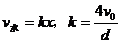 ,x是各点到近岸的距离,小船船头垂直河岸渡河,小船划水速度为
,x是各点到近岸的距离,小船船头垂直河岸渡河,小船划水速度为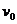 ,则下列说法中正确的是( )
,则下列说法中正确的是( )
A. 小船渡河的轨迹为曲线
B. 小船到达离河岸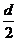 处,船渡河的速度为
处,船渡河的速度为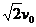
C. 小船渡河时的轨迹为直线
D. 小船到达离河岸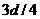 处,船的渡河速度为
处,船的渡河速度为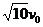
答案:A
例1. 如图1所示,人用绳子通过定滑轮以不变的速度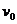 拉水平面上的物体A,当绳与水平方向成θ角时,求物体A的速度。
拉水平面上的物体A,当绳与水平方向成θ角时,求物体A的速度。

图1
解法一(分解法):本题的关键是正确地确定物体A的两个分运动。物体A的运动(即绳的末端的运动)可看作两个分运动的合成:一是沿绳的方向被牵引,绳长缩短。绳长缩短的速度即等于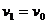 ;二是随着绳以定滑轮为圆心的摆动,它不改变绳长,只改变角度θ的值。这样就可以将
;二是随着绳以定滑轮为圆心的摆动,它不改变绳长,只改变角度θ的值。这样就可以将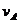 按图示方向进行分解。所以
按图示方向进行分解。所以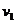 及
及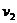 实际上就是
实际上就是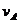 的两个分速度,如图1所示,由此可得
的两个分速度,如图1所示,由此可得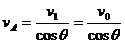 。
。
解法二(微元法):要求船在该位置的速率即为瞬时速率,需从该时刻起取一小段时间来求它的平均速率,当这一小段时间趋于零时,该平均速率就为所求速率。
设船在θ角位置经△t时间向左行驶△x距离,滑轮右侧的绳长缩短△L,如图2所示,当绳与水平方向的角度变化很小时,△ABC可近似看做是一直角三角形,因而有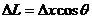 ,两边同除以△t得:
,两边同除以△t得: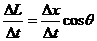
即收绳速率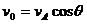 ,因此船的速率为:
,因此船的速率为:
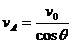
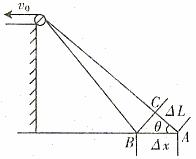
图2
总结:“微元法”。可设想物体发生一个微小位移,分析由此而引起的牵连物体运动的位移是怎样的,得出位移分解的图示,再从中找到对应的速度分解的图示,进而求出牵连物体间速度大小的关系。
解法三(能量转化法):由题意可知:人对绳子做功等于绳子对物体所做的功。人对绳子的拉力为F,则对绳子做功的功率为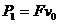 ;绳子对物体的拉力,由定滑轮的特点可知,拉力大小也为F,则绳子对物体做功的功率为
;绳子对物体的拉力,由定滑轮的特点可知,拉力大小也为F,则绳子对物体做功的功率为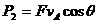 ,因为
,因为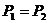 所以
所以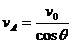 。
。
评点:①在上述问题中,若不对物体A的运动认真分析,就很容易得出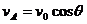 的错误结果;②当物体A向左移动,θ将逐渐变大,
的错误结果;②当物体A向左移动,θ将逐渐变大,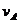 逐渐变大,虽然人做匀速运动,但物体A却在做变速运动。
逐渐变大,虽然人做匀速运动,但物体A却在做变速运动。
总结:解题流程:①选取合适的连结点(该点必须能明显地体现出参与了某个分运动);②确定该点合速度方向(物体的实际速度为合速度)且速度方向始终不变;③确定该点合速度的实际运动效果从而依据平行四边形定则确定分速度方向;④作出速度分解的示意图,寻找速度关系。
3. 能量方面:弹性碰撞动能守恒;非弹性碰撞动能不守恒;完全非弹性碰撞能量损失(不能完全恢复原形)最大。
注意:动量守恒定律的验证、分析推理、应用等实验中,不论在平面还是斜面或用其他方式进行,我们都要注意守恒的条件性。
解题原则:(1)碰撞过程中动量守恒原则;(2)碰撞后系统动能不增原则;(3)碰撞后运动状态的合理性原则。
碰撞过程的发生应遵循客观实际。如甲物追乙物并发生碰撞,碰前甲的速度必须大于乙的速度,碰后甲的速度必须小于、等于乙的速度或甲反向运动。
解决“追碰”问题大致分两类运动,即数学法(如函数极值法、图象法)和物理方法(参照物变换法、守恒法等)。
[模型演练]
如图2所示,一水平放置的圆环形刚性槽固定在桌面上,槽内嵌放着三个大小相同的刚性小球,它们的质量分别为m1、m2、m3、m2=m3=2m1,小球与槽的两壁刚好接触,而且它们之间的摩擦可以忽略不计。开始时,三球处于槽中I、II、III的位置,彼此间距离相等,m2和m3静止,m1以速度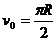 沿槽运动,R为圆环的内半径和小球半径之和,各球之间的碰撞皆为弹性碰撞,求此系统的运动周期T。
沿槽运动,R为圆环的内半径和小球半径之和,各球之间的碰撞皆为弹性碰撞,求此系统的运动周期T。
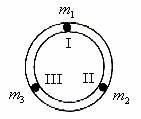
图2
答案:先考虑m1与m2的碰撞,令v1、v2分别为它们的碰后速度,由弹性正碰可得:
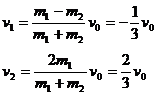
当m2与m3相碰后,交换速度,m2停在III处,m3以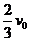 的速率运动。因为三段圆弧相等,当m3运动到位置I时,m1恰好返回。它们在I处的碰撞,m3停在I处,m1又以v0的速度顺时针运动。当m1再运动到II时,共经历了一个周期的
的速率运动。因为三段圆弧相等,当m3运动到位置I时,m1恰好返回。它们在I处的碰撞,m3停在I处,m1又以v0的速度顺时针运动。当m1再运动到II时,共经历了一个周期的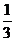 ,则:m1两次由位置I运动到II处的时间为:
,则:m1两次由位置I运动到II处的时间为: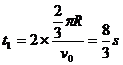 ,
, 由位置II运动到III处的时间为:
由位置II运动到III处的时间为: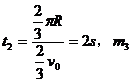 由位置III运动到I的时间为:
由位置III运动到I的时间为: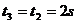 。
。
所以系统的周期为: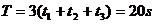
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com