
21. (本题12分)数列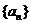 的前
的前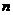 项和为
项和为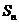 ,且
,且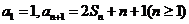 。
。
(1)求数列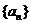 的通项公式;
的通项公式;
(2)设等差数列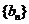 各项均为正数,满足
各项均为正数,满足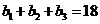 ,且
,且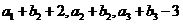 ,成等比数列。证明:
,成等比数列。证明: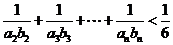 。
。
20. (本小题满分12分) 已知函数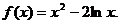
(I)求函数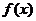 的单调递增区间;
的单调递增区间;
(II)若对任意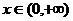 ,不等式
,不等式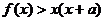 恒成立,求实数a的取值范围。
恒成立,求实数a的取值范围。
19. (本题12分) 如图,四面体ABCD中,
(本题12分) 如图,四面体ABCD中,
O、E分别是BD、BC的中点,
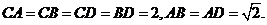
(I)求证: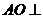 平面BCD;
平面BCD;
(II)求异面直线AB与CD所成角的大小;
(III)求点E到平面ACD的距离。
18.某公司招聘员工,指定三门考试课程,有两种考试方案.
方案一:考试三门课程,至少有两门及格为考试通过;
方案二:在三门课程中,随机选取两门,这两门都及格为考试通过.
假设某应聘者对三门指定课程考试及格的概率分别是0.5,0.6,0.9,且三门课程考试是否及格相互之间没有影响.求:
(Ⅰ)该应聘者用方案一考试通过的概率;
(Ⅱ)该应聘者用方案二考试通过的概率.
17.(本题10分)(本题12分) 已知函数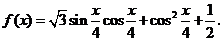
(1)求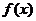 的单调递增区间;
的单调递增区间;
(2)在 中,角
中,角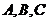 的对边分别是
的对边分别是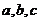 ,且满足
,且满足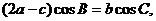 求函数
求函数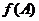 的取值范围.
的取值范围.
16. 已知圆M:(x+cosq)2+(y-sinq)2=1,
直线l:y=kx,下面四个命题:
(A) 对任意实数k与q,直线l和圆M相切;
(B) 对任意实数k与q,直线l和圆M有公共点;
(C) 对任意实数q,必存在实数k,使得直线l与和圆M相切
(D)对任意实数k,必存在实数q,使得直线l与和圆M相切
其中真命题的代号是______________(写出所有真命题的代号)
15. 过点(1,)的直线l将圆(x-2)2+y2=4分成两段弧,当劣弧所对的圆心角最小时,直线l的斜率k=
14.在(x4+)10的展开式中常数项是 (用数字作答)
13. 已知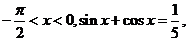 则
则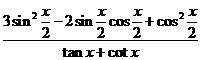 的值为
。
的值为
。
12. 已知an=(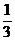 )n,把数列{an}的各项排列成如下的三角形状,
)n,把数列{an}的各项排列成如下的三角形状,
a1
a2 a3 a4
a5 a6 a7 a8 a9
…………………………
记A(m,n)表示第m行的第n个数,则A(10,12)=( )
A.(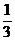 )93 B. (
)93 B. (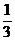 )92 C. (
)92 C. (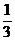 )94 D. (
)94 D. (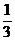 )112
)112
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com