
(1)动量守恒定律是说系统内部物体间的相互作用只能改变每个物体的动量,而不能改变系统的总动量,在系统运动变化过程中的任一时刻,单个物体的动量可以不同,但系统的总动量相同。
(2)应用此定律时我们应该选择地面或相对地面静止或匀速直线运动的物体做参照物,不能选择相对地面作加速运动的物体为参照物。
(3)动量是矢量,系统的总动量不变是说系统内各个物体的动量的矢量和不变。等号的含义是说等号的两边不但大小相同,而且方向相同。

规律方法 1、动量守恒定律的“四性”
在应用动量守恒定律处理问题时,要注意“四性”
①矢量性:动量守恒定律是一个矢量式,,对于一维的运动情况,应选取统一的正方向,凡与正方向相同的动量为正,相反的为负。若方向未知可设与正方向相同而列方程,由解得的结果的正负判定未知量的方向。
②瞬时性:动量是一个状态量,即瞬时值,动量守恒指的是系统任一瞬时的动量恒定,列方程m1vl+m2v2=m1v/l+m2v/2时,等号左侧是作用前各物体的动量和,等号右边是作用后各物体的动量和,不同时刻的动量不能相加。
③相对性:由于动量大小与参照系的选取有关,应用动量守恒定律时,应注意各物体的速度必须是相对于同一惯性参照系的速度,一般以地球为参照系
④普适性:动量守恒定律不仅适用于两个物体所组成的系统,也适用于多个物体组成的系统,不仅适用于宏观物体组成的系统,也适用于微观粒子组成的系统。
[例5]一辆质量为60kg的小车上有一质量为40kg的人(相对车静止)一起以2m/s的速度向前运动,突然人相对车以 4m/s的速度向车后跳出去,则车速为多大?
下面是几个学生的解答,请指出错在何处.
(1)解析;人跳出车后,车的动量为60v,人的动量为40(4十v)由动量守恒定律:
(60+40)×2=60v- 40(4+v)解得: v= 0.4 m/s (没有注意矢量性)
(2)解析:选车的方向为正,人跳出车后,车的动量为60v,人的动量一40×4,由动量守恒定律:
(60+40)×2=60v -40×4,解得v=6m/s (没有注意相对性)
(3)解析:选车的方向为正,人跳出车后的动量为60v,人的动量一40×(4一2)由动量守恒定律得
(60+40)×2=60v -40×(4一2)解得v=14/3m/s (没有注意瞬时性)
(4)解析:选地为参照物,小车运动方向为正,据动量守恒定律,
(60+40)×2=60v -40(4-v)解得 v=3.6m/s此法正确.答案:3.6 m/s
2、应用动量守恒定律的基本思路
3、 常见的表达式
不同的表达式及含义(各种表达式的中文含义):
P=P′ 或 P1+P2=P1′+P2′ 或 m1V1+m2V2=m1V1′+m2V2′
(其中p/、p分别表示系统的末动量和初动量,系统相互作用前的总动量P等于相互作用后的总动量P′)
ΔP=0 (系统总动量变化为0,或系统总动量的增量等于零。)
Δp1=-Δp2,(其中Δp1、Δp2分别表示系统内两个物体初、末动量的变化量,表示两个物体组成的系统,各自动量的增量大小相等、方向相反)。
如果相互作用的系统由两个物体构成,动量守恒的实际应用中具体来说有以下几种形式
A、m1vl+m2v2=m1v/l+m2v/2,各个动量必须相对同一个参照物,适用于作用前后都运动的两个物体组成的系统。
B、0= m1vl+m2v2,适用于原来静止的两个物体组成的系统。
C、m1vl+m2v2=(m1+m2)v,适用于两物体作用后结合在一起或具有共同的速度。
原来以动量(P)运动的物体,若其获得大小相等、方向相反的动量(-P),是导致物体静止或反向运动的临界条件。即:P+(-P)=0
2、 动量守恒定律适用的条件
守恒条件:①系统不受外力作用。 (理想化条件)
②系统受外力作用,但合外力为零。
③系统受外力作用,合外力也不为零,但合外力远小于物体间的相互作用力。
④系统在某一个方向的合外力为零,在这个方向的动量守恒。
⑤全过程的某一阶段系统受合外力为零,该阶段系统动量守恒,
即:原来连在一起的系统匀速或静止(受合外力为零),分开后整体在某阶段受合外力仍为零,可用动量守恒。
例:火车在某一恒定牵引力作用下拖着拖车匀速前进,拖车在脱勾后至停止运动前的过程中(受合外力为零)动量守恒
1、 内容:相互作用的物体系统,如果不受外力,或它们所受的外力之和为零,它们的总动量保持不变。即作用前的总动量与作用后的总动量相等.(研究对象:相互作用的两个物体或多个物体所组成的系统)
2、物体动量的增量可以是物体质量不变,由速度变化形成:ΔP=mv2I一mv1=m(V2一v1)=mΔv,
动量定理表达为FΔt=mΔv.也可以是速度不变,由质量变化形成:ΔP=m2v一mlv=(m2一ml)v=Δmv,动量定理表达为FΔt=ΔmV。在分析问题时要注意第二种情况。
 散
动量守恒定律
散
动量守恒定律
知识简析 一、动量守恒定律
1、动量定理FΔt=mvt-mv0可以用一种更简洁的方式FΔt=ΔP表达,
 式中左边表示物体受到的冲量,右边表示动量的增量(变化量)。此式稍加变形就得
式中左边表示物体受到的冲量,右边表示动量的增量(变化量)。此式稍加变形就得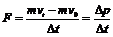
其含义是:物体所受外力(若物体同时受几个力作用,则为合外力)等于物体动量的变化率。这一公式通常称为“牛顿第二定律的动量形式”。这一形式更接近于牛顿自己对牛顿第二定律的表述。应用这个表述我们在分析解决某些问题时会使思路更加清晰、简洁。
2、动量定理的初步应用
注意:应用动量定理公式I=mv2一mvl时,不要把公式左边的冲量单纯理解为合外力的冲量,可以进一步理解为“外力冲量的矢量和”,这样就对全过程应用一次动量定理就可以解决问题而使思路和解题过程简化。
 散
动量定理的拓展应用
散
动量定理的拓展应用
5.用动量定理解题,只能选取地球或相对地球做匀速直线运动的物体做参照物。忽视冲量和动量的方向性,造成I与P正负取值的混乱,或忽视动量的相对性,选取相对地球做变速运动的物体做参照物,是解题错误的常见情况。
规律方法1、冲量和动量变化量的计算
点评:对力的冲量计算,学生比较习惯按做功的方法求,如IF易算为Fcosθt,而实际为Ft,对支持力、重力的冲量通常因为与位移垂直而认为是零。冲量和功不同。恒力在一段时间内可能不作功,但一定有冲量。对动量变化量,分不清应该用那个力的冲量来计算,实际只要求出合外力的冲量就可以了。
说明:(1)注意区别所求的是某一力的冲量还是合外力的冲量.
(2)恒力的冲量一般直接由I=Ft求,变力的冲量一般由I=ΔP求.
4.动量定理公式中的等号表明合外力的冲量与研究对象的动量增量的数值相等,方向一致,单位相同。但考生不能认为合外力的冲量就是动量的增量,合外力的冲量是导致研究对象运动改变的外因,而动量的增量却是研究对象受外部冲量作用后的必然结果。
3.动量定理公式中的Δ(mv)是研究对象的动量的增量,是过程终态的动量减去过程始态的动量(要考虑方向),切不能颠倒始、终态的顺序。
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com