
3. 探求线面平行的结果(性质)──“线面平行”是否意味着平行平面内的任一直线?只平行哪些线?
线面平行性质定理:如果一条直线和一个平面, 经过这条直线的平面和这个平面相交, 那么这条直线和交线平行.
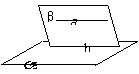

证明:a, b共面且没有公共点, 故平行.
强调:已知“线 // 面”时,过线作面得交线,化为“线 // 线”.
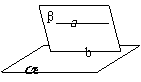
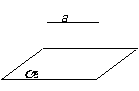
a // a  a // b
a // b
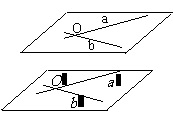
例:⑴己知平面α∩β= b, a//α, a //β, 求证:a // b.

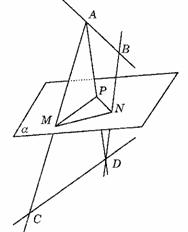
⑵异面直线AB、CD在平面α两侧, 都平行平面α,
若AC、BD与α交于M、N两点, 求证: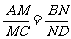 .
.
⑶三个平面两两相交, 求证三条交线交于一点或互相平行


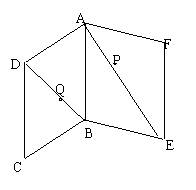
(4)有公共边AB而不共面的两矩形ABCD和ABEF中, P、Q分别
为对角线AE、BD上的点, 且AP=DQ, 求证:PQ//面CBE.
两个平面平行
4.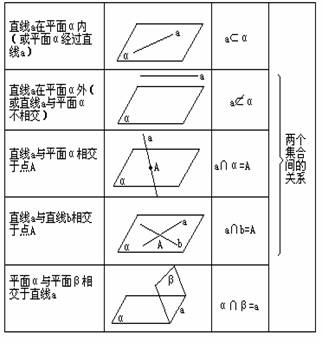 点、直线、平面之间的基本关系:
点、直线、平面之间的基本关系:
 把直线、平面看成是点的集合,借用集合中的符号语言来表示, 读法上仍用几何语言.
把直线、平面看成是点的集合,借用集合中的符号语言来表示, 读法上仍用几何语言.
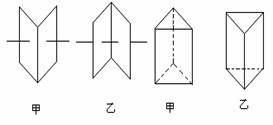 练习:观察图形,用模型来说明它们的位置有什么不同,并用字母表示各平面.
练习:观察图形,用模型来说明它们的位置有什么不同,并用字母表示各平面.
附注:讲评时,用书作示意,对直 线的可见部分与不可见部分加以区别.对可见棱与不可见棱加以区别.
练习:试用集合符号表示下列各语句,并画出图形:
(1)点A在平面α内,但不在平面β内;
(2)直线a经过不属于平面α的点A,且a不在平面α内;
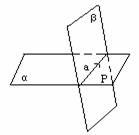
(3) 平面α与平面β相交于直线l,且l经过点P;(4)直线l经过平面α外一点P,且与平面α相交于点M.
平面的基本性质
公理1:如果一条直线上的两点在一个平面内,那么这条直线上所有的点都在这个平面内.
这时我们说直线在平面内,或者说平面经过直线.
 用集合符号表示:
用集合符号表示:
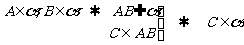 (证线、点在面内依据)
(证线、点在面内依据)
公理2:如果两个平面有一个公共点,那么它们有且只有一条通过这个点的公共直线.
用集合符号表示:P∈α, P∈βÞ α与β必相交 (证两平面相交依据)
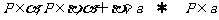 (证点在面内依据)
(证点在面内依据)
公理3: 经过不在同一条直线上的三个点,有且只有一个平面.
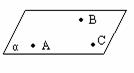 推论1: 经过一条直线和这条直线外一点,有且只有一个平面.
推论1: 经过一条直线和这条直线外一点,有且只有一个平面.
◈“有且只有一个平面”,我们也说“确定一个平面”.

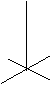

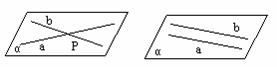 推论2: 经过两条相交直线,有且只有一个平面.(如图6)
推论2: 经过两条相交直线,有且只有一个平面.(如图6)
推论3: 经过两条平行直线,有且只有一个平面.(如图7)
◈应用平面的基本性质证明空间点和直线的共面问题.
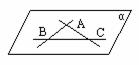 例:两两相交且不过同一点的三条直线必在同一个平面内.(如图8)
例:两两相交且不过同一点的三条直线必在同一个平面内.(如图8)
已知:AB∩AC=A,AB∩BC=B,AC∩BC=C.
求证:直线AB,BC,AC共面.
◈方法:证“空间的点、直线共面”可以先由某些元素确定一个平面,然后证明其它的元素也在这个面内.
小结:证“直线在平面内”只要证直线上有两点在平面内;
证“两个平面相交”只要证两平面有一个公共点;
证“点在平面内”可证该点在平面内的一条直线上;
证“点在直线上”可证点为两平面公共点, 直线上为两平面交线;
例:△ABC三边延长线与平面α分别交于D、E、F,求证:D、E、F在一条直线上.

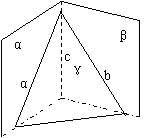
例:三平面α、β、γ相交如图, A、B∈α, C∈β,
试作出过ABC三点的平面与α、β、γ的交线.
 公理4:平行于同一条直线的两条直线互相平行.
公理4:平行于同一条直线的两条直线互相平行.
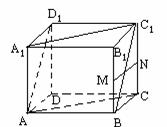
例:在正方体ABCD-A1B1C1D1中.
(1)AB与C1D1是什么位置关系?为什么?
(2)A1D1与BC是什么样的位置关系?为什么?
(3)如果M、N分别为B1B、C1C的中点,问A1D1与MN是什么位置关系?
(4)AC与A1C1是什么位置关系?为什么?
 (5)AD1与BC1是什么位置关系?为什么?
(5)AD1与BC1是什么位置关系?为什么?
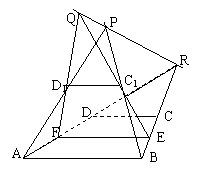
例: 梯形ABCD沿中位线EF折起成空间图形ABEC1D1F, 求证:
⑴AD1, BC1所在直线相交(记交点为P);
⑵设AD、BC交于R, EC1、FD1交于Q, 则P、Q、R三点共线.
等角定理:如果一个角的两边与另一个角的两边分别平行且方向相同,
则这两个角相等.
证明:构作两个三角形, 证全等.
思考:如果一个角的两边与另一个角的两边分别平行且方向相反呢?
如果一个角的两边与另一个角的两边分别平行且一组对应边同向另一组对应边反向呢?
推论:两条相交直线与另两条相交直线分别平行, 则两组相交直线所成的锐角或直角相等
注意:平面里的定义、定理等,对于非平面图形,需要经过证明才能应用
(1)“垂直于同一直线的两直线平行”在立体几何中不成立.
(2) “两组对边相等的四边形是平行四边形”在立体几何中不成立.
(3) “四边相等的四边形是菱形”在立体几何中不成立.
(4) “三个角是直角的四边形是矩形”这个平面几何中的定理在立体几何中也不成立, 可以发现“空间四边形四内角和小于360°”这是立体几何中的一个定理.
异面直线
 两直线位置关系:
两直线位置关系:
异面直线所成的角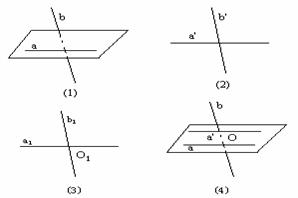 定义:直线a,b是异面直线,过空间任意一点O,分别引直线a′∥a,b′∥b,我们把直线a′和b′所成的锐角(或直角)叫做异面直线a和b所成的角.
定义:直线a,b是异面直线,过空间任意一点O,分别引直线a′∥a,b′∥b,我们把直线a′和b′所成的锐角(或直角)叫做异面直线a和b所成的角.
异面直线互相垂直:两条异面直线所成的角是直角
定理:一直线垂直于平行直线中的一条,也垂直于另一条.
异面直线所成的角θ角的取值范围:θ∈(0°,90°].
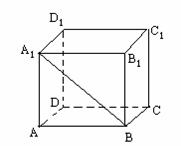 例:正方形ABCD-A1B1C1D1.求:
例:正方形ABCD-A1B1C1D1.求:
(1)A1B与CC1所成的角是多少度?为什么?
(2)A1B1与CC1所成的角是多少度?为什么?
(3)A1C1与BC所成的角是多少度?为什么?
(4)正方体ABCD-A1B1C1D1的棱中,与棱B1B垂直的棱有几条?
 定义:和两条异面直线都垂直相交的直线叫做两条异面直线的公垂线.
定义:和两条异面直线都垂直相交的直线叫做两条异面直线的公垂线.
异面直线的距离:两条异面直线的公垂线在这两条异面直线间的线段的长度,
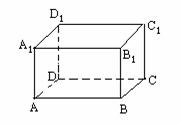
例:在长方体ABCD-A1B1C1D1中,AB=4cm,BC=3cm,B1B=2cm。求:
(1)异面直线A1A与BC的距离;
(2)异面直线A1A与C1D1的距离;
(3)异面直线A1B1与BC的距离.(如图)
例:正方体ABCD-A′B′C′D′的棱长为a.
(1)哪些棱所在的直线与直线BA′成异面直线?(证明两条直线是异面直线的方法有哪两个).
(2)求直线BA′和CC′所成的角的大小;
(3)求异面直线BC和AA′的距离.
直线和平面平行
 线面位置关系
线面位置关系


线面平行判定定理:平面外的一直线如果和平面内一直线平行, 则平行这个平面.
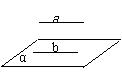
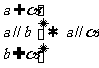
证明:反证法──可多种思路:⑴与公理4矛盾, ⑵与公理2矛盾, ⑶与a // b矛盾, (4)与a在α内矛盾
强调:⑴要证“线面平行”只要证“线线平行”;
⑵三个条件缺一不可. 提问:“一直线如果和平面内一直线平行, 则平行这个平面”正确吗?
例:(1). 空间四边形ABCD中, AB、AD中点分别为E、F, 求证EF//面BCD.
(2). 点P为平行四边形ABCD面外一点, PB中点为M, 求证PD//面MAC.
(3). 空间四边形ABCD中, P, Q分别是△ABC, △ADC的重心, 求证PQ//面BCD.
3.平面的表示法
⑴希腊字母α、β、γ前面加“平面”二字,如平面α等,且字母通常写在平行四边形的一个锐角内
⑵用平行四边形的四个字母表示,如平面ABCD
⑶用表示平行四边形的两个相对顶点的字母来表示,如平面AC.
2.平面的画法:通常画平行四边形来表示平面,被遮部分的线段画成虚线或不画。
注意:水平平面画两横边,横边为邻边的两倍,锐角画成45°;直立平面画两竖边.
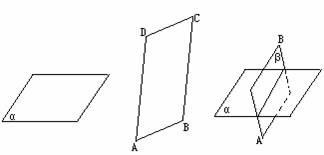
1.平面的特点:“平”、“无限延展”、“无厚薄”.
23.(1)北部 俄罗斯 乌拉尔山 太平洋 北冰洋 哈萨克斯坦 蒙古 中国(2)俄罗斯西可受大西洋影响,气候温和,为温和的大陆性气候,广大的西伯利亚地区冬冷夏温温差大,为温带大陆性气候,东部沿海地区受冬夏季风影响,为温带季风气候。(3)①石油和铁
③石油和天然气 ④煤和铁 (4)针叶 最广 (5)自给
22.(1)种植园(2)A,地中海 冬季温和湿润,夏季炎热干燥; B,温带海洋性 终年温和湿润 (3)AB
21.(1)波罗的海 北海 地中海 (2)温带海洋气候适宜牧草的生长 夏季地中海沿岸阳光明媚 (3)南部;葡萄酿酒业接近原料地 (4)工业小区;生产-销售-服务-
(5)②③④⑥;发展新兴工业和第三产业;发展科技 繁荣经济 (6)①②③④⑥;辽中南工业区;大连、鞍山、沈阳
23.读俄罗斯地图,完成下列要求:
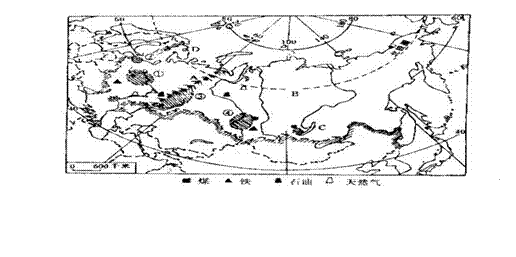 (图中①、②、③、④分别表示莫斯科工业区、圣比得堡工业区、乌拉尔工业区、新西伯利亚工业区)
(图中①、②、③、④分别表示莫斯科工业区、圣比得堡工业区、乌拉尔工业区、新西伯利亚工业区)
(1)北亚是指亚洲____ 地区,属于____ 的领土部分,它从____ 东麓向东延伸到____ 沿岸,北临____,南抵____ 、____、____的国界,是一个地广人稀的地区。
(2)分析说明俄罗斯东西气候的差异及其原因:____________________
。
(3)请对照图例,观察图中主要矿产,将这些工业区的主要矿产资源写在下列横线上:①______ _、 ③____ 、④____ 。
(4)俄罗斯是世界上亚寒带____ 林分布面积____ 的国家。
(5)俄罗斯矿产丰富,是世界上矿产资源能够________的少数国家之一。
[能力训练答案]
1-5 ABBCA 6-10DCCCD 11-15BAAAA 16-20BBCAC
22.读某国葡萄种植业分布示意图,回答下列问题。
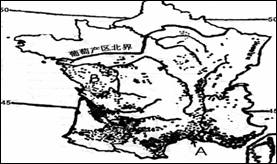
(1)该国葡萄种植业在农业的地域分类中属于 农业。
(2)说出葡萄种植区AB两地的气候类型及其特征。
A 气候,气候特征 ;
B 气候,气候特征 ;
(3)该国是欧洲最大的农产品出口国,目前农业可能面临的问题有( )
A.农业所需能源依赖进口,农业成本高
B.农业人口外流、老化现象严重, 后继乏人
C.因农业扩大再生产资金不足,难以形成规模效应
D.粮食生产受牧业、园艺业的冲击,粮食不能自给
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com