
1.已知:平面α∩平面β=直线l.A∈α,AB⊥β于B,BC⊥α于C.求证:AC⊥l.
4.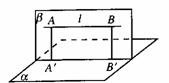 点面距离、线面距离──点与面、线与面有远近之别, 引入“距离”描述.
点面距离、线面距离──点与面、线与面有远近之别, 引入“距离”描述.
点到平面的距离:平面外一点向平面引垂线, 这个点和垂足间的距离(要作图).
例:如果一条直线和一个平面平行, 则这条直线上各点到平面的距离相等(线// 面性质).
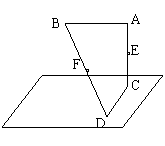 直线和平面的距离:一条直线和一个平面平行的, 直线上任一点到平面的距离(化归点面距离, 作图).
直线和平面的距离:一条直线和一个平面平行的, 直线上任一点到平面的距离(化归点面距离, 作图).
例:己知AB//面α, AC⊥α于C, BD∩α=D, AB⊥CD, AB=CD=4cm,
E、F分别为AC和BD中点, ⑴求证EF//α;⑵求EF的长.
例:已知:直线a∥平面α,直线b⊥平面α,求证:b⊥a.
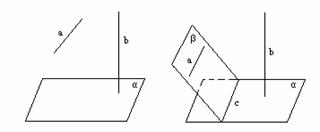
◈根据概念、定理作辅助线、辅助面, 动手作图前,脑中得先有有关概念和定理.
[补充题]
3.线面垂直性质定理:垂直于同一平面的两直线平行.
2.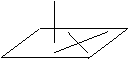 线面垂直判定定理:如果一条直线垂直一个平面内的两条相交直线, 则垂直这个平面.
线面垂直判定定理:如果一条直线垂直一个平面内的两条相交直线, 则垂直这个平面.
说明:⑴实质是由 “线⊥线”Þ“线⊥面”;⑵强调必须两线“相交”.
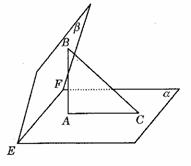
例:平面α∩β=EF, A∈α, AB⊥α, B∈β, BC⊥β, C∈α, 求证:⑴ EF⊥面ABC; ⑵ AC⊥EF

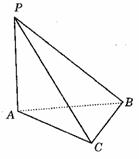
例:空间四边形ABCD中AB=BC, AD=CD, 求证:AC⊥BD.
例:己知PA⊥面ABC, AC⊥BC, 求证:BC⊥PC.
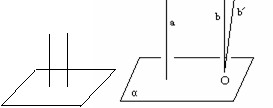
1.直线与平面互相垂直:直线和平面内的任意一条直线都垂直 ( 垂线l , 垂面α, 垂足A )
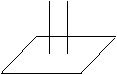
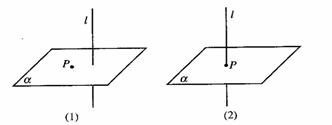
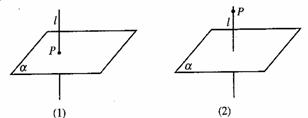 例:如果两条平行直线中的一条垂直于一个平面, 则另一条也垂直这个平面.
例:如果两条平行直线中的一条垂直于一个平面, 则另一条也垂直这个平面.
结论:过空间一点,有且只有一条直线与已知平面垂直,有且只有一个平面与已知直线垂直.
5. 平行平面间的距离──反映两个平行平面相隔远近.
两个平行平面的距离:夹在两个平行平面的公垂线段长度.
说明:⑴合理性:公垂线段的长度是唯一的.而且是夹在两个平行平面间的所有线段中最短的.
⑵转化思想:两平行平面的距离等于其中一个平面上的任一点到另一个平面的距离(垂线段长).
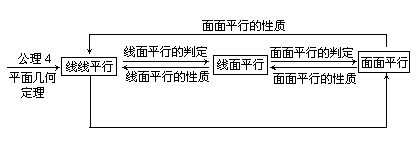 ◈小结:线线平行、线面平行与面面平行的判定定理和性质定理构成一套完整的定理体系.其内在的科学规律:低一级位置关系判定着高一级位置关系;高一级位置关系一定能推导低一级位置关系.
◈小结:线线平行、线面平行与面面平行的判定定理和性质定理构成一套完整的定理体系.其内在的科学规律:低一级位置关系判定着高一级位置关系;高一级位置关系一定能推导低一级位置关系.
直线与平面垂直
4.

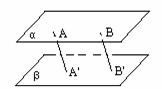
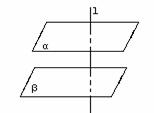 两个平面平行能推导出哪些正确的结论(性质)?
两个平面平行能推导出哪些正确的结论(性质)?
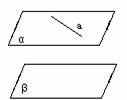
⑴ 两个平面平行, 其中一个平面内任一直线平行于另一平面;(“面//面”Þ“线//面”)
⑵ 如果两个平行平面同时和第三个平面相交,那么它们的交线平行;(“面//面”Þ“线//线”).
⑶ 一条直线垂直于两个平行平面中的一个平面,它也垂直于另一个平面(又一判定逆定理);
(4) 夹在两个平行平面间的平行线段相等.
面面平行的性质定理:如果两个平行平面同时和第三个平面相交,那么它们的交线平行;
说明:给出了在两个平行平面内找一对平行线的方法.即:“作一平面,交两面,得交线,则线线平行.”同时也给我们证明两条直线平行的又一方法.简言之,“面面平行,则线线平行”.
 例: 已知平面α∥β,AB,CD为夹在α,β间的异面线段,E、F分别为AB,CD的中点.
例: 已知平面α∥β,AB,CD为夹在α,β间的异面线段,E、F分别为AB,CD的中点.
求证:EF∥α,EF∥β.
3.
 又一判定定理:垂直于同一直线的两平面平行 .
又一判定定理:垂直于同一直线的两平面平行 .
证明:根据判定定理要构作辅助线──作面(用“同一平面内垂直于同 一直线的两直线平行”)
例:已知正方体ABCD-A1B1C1D1, 求证:平面AB1D1∥平面C1BD.

2. 两个平面平行的判定定理引入:
⑴若两平面平行,线面关系如何?
⑵反之,一个平面内的所有直线与另一平面都平行, 两平面平行吗?
⑶平面α内有一条直线与平面β平行,则α∥β,对吗?
平面α内有两条直线与平面β平行,则α∥β,对吗?
平面α内有无数条直线与平面β平行,则α∥β,对吗?
面面平行的判定定理:如果一个平面内有两条相交直线都平行于另一个平面, 则两个平面平行.
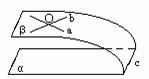 证明:作图、己知、求证(反证法, 结合“线//面Þ 线//线”)
证明:作图、己知、求证(反证法, 结合“线//面Þ 线//线”)
说明:⑴关键在于找到两相交直线都平行于另一个平面
⑵线//线 Þ 线//面 Þ 面//面.
⑶如果一个平面内两条相交直线分别平行于另一个平面内的两条相交直线,则两个平面平行.
1. 两个平面的位置关系小结引入:看公共点个数分类
线与线 ;线与面
;线与面 ;面与面
;面与面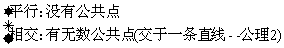
 画法与表示: α//β
α∩β=a
画法与表示: α//β
α∩β=a
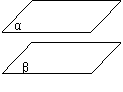
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com