
5.下列关于植物组织培养的叙述,不正确的是( )
A.利用植物体的花药进行植物组织培养可获得单倍体植株
B.植物组织培养成功的前提是选取离体的器官、组织或细胞
C.植物组织培养可用来制取人工种子,生产无毒苗
D.植物组织培养成功在整个过程需要光照,有利于叶绿素的合成和光合作用的进行
4.在对遗传病的分析研究中,常对患者及其亲属有丝分裂中期的染色体进行照相、放大、分组、比较分析。这是因为( )
A.中期的染色体包含两条染色单体
B.中期的染色体形态不再发生变化
C.中期的染色体形态固定,数目清晰,容易分析比较发现异常
D.中期持续时间最长,最容易找到中期细胞
3.下列关于胰岛素的有关说法,其中正确的是( )
A.胰岛素的合成需要线粒体供能
B.胰岛素可以用来治疗糖尿病,口服即可
C.通过与细胞膜相连的内质网将胰岛素分泌出去
D.胰岛素在胰岛A细胞中合成
2.乳酸菌和酵母菌相比较,相同之处是( )
A.在无氧环境中大量增殖 B.无各种细胞器
C.无成形的细胞核 D.遗传物质是DNA
1.下列实验中需要加热的是( )
A.鉴定还原糖 B.鉴定脂肪 C.DNA粗提取 D.鉴定蛋白质
3.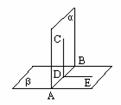 两个平面垂直的性质定理:如果两个平面垂直,在一个平面内垂直于它们交线
的直线垂直另一个平面
两个平面垂直的性质定理:如果两个平面垂直,在一个平面内垂直于它们交线
的直线垂直另一个平面
说明:“面面垂直”→“线面垂直”
例:如果两个平面垂直,那么经过第一个平面内的一点垂直于第二个平面的直线,
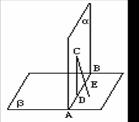 在第一个平面内.
在第一个平面内.
例:垂直于同一平面的两平面的交线垂直于这个平面.
已知:α⊥γ,β⊥γ,α∩β= a,求证:a⊥γ.

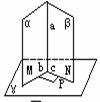
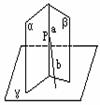
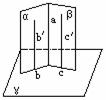
思考:在正三棱柱ABC-A1B1C1中,(正三棱柱指底面为正三角形,侧棱与底面垂直的三棱柱)E∈BB1,且BE=EB1, 求证:截面A1EC⊥侧面AC1.
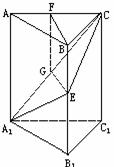
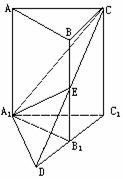
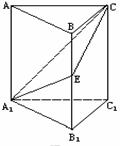
2.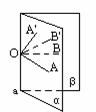 如何去度量二面角的大小呢?──将空间角化为平面角
如何去度量二面角的大小呢?──将空间角化为平面角
二面角的平面角: 以二面角的棱上任意一点为端点,在两个面内分别作垂直于棱的两条射线,这两条射线所成的角. 二面角的平面角是几度,就说这个二面角是几度.
三个主要特征是:⑴过棱上任意一点;⑵分别在两个面内作射线;⑶射线垂直于棱.
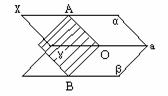

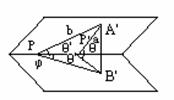
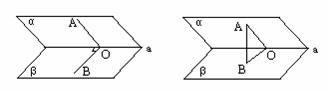 ◈作法:⑴按定义; ⑵利用三垂线定理; ⑶作垂面 (4)共底等腰△中线法
◈作法:⑴按定义; ⑵利用三垂线定理; ⑶作垂面 (4)共底等腰△中线法
 例:河堤坡面与水平面所成二面角是60°,堤面上有一条直道CD,它和坡脚的水平线AB的夹角是30°,沿这条路上堤,行走100米后人升高多少米?
例:河堤坡面与水平面所成二面角是60°,堤面上有一条直道CD,它和坡脚的水平线AB的夹角是30°,沿这条路上堤,行走100米后人升高多少米?
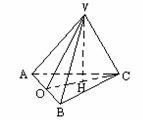 例:四面体V-ABC中,VA=VB=VC=a,AB=BC=CA=b,VH⊥面ABC,垂足为H,求侧面与底面所成的角的大小.
例:四面体V-ABC中,VA=VB=VC=a,AB=BC=CA=b,VH⊥面ABC,垂足为H,求侧面与底面所成的角的大小.
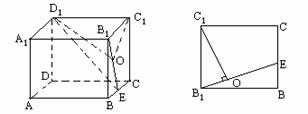 例:在正方体ABCD-A1B1C1D1中,棱长为2,E为BC的中点,求面B1D1E与面BB1C1C所成的二面角的大小的正切值.
例:在正方体ABCD-A1B1C1D1中,棱长为2,E为BC的中点,求面B1D1E与面BB1C1C所成的二面角的大小的正切值.
 例:矩形ABCD,AB=3,BC=4,沿对角线BD把△ABD折起,使点A在平面BCD上的射影A′落在BC上,求二面角A-BD-C的大小的余弦值.
例:矩形ABCD,AB=3,BC=4,沿对角线BD把△ABD折起,使点A在平面BCD上的射影A′落在BC上,求二面角A-BD-C的大小的余弦值.
◈解决平面图形折叠成立体图形的问题的关键在于搞清折叠前后的“变”与“不变”
[练习]
①在30°二面角的一个面内有一个点,它到另一个面的距离是a,求它到棱的距离.
②把边长为a的正方形ABCD以BD为轴折叠,使A-BD-C成60°的二面角,求A、C两点的距离.
3正四面体ABCD,求侧面与底面所成二面角的大小的余弦值.
4如果两个二面角的两个面对应平行,那么这两个二面角相等或互补.
 ⒉ 直二面角:平面角是直角的二面角.两个平面互相垂直:两个平面相交,所成的二面角是直二面角,
⒉ 直二面角:平面角是直角的二面角.两个平面互相垂直:两个平面相交,所成的二面角是直二面角,
两个平面垂直的判定定理:如果一个平面经过另一个平面的一条垂线,那么这两个平面互相垂直.
说明:“线面垂直”Þ“面面垂直”,关键是寻找在一个平面内的直线与另一平面垂直.
 例: 如图,正方体ABCD-A1B1C1D1中,E、F、G分别是A1B1,B1C1和BB1中点.求证:
例: 如图,正方体ABCD-A1B1C1D1中,E、F、G分别是A1B1,B1C1和BB1中点.求证:
(1)面ACC1⊥面BDD1B1;
(2)面ACFE⊥面BDD1B1;
(3)面ACG⊥面BDD1B1.
 例:设AB是⊙O的直径,P是平面⊙O外一点,PC⊥⊙O,C是⊙O上一点.
例:设AB是⊙O的直径,P是平面⊙O外一点,PC⊥⊙O,C是⊙O上一点.
求证:面PAC⊥面PBC.

思考:如图, 四边形BCDE是正方形,AB⊥面BCDE.
问图中所示7个平面中,共有多少个平面互相垂直?
1.概念
半平面:平面内的一条直线把平面分成两个半平面.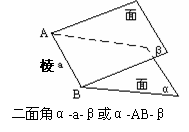
 二面角:从一条直线出发的两个半平面组成的图形.
二面角:从一条直线出发的两个半平面组成的图形.
可看作:一条射线绕其端点旋转形成的 一个半平面绕其界线旋转所得到的图形
5.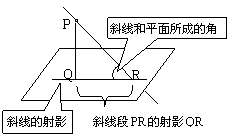 斜线在平面内的射影概念:
斜线在平面内的射影概念:


|
|
作图:在面α斜线上任取一点P作PQ⊥α于Q, 连结斜足R与垂足Q, 得射影RQ,
 则∠PRQ为斜线与平面所成的角(锐角).
则∠PRQ为斜线与平面所成的角(锐角).
补充:⑴“线⊥面”时, 线面角为90˚;
⑵“线Ì面”或“线//面”时, 线面角为0˚.
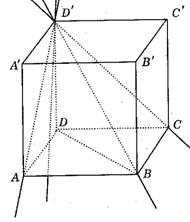
考察:正方体中底面与侧面的斜线、射影、线面角(如图)
◈定理:从平面外一点向该平面所引的垂线段和斜线段中:
 ⑴射影相等的两斜线段相等,
射影较长的斜线段也较长;
⑴射影相等的两斜线段相等,
射影较长的斜线段也较长;
⑵相等的斜线段的射影相等, 较长的斜线段射影也较长;
⑶垂线段比任何一条斜线段都短.
例:判断题 : ①两直线与平面所成的角相等,则这两条直线平行.( )
②平面的两斜线段相等, 则它们与平面所成的角也相等.( )
③过平面外一点引两条斜线段的射影相等, 则它们与平面所成的角相等.( )
④过平面外一点引两斜段与平面所成的角相等, 则斜线段也相等. ( )
5两条平行直线与同一平面成等角. ( )
例:面α的两斜线段PA、PB 在α内的射影分别为1和6, 与α所成的角相差45˚, 求点P到面α的距离.
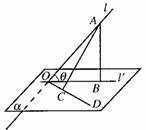
结论:⑴斜线与平面所成的角, 是这条斜线与这个平面内的直线所成的一切角中最小的角.
⑵如图,cos∠AOC=cos∠AOB﹒cos∠BOC .
[小结]
◈转化思想:“异面直线”化“相交直线”, “线//面”化“线//线”, “线⊥面”化“线⊥线”,
“线面距离”化“点面距离”, “线面角”化“线线角”等.
例:已知:在Rt△ABC中,∠ACB=90°,PB⊥平面ABC,BD⊥PC于D.
求证:(1)AC⊥BD;(2)BD⊥PA.
例:AB为异面直线a, b公垂线, l为平面α、β的交线, a⊥面α, b⊥面β, 求证AB // l.
例:AB为异面直线a, b公垂线, a //α, b //α, 则AB⊥α.
例:一条直线平行于一个平面, 则这条直线与这个平面的任意一条垂线垂直.
例:已知a // b // c, 设b、c所在平面为α, 且b、c相距28cm, b、a相距17cm, a、c相距15cm,
求a到面α距离.
两个平面垂直
2.已知:AB是圆O的直径,C是圆O上不同于A和B的点,PA⊥⊙O所在的平面.
求证:BC⊥PC.[提示:证明BC⊥平面PAC]
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com