
1.P=W/t 所求的是这段时间内平均功率.
4、做功求解的典型情况
①注意力、冲量、功的区别 除了它们的物理定义、单位以及是标量还是矢量以外,从动力学观点来看:
(1)力和物体的运动状态的变化存在着瞬时因果关系,即力是产生加速度的原因,有力才有加速度,力变加速度变,它们之间的因果规律用牛顿第二定律来表达.
(2)力的冲量反映的是力持续在一段时间的作用效果的累积量.其结果是要引起物体动量的改变,它们之间的因果规律用动量定理来表达.
(3)功是力持续作用在一段空间位移上的作用效果的累积量,是标量.其结果是要引起物体动能的改变,它们之间的因果规律用动能定理来表达.
②作用力和反作用力的做功
作用力与反作用力同时存在,作用力做功时,反作用力可能做功,也可能不做功,可能做正功,也可能做负功,不要以为作用力与反作用力大小相等、方向相反,就一定有作用力、反作用力的功数值相等,一正一负.所以作用力与反作用力做功不一定相等,但冲量的大小相等.
③摩擦力的做功
A、静摩擦力做功的特点
(1)静摩擦力可以做正功,也可以做负功,还可以不做功。
(2)在静摩擦力做功的过程中,只有机械能的相互转移(静摩擦力起着传递机械能的作用),而没有机械能转化为其他形式的能.
(3)相互摩擦的系统内,一对静摩擦力所做功的代数和总为零。
B.滑动摩擦力做功有以下的特点
(1)滑动摩擦力可以对物体做正功,也可以对物体做负功,当然也可以不做功。
(如相对运动的两物体之一对地面静止,则滑动摩擦力对该物不做功)
(2) 在相互摩擦的物体系统中,一对相互作用的滑动摩擦力做功的过程,,对物体系统所做总功的多少与路径有关,
能量的转化和转移的情况有两个方面:
一是 相互摩擦的物体通过摩擦力做功将部分机械能 转移另一个物体上,
转移另一个物体上,
其值是负值,等于摩擦力与相对路程的积,即Wf=f滑·S相对
二是 部分机械能 转化为内能,此部分能量就是系统机械能的损失量.
转化为内能,此部分能量就是系统机械能的损失量.
表示物体系统损失机械能克服了摩擦力做功,ΔE损= f滑·S相对=Q(摩擦生热).
一定要理解“摩擦生热”指的是滑动摩擦“生热,在相对滑动的过程中,通过摩擦力对系统做功来求解,必须求出摩擦力在相对路程上的功
(3)滑动摩擦力、空气摩擦阻力等,在曲线运动或往返运动时等于力和路程(不是位移)的乘积
如图所示,上面不光滑的长木板,放在光滑的水平地面上,一小木块以速度V0从木板的左端滑上木板,当木块和木板相对静止时,木板相对地面滑动了S,小木块相对木板滑动了d,则由动能定理知:
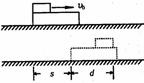 滑动摩擦力对木块所做功为: W木块=一f(d+S)……①
滑动摩擦力对木块所做功为: W木块=一f(d+S)……①
滑动摩擦力对木板所做功为: W木板=fs……②
所以,木块动能增量为: ΔEK木块=一f(d+s)……③
木板动能增量为: ΔEK木板=fs………④
由③④得:ΔEK木块+ΔEK木板=一fd………⑤
⑤式表明木块和木板组成的系统的机械能的减少量等于滑动摩擦力与木块相对木板的位移的乘积。这部分减少的能量转化为内能。
扩展与研究:
点评:求功的思路共有四条(1)由功的定义.恒力做功;(2)由能量关系求解;(3)由功率的定义;(4)由动能定理求解.
试题展示

功率
3、变力做功问题
 ①W=F·scosα是用来计算恒力的功,若是变力,求变力的功只有通过将变力转化为恒力,再用W=Fscosα计算.
①W=F·scosα是用来计算恒力的功,若是变力,求变力的功只有通过将变力转化为恒力,再用W=Fscosα计算.
②有两类不同的力:
一类是与势能相关联的力,比如重力、弹簧的弹力以及电场力等,它们的功与路径无关,只与始末点的位置有关;
另一类是滑动摩擦力、空气阻力等,在曲线运动或往返运动时,这类力(大小不变)功等于力和路程(不是位移)的积.
 ③根据功和能关系求变力的功.如:根据势能的变化求对应的力做的功,根据动能定理求变力做的功,等等.
③根据功和能关系求变力的功.如:根据势能的变化求对应的力做的功,根据动能定理求变力做的功,等等.
④根据功率恒定,求变力的功,W=Pt.
⑤求出变力F对位移的平均力来计算,当变力F是位移s的线性函数时,平均力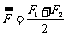 .
.
⑥作出变力F随位移,变化的图象,图象与位移轴所围均“面积”即为变力做的功.
2、多个力的总功求解
①用平行四边形定则求出合外力,再根据w=F合scosα计算功.注意α应是合外力与位移s间的夹角.
②分别求各个外力的功:W1=F1 scosα1, W2=F2scosα2……再求各个外力功的代数和.
 ①F:当F是恒力时,我们可用公式W=Fscosθ运算;当F大小不变而方向变化时,分段求力做的功;当F的方向不变而大小变化时,不能用W=Fscosθ公式运算(因数学知识的原因),我们只能用动能定理求力做的功.
①F:当F是恒力时,我们可用公式W=Fscosθ运算;当F大小不变而方向变化时,分段求力做的功;当F的方向不变而大小变化时,不能用W=Fscosθ公式运算(因数学知识的原因),我们只能用动能定理求力做的功.
②S:是力的作用点通过的位移,用物体通过的位移来表述时,在许多问题上学生往往会产生一些错觉,在后面的练习中会认识到这一点,另外位移S应当弄清是相对哪一个参照物的位移
③ 功是过程量:即做功必定对应一个过程(位移),应明确是哪个力在哪一过程中的功.
④ 什么力做功:在研究问题时,必须弄明白是什么力做的功.
点评:求功,必须清楚地知道是哪个力的功,应正确地画出力、位移,再求力的功.
规律方法 1、功的计算方法
1.由公式W=Fs cosα求解 (两种处理办法):
①W等于力F乘以物体在力F方向上的分位移scosα,即将物体的位移分解为沿F方向上和垂直F方向上的两个分位移
②W等于力F在位移s方向上的分力Fcosα乘以物体的位移s,即将力F分解为沿s方向和垂直s方向的两个分力
注意:这种方法只能用来计算恒力做功(轨迹可以是直线也可以是曲线)
9. 力的三种效果: 力的瞬时效应,改变物体的运动状态,产生加速成度.
力的三种效果: 力的瞬时效应,改变物体的运动状态,产生加速成度.
力的时间积累效应:使物体产生冲量,改变物体的动量. 是动量转化的量度
力的空间积累效应, 对物体做功, 改变物体的能量,是能的转化的量度
8.物理意义:表示力在空间上的积累效应,是能的转化的量度
7.功和能单位:焦耳(J) 1 J=1N·m. 1ev=1.6 10-19 J
6、两类不同的力做功求解的典型情况
一类是与势能相关的力,如重力、弹簧的弹力、电场力等,它们的功与路程无关系,只与位移有关。
另一类是滑动摩擦力,空气阻力等,这类力做功与物体的运动路径有关。滑动摩擦力做功要看物体运动的路程,这是摩擦力做功的特点,必须牢记。
5、力学中求功方法:
①公式求: W=FScosα(只适用于恒力做功,可分角力也可分角位移)
② W=Pt
③动能定理:W=EK2一Ek1,
④能量的转化情况求,(功是能量转达化的量度)
⑤F-s图象,图象与位移轴所围均“面积”为功的数值.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com