
2. 2007年9月14日,日本成功发射了月球探测卫星“月亮女神”, 其环月轨道高度为100km;10月24日中国成功发射了月球探测卫星“嫦娥一号”, 其环月轨道高度为200km,根据以上的已知条件,下列说法中正确是( )
A.“月亮女神”的周期小于“嫦娥一号”的周期
B.“月亮女神”的角速度小于“嫦娥一号”的角速度
C.“月亮女神”的加速度小于“嫦娥一号”的加速度
D.“月亮女神”的线速度小于“嫦娥一号”的线速度
单选题
1.关于地球同步卫星,下列说法正确的是( )
A. 卫星可以经过地球两极的正上方
B. 卫星质量越大,绕地球运行的速度就越大
C. 卫星的速度大于第一宇宙速度小于第二宇宙速度
D. 卫星绕地球运动的周期等于地球自转周期
21、本题有(1)、(2)、(3)三个小题,每题7分,请考生任选2题作答,满分14分,如果多做,则按所做的前两题计分。
(1)(选修4-2:矩阵与变换)
若点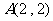 在矩阵
在矩阵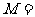

 对应变换的作用下得到的点为
对应变换的作用下得到的点为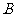
 ,求矩阵
,求矩阵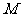 的逆矩阵.
的逆矩阵.
(2)(选修4-4:极坐标及参数方程)
已知曲线C的极坐标方程是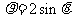 ,设直线l的参数方程是
,设直线l的参数方程是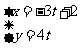 (t为参数).判断直线l和曲线C的位置关系.
(t为参数).判断直线l和曲线C的位置关系.
(3)(选修4-5:不等式选讲)
已知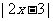 ≤1的解集为
≤1的解集为 ,若关于x的不等式
,若关于x的不等式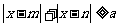 恒成立,求实数a的取值范围.
恒成立,求实数a的取值范围.
20、(本小题14分)已知函数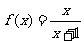 .
.
(1)求函数 的单调递增区间;
的单调递增区间;
(2)数列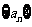 满足:
满足: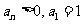 ,且
,且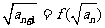 ,记数列
,记数列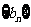 的前n项和为
的前n项和为 ,且
,且 ;试求:
;试求:
①求数列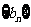 的通项公式;并判断
的通项公式;并判断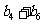 是否仍为数列
是否仍为数列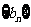 中的项?若是,请证明;否则,说
中的项?若是,请证明;否则,说
明理由.
②记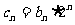 ,求数列
,求数列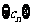 的前
的前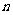 项和
项和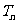 .
.
19、(本小题13分)已知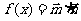 , 其中向量
, 其中向量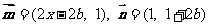 ,点
,点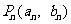 在
在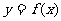 的图像上, 且点
的图像上, 且点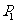 为
为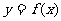 的图像与
的图像与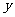 轴的交点.若数列
轴的交点.若数列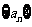 为等差数列, 且公差为1,
为等差数列, 且公差为1, 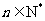 .
.
(1) 求数列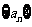 ,
, 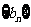 的通项公式;
的通项公式;
(2) 求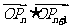 的最小值;
的最小值;
(3) 记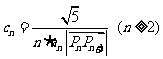 , 且
, 且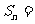
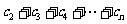 ,问是否存在
,问是否存在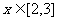 ,使得
,使得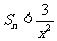 ?若存在,求出
?若存在,求出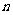 的值;若不存在,说明理由.
的值;若不存在,说明理由.
18、(本小题13分)如图,在棱长为2的正方体ABCD -A1B1C1D1中,E、F分别为AA1,和CC1的中点.
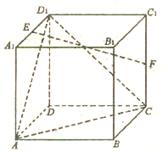 (1)求证:EF∥平面ACD1 ;
(1)求证:EF∥平面ACD1 ;
(2)求异面直线EF与AB所成角的余弦值;
(3)在棱BB1上是否存在一点P,使得二面角P-AC-B的大小
为30°?若存在,求出BP的长;若不存在,请说明理由.
17、(本小题13分)函数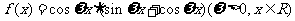 的图像与函数
的图像与函数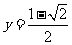 的图象的相邻两交点间的距离为
的图象的相邻两交点间的距离为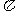 .
.
(1)求函数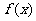 的解析式;
的解析式;
(2)若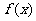 沿向量
沿向量 平移后的图像关于原点对称,求
平移后的图像关于原点对称,求 的最小值.
的最小值.
16、(本小题13分)已知函数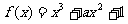 的图象在点B(1,
的图象在点B(1,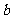 )处的切线的斜率为-3.
)处的切线的斜率为-3.
(1)求 、
、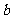 的值;
的值;
(2)若不等式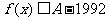 对于
对于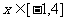 恒成立,求
恒成立,求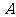 的取值范围.
的取值范围.
15、已知函数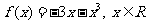 ,若
,若 时,不等式
时,不等式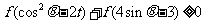 恒
恒
成立,则实数t的取值范围是 .
14、设两个向量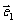 ,
,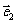 满足|
满足|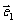 |=2,|
|=2,|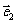 |=1,
|=1,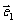 与
与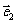 的夹角为
的夹角为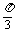 ,若向量
,若向量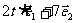 与
与 的
的
夹角为钝角,则实数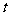 的范围是
.
的范围是
.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com