
3. 已知数列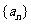 的前n项和
的前n项和 ,则
,则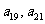 的符号
.
的符号
.
2. 求函数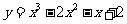 的零点个数 .
的零点个数 .
1. 方程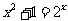 的解共有
.
的解共有
.
10.设平面直角坐标系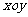 中,设二次函数
中,设二次函数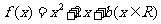 的图象与坐标轴有三个交点,经过这三个交点的圆记为C。(1)求实数
的图象与坐标轴有三个交点,经过这三个交点的圆记为C。(1)求实数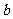 的取值范围;(2)求圆
的取值范围;(2)求圆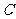 的方程
的方程
考点突破十六 函数与方程(2)
037函数方程的思想
[自我提醒]
(1) 函数和方程相互渗透。对于函数y=f(x),当y=0时,就转化为方程f(x)=0,也可以把函数式y=f(x)看做二元方程y-f(x)=0。函数问题(例如求反函数,求函数的值域等)可以转化为方程问题来求解,方程问题也可以转化为函数问题来求解,如解方程f(x)=0,就是求函数y=f(x)的零点。
(2) 函数、不等式相互转化。有关的不等式、方程、最小值和最大值之类的问题,利用函数观点加以分析。对于函数y=f(x),当y>0时,就转化为不等式f(x)>0,借助于函数图像与性质解决有关问题,而研究函数的性质,也离不开解不等式。
(3) 数列的通项或前n项和是自变量为正整数的函数,用函数的观点处理数列问题十分重要。等差、等比数列中,通项公式、前n项和的公式,都可以看成n的函数,数列问题也可以用函数方法解决。
(4) 实际应用问题,翻译成数学语言,建立数学模型和函数关系式,应用函数性质或不等式等知识解答。(5)遇到多元变量的数学问题中,选定合适的主变量,从而揭示其中的函数关系。
(6 解析几何中的许多问题,例如直线和二次曲线的位置关系问题,需要通过解二元方程组才能解决,涉及到二次方程与二次函数的有关理论。
(7立体几何中有关线段、角、面积、体积计算,经常需要运用布列方程或建立函数表达式方法加以解决。
[自我测试]
9.(2009福建卷文)若函数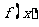 的零点与
的零点与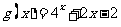 的零点之差的绝对值不超过0.25, 则
的零点之差的绝对值不超过0.25, 则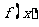 可以是
.
可以是
.
8.△ABC的三边a,b,c满足b+c=8, ,试确定△ABC的形状 .
,试确定△ABC的形状 .
7.递增数列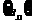 ,对任意正整数n,
,对任意正整数n,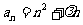 恒成立,求
恒成立,求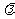 =
。
=
。
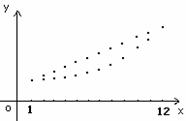
6.某厂2001年投资和利润逐月增加,投入资金逐月增长的百分率相同,利润逐月增加值相同。已知1月份的投资额与利润值相等,12月份投资额与利润值相等,则全年的总利润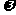 与总投资N大小关系
.
与总投资N大小关系
.
A、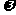 >N B
>N B  <N
C
<N
C  =N
D 不确定
=N
D 不确定
5.求函数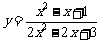 的值域
.
的值域
.
4.已知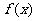 满足
满足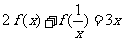 ,求
,求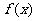 =
.
=
.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com