
14. 设实数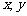 满足
满足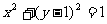 ,若对满足条件
,若对满足条件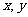 ,不等式
,不等式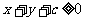 恒成立,则
恒成立,则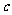 的取值范围是
的取值范围是
考点突破专题二十 常见的数学思想方法(6)
042放缩法、待定系数法
[自我提醒]
待定系数法:要确定变量间函数关系,设出某些未知系数,然后根据所给条件来确定这些未知系数的方法叫待定系数法,其理论依据是多项式恒等,也就是利用了多项式f(x)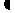 g(x)的充要条件是:对于一个任意的a值,都有f(a)
g(x)的充要条件是:对于一个任意的a值,都有f(a)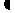 g(a);或者两个多项式各同类项的系数对应相等。
g(a);或者两个多项式各同类项的系数对应相等。
使用待定系数法,它解题的基本步骤是:第一步,确定所求问题含有待定系数的解析式
第二步,根据恒等的条件,列出一组含待定系数的方程;第三步,解方程组或者消去待定系数,从而使问题得到解决。
如何列出一组含待定系数的方程,主要从以下几方面着手分析:1。利用对应系数相等列方程;2。由恒等的概念用数值代入法列方程;3利用定义本身的属性列方程;4利用几何条件列方程;比如在求圆锥曲线的方程时,我们可以用待定系数法求方程:首先设所求方程的形式,其中含有待定的系数;再把几何条件转化为含所求方程未知系数的方程或方程组;最后解所得的方程或方程组求出未知的系数,并把求出的系数代入已经明确的方程形式,得到所求圆锥曲线的方程。
放缩法:为放宽或缩小不等式的范围的方法。常用在多项式中“舍掉一些正(负)项”而使不等式各项之和变小(大),或“在分式中放大或缩小分式的分子分母”,或“在乘积式中用较大(较小)因式代替”等效法,而达到其证题目的。所谓放缩的技巧:即欲证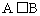 ,欲寻找一个(或多个)中间变量C,使
,欲寻找一个(或多个)中间变量C,使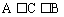 ,由A到C叫做“放”,由B到C叫做“缩”。
,由A到C叫做“放”,由B到C叫做“缩”。
常用的放缩技巧还有:(1)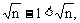
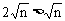
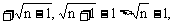
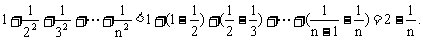
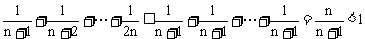
或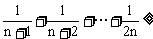
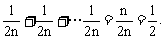
[自我测试]
13.(2009广东)已知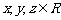 ,
,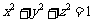 ,则
,则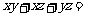
12. 实数a、b、c满足a+b+c=1,求a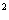 +b
+b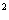 +c
+c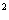 的最小值
。
的最小值
。
11.设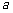 、
、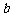 、
、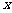 、
、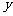 均为正数,且
均为正数,且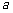 、
、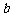 为常数,
为常数,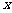 、
、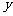 为变量.若
为变量.若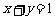 ,则
,则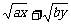 的最大值为
的最大值为
10.函数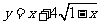 的值域
的值域
9.求函数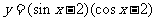 的最大、最小值
的最大、最小值
8. 求y=1+sinx+cosx+sinxcosx的值域
7.若函数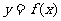 的值域是
的值域是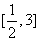 ,则函数
,则函数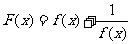 的值域是
的值域是
5.若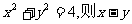 的最大值是
的最大值是
6函数 的值域
的值域
4.已知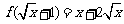 ,求
,求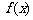 =
=
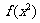 =
;
=
;
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com