
8.判断函数的奇偶性时,注意到定义域的特点了吗?(定义域关于原点对称是这个函数具有奇偶性的必要非充分条件)。奇函数的五个信息、偶函数的四条信息你都了解吗?
[自我测试]
7.求函数单调性时,易错误地在多个单调区间之间添加符号“∪”和“或”;单调区间是区间不能用集合或不等式表示。
5.求函数的单调区间,你考虑函数的定义域了吗?如求函数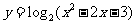 的单调增区间?6.函数单调性的证明方法是什么?(定义法、导数法)判定和证明是两回事呀!判断方法:定义法、图象法、利用常见函数的单调性及复合函数单调性的判断规则等。
还记得函数单调性与奇偶性逆用的例子吗?(⑴ 比较大小;⑵
解不等式;⑶ 求参数的范围。)
的单调增区间?6.函数单调性的证明方法是什么?(定义法、导数法)判定和证明是两回事呀!判断方法:定义法、图象法、利用常见函数的单调性及复合函数单调性的判断规则等。
还记得函数单调性与奇偶性逆用的例子吗?(⑴ 比较大小;⑵
解不等式;⑶ 求参数的范围。)
4.函数值域的一般求法你还记得吗?利用单调性、利用导数、利用函数的图像、利用判别式法、利用不等式的性质、利用常见函数的性质等。求值域与求最值不一样啊!求函数的最值,一般要指出取得最值时相应的自变量的值。求值域有哪些方法?你能够说出6种以上吗?(直接法,反函数法,配方法,换元法,均值不等式法,判别式法,单调性法,导数法)。分段函数怎么求值域?(分段求再综合)。分段函数怎么写表达式?(分段写,分别注明定义域,用大括号括起来);
14. 已知函数
已知函数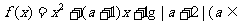 R,且
R,且 .
.
(I)若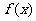 能表示成一个奇函数
能表示成一个奇函数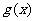 和一个偶函数
和一个偶函数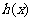 的和,求
的和,求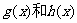 的解析式;
的解析式;
(II)命题P:函数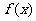 在区间
在区间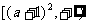 上是增函数;
上是增函数;
命题Q:函数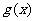 是减函数.
是减函数.
如果命题P、Q有且仅有一个是真命题,求a的取值范围;
考点突破专题二 初等函数与函数的应用(2)
004 函数性质:值域(最值)、定义域对称、奇偶性判定和性质、单调性判定和性质、凸凹性、对称性、周期性
[自我提醒]
13.已知函数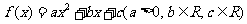 ,若函数
,若函数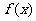 的最小值是
的最小值是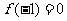 ,且
,且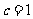 ,
,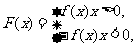 求
求 的值.
的值.
m
10. (安徽卷理11)若函数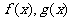 分别是
分别是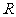 上的奇函数、偶函数,且满足
上的奇函数、偶函数,且满足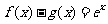 ,则
,则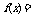
11(全国Ⅰ卷理6)若函数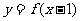 的图像与函数
的图像与函数 的图像关于直线
的图像关于直线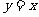 对称,则
对称,则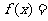 .
.
12 (江西卷文3)若函数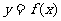 的定义域是
的定义域是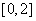 ,则函数
,则函数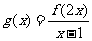 的定义域是
.
的定义域是
.
9.若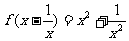 ,则函数
,则函数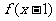 =
.
=
.
8. (山东卷文5)设函数 则
则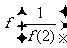 的值为
.
的值为
.
7.(浙江卷文11)已知函数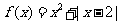 ,则
.
,则
.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com