第一节单项填空(共l5小题；每小题l分，满分l5分)

　　 从A、B、c、D四个选项中，选出可以填人空白处的最佳选项，并在答题卡上将该项涂

黑。

21. Late in the afternoon, they arrived at　　　　 small village　　　 north of the

　　 West Hill.

　　 A. the; the　　　　 B. a; 不填　 C. a; the　　　　 D. the; 不填

20．(本小题满分14分)

　　　 已知，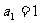

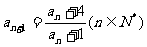
　 (1)求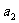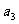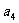，，的值；

　 (2)判断与2的大小关系，并证明你的结论；

　 (3)求证：≤.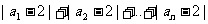

19．(本小题满分14分)

　　　 已知抛物线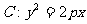，点P(-1，0)是其准线与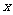轴的焦点，过P的直线与抛物线C交于A、B两点。

　 　(1)当线段AB的中点在直线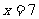上时，求直线的方程；

　 (2)设F为抛物线C的焦点，当A为线段PB中点时，求△FAB的面积。

18．(本小题满分13分)

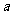　　　 设且≠0，函数.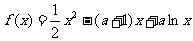

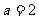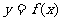　 (1)当时，求曲线在(3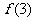，)处切线的斜率；

　 (2)求函数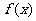的极值点。

17．(本小题满分13分)

　　　 已知集合，

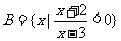
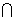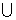　 (1)求AB，AB；

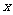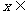　 (2)在区间(-4，4)上任取一个实数，求“A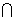B”的概率；

　 (3)设(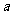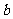，)为有序实数对，其中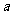是从集合A中任意的一个整数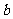，是从集合B中任取一个整数，求“ A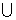B”的概率。

16．(本小题满分13分)

　　　 如图，在四棱锥P-ABCD中，底面ABCD是正方形，PD⊥底面ABCD，M、N分别为PA、BC的中点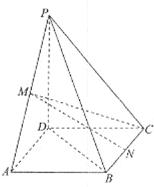，且PD=AD=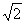，CD=1

　 (1)求证：MN∥平面PCD；

　 (2)求证：平面PAC⊥平面PBD；

　 (3)求三棱锥P-ABC的体积。

15．(本小题满分13分)

　　　 已知函数.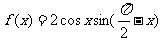

　 (1)求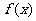的最小正周期；

　 (2)求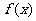在区间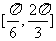上的最大值和最小值。

14．无穷等差数列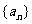的各项均为整数，首项为、

公差为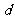，3、21、15是其中的三项，给出下列命题；

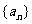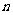
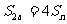　　　 ①存在满足条件的数列，使得对任意的N，成立。

②对任意满足条件的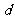，存在，使得99一定是数列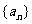中的一项；

③对任意满足条件的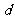，存在，使得30一定是数列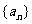中的一项；

其中正确命题为　　　　 。(写出所有正确命题的序号)