
1.用导数研究函数的单调性。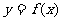 在区间
在区间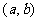 内可导,若
内可导,若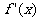 >0,则
>0,则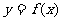 在
在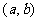 上递增;若
上递增;若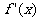 <0,则
<0,则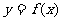 在
在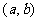 上递减. 注意:
上递减. 注意: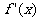 为正(负)是函数
为正(负)是函数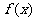 递增(减)充分不必要条件。如果函数f(x)在区间(a,b)内可导且不是常函数,上述结论可以改进为:f(x)在区间(a,b)上单调递增
递增(减)充分不必要条件。如果函数f(x)在区间(a,b)内可导且不是常函数,上述结论可以改进为:f(x)在区间(a,b)上单调递增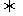
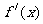 ≥0在(a,b)上恒成立;f(x)在区间(a,b)上单调递减
≥0在(a,b)上恒成立;f(x)在区间(a,b)上单调递减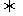
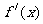 ≤0在(a,b)上恒成立
≤0在(a,b)上恒成立
[举例1]已知函数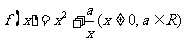 若
若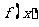 在
在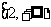 是增函数,求实数
是增函数,求实数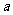 的范围。
的范围。
解析: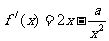 ≥0在
≥0在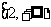 上恒成立
上恒成立
 在
在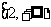 上恒成立
上恒成立
而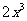 在
在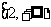 上的最小值为16,故
上的最小值为16,故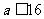 。
。
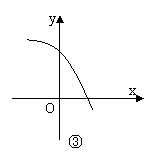
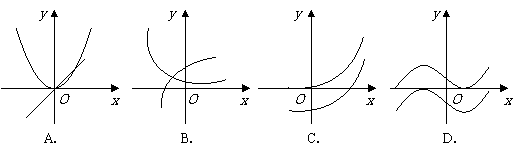
[举例2]已知定义在R上的函数y=f(x)的导函数f/(x)在R上也可导,且其导函数[f/(x)]/<0,
则y=f(x)的图象可能是下图中的 ( C )

 A.①② B.①③ C.②③ D.③④
A.①② B.①③ C.②③ D.③④
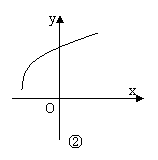
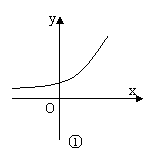
解析:由[f/(x)]/<0知f/(x)在R上递减,即函数y=f(x)的图象上从左到右各点处的切线斜率递减,不难看出图象②③满足这一要求。
[举例3] f(x)是定义在(0,+∞)上的非负可导函数,且满足xf/(x)+f(x)≤0,对任意正数a、b,若a<b,则必有 ( ) (07陕西理11)
A.af(b) ≤bf(a) B.bf(a) ≤af(b)
C.af(a) ≤f(b) D.bf(b) ≤f(a)
解析:xf/(x)+f(x)≤0 [xf(x)]/ ≤0
[xf(x)]/ ≤0 函数F(x)= xf(x) 在(0,+∞)上为常函数或递减,
函数F(x)= xf(x) 在(0,+∞)上为常函数或递减,
又0<a<b且f(x)非负,于是有:af(a)≥bf(b)≥0 ① 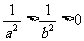 ②
②
①②两式相乘得: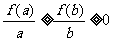
 af(b) ≤bf(a),故选A。
af(b) ≤bf(a),故选A。
注:本题的难点在对不等式②的设计,需要经验更需要灵感。
[巩固1]函数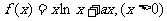 在
在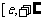 )上递增,
)上递增,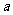 的取值范围是 。
的取值范围是 。
[巩固2设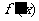 是函数
是函数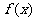 的导函数,将
的导函数,将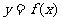 和
和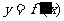 的图象画在同一个直角坐标系中,不可能正确的是( ) (07浙江理8)
的图象画在同一个直角坐标系中,不可能正确的是( ) (07浙江理8)
[巩固3]函数f(x)、g(x)在R上可导,且f/(x)>g/(x),若a>b,则 ( )
A.f(a)>g(b) B.g(a)<f(b)
C.f(a) -f(b) <g(a)- g(b) D.f(a) -f(b) >g(a)- g(b)
4、注意区分“求曲线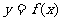 上过点M的切线”与“求曲线
上过点M的切线”与“求曲线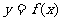 上在点M处的切线”;
上在点M处的切线”;
前者只要求切线过M点,M点未必是切点;而后者则很明确,切点就是M点。
[举例]求函数y=x3-3x2+x的图象上过原点的切线方程
解析:易见O(0,0)在函数y=x3-3x2+x的图象上,y’=3x2-6x+1,但O点未必是切点。
设切点A(x0,y0)∵y’=3x2-6x+1, ∴切线斜率为3x02-6x0+1,又切线过原点,∴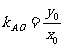 =3x02-6x0+1即:y0=3x03-6x02+x0 ①
=3x02-6x0+1即:y0=3x03-6x02+x0 ①
又∵切点A(x0,y0)y=x3-3x2+x的图象上∴y0=x03-3x02+x0 ②
由①②得:x0 =0或x0 =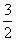 ,∴切线方程为:y=x或5x+4y=0
,∴切线方程为:y=x或5x+4y=0
点评:一般地,过三次曲线的对称中心(不难证明三次曲线一定是中心对称图形,且对称中心在曲线上)的切线有且仅有一条;而过三次曲线上除对称中心外的任一点的切线有二条。以下给出简单证明(不要求学生掌握):由于三次曲线都是中心对称曲线,因此,将其对称中心移至坐标原点便可将三次函数的解析式简化为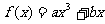 。若M(x1,y1)是三次曲线
。若M(x1,y1)是三次曲线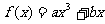 上的任一点,设过M的切线与曲线y=f(x)相切于(x0,y0),则切线方程为
上的任一点,设过M的切线与曲线y=f(x)相切于(x0,y0),则切线方程为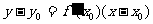 ,因点M上此切线上,故
,因点M上此切线上,故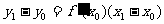 ,又
,又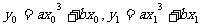 ,所以
,所以 ,整理得:
,整理得: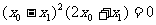 ,解得,
,解得,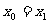 或
或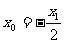 。 当点M是对称中心即
。 当点M是对称中心即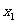 =
=
- =0时,过点M作曲线的切线切点是惟一的,且为M,故只有一条切线;当点M不是对称中心即
=0时,过点M作曲线的切线切点是惟一的,且为M,故只有一条切线;当点M不是对称中心即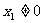 时,过点M作曲线的切线可产生两个不同的切点,故必有两条切线,其中一条就是以M为切点(亦即曲线在点M处)的切线。
时,过点M作曲线的切线可产生两个不同的切点,故必有两条切线,其中一条就是以M为切点(亦即曲线在点M处)的切线。
[巩固] 曲线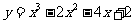 上过点
上过点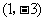 的切线方程是 .
的切线方程是 .
3.函数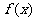 在
在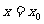 处的导数
处的导数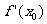 的几何意义:曲线
的几何意义:曲线 在其上点
在其上点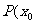 ,
,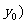 处的切线的斜率。用导数研究切线问题,切点是关键(切点在切线上、切点在曲线上、切点横坐标的导函数值为切线斜率)。
处的切线的斜率。用导数研究切线问题,切点是关键(切点在切线上、切点在曲线上、切点横坐标的导函数值为切线斜率)。
[举例1]曲线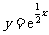 在点
在点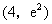 处的切线与坐标轴所围三角形的面积为( )
处的切线与坐标轴所围三角形的面积为( )
A.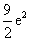 B.
B.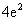 C.
C.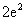 D.
D.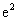 (07高考海南理10)
(07高考海南理10)
解析: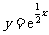

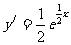 ,则]曲线在点
,则]曲线在点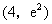 处的切线斜率为:
处的切线斜率为: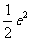 ,
,
∴切线方程为: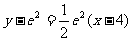 ,它与坐标轴的交点分别为:(2,0),(0,-
,它与坐标轴的交点分别为:(2,0),(0,-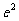 );
);
∴切线与坐标轴所围三角形的面积为: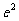 ,选D。
,选D。
[举例2]函数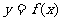 的图象在点P处的切线方程是:
的图象在点P处的切线方程是: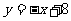 ,若点P的横坐标为5,
,若点P的横坐标为5,
则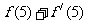 =
。
=
。
解析:本题没有函数表达式,但有切线方程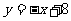 ,注意到“切点在切线上”,
,注意到“切点在切线上”,
∴P(5,3);又“切点在曲线上”,∴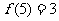 ;而曲线
;而曲线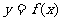 在点P处的切线斜率为
在点P处的切线斜率为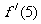 ,
,
即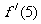 =-1,故
=-1,故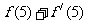 =2。
=2。
[举例3]已知直线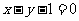 与抛物线
与抛物线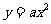 相切,则
相切,则
解析:本题固然可以将直线方程带入抛物线方程中,使得到的一元二次方程的判别式 =0,
=0,
从而求出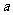 的值;但这种做法只限于二次曲线,若将抛物线换成其它的非二次曲线,则此路不通。以下用“导数”求解:“切点”是关键,记切点P(
的值;但这种做法只限于二次曲线,若将抛物线换成其它的非二次曲线,则此路不通。以下用“导数”求解:“切点”是关键,记切点P(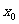 ,
,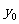 ),
),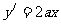 ,则有:
,则有:
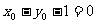 (切点在切线上)①;
(切点在切线上)①;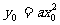 (切点在曲线上)②
(切点在曲线上)②
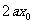 =1 (切点横坐标的导函数值为切线斜率)③;由①②③解得:
=1 (切点横坐标的导函数值为切线斜率)③;由①②③解得: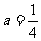 。
。
[巩固1]已知函数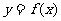 的图象在点
的图象在点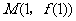 处的切线方程是
处的切线方程是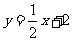 ,则
,则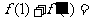 ____.(07高考湖北文13)
____.(07高考湖北文13)
[巩固2]点P是曲线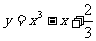 上的动点,设点P处切线的倾斜角为
上的动点,设点P处切线的倾斜角为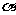 ,则
,则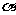 的取值范围是A、
的取值范围是A、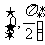 B、
B、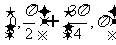 C、
C、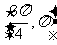 D、
D、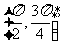
[巩固3]若直线y=x是曲线y=x3-3x2+ax的切线,则a=___________
2.常用导数公式: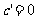 ,
,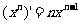 ,
,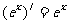 ,
,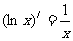 ;
;
导数的运算法则:若函数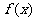 与
与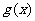 的导数存在,则
的导数存在,则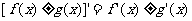 ,
,
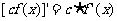 ,
, ;
;
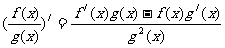 (这个公式很容易记错,注意和“积的导数”对比);
(这个公式很容易记错,注意和“积的导数”对比);
复合函数的导数:由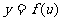 与
与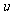 =
=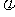
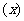 得到复合函数
得到复合函数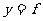
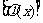 ,则
,则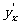 =
=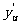 .
.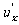 。
。
[举例1]已知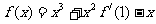 ,则
,则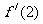 =
。
=
。
解析: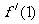 是常数,∴
是常数,∴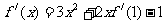

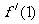 =3+2
=3+2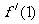 -1
-1
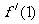 = -2
= -2
∴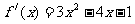 ,故
,故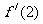 =3。
=3。
[举例2]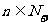 ,
,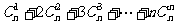 =
。
=
。
解析:本题可以用“倒序相加”法,也可以用“通项变化”法(k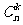 = n
= n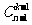 );这里,我们观察
);这里,我们观察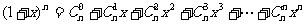 ①,不难发现其通项
①,不难发现其通项 求导后的系数正是所求“项”;故考虑对①式两边同求导数,得:
求导后的系数正是所求“项”;故考虑对①式两边同求导数,得:
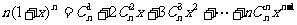 ,令
,令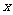 =1得:
=1得:
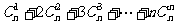 =
=
[巩固1] 已知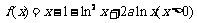 .令
.令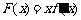 ,则
,则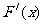 = 。
= 。
[巩固2]已知函数 ,则
,则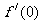 的值为:
的值为:
A.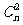 B.
B.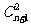 C.
C.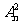 D.
D.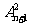
1.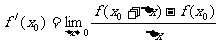 叫函数
叫函数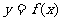 在
在 处的导数,记作
处的导数,记作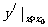 。
。
注:①函数应在点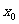 的附近有定义,否则导数不存在。②在定义导数的极限式中,
的附近有定义,否则导数不存在。②在定义导数的极限式中, 趋近于0可正、可负、但不为0,而
趋近于0可正、可负、但不为0,而 可能为0。③
可能为0。③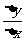 是函数
是函数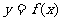 对自变量
对自变量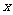 在
在 范围内的平均变化率,它的几何意义是过曲线
范围内的平均变化率,它的几何意义是过曲线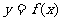 上点(
上点(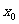 ,
,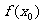 )及点(
)及点(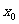 +
+ ,
,
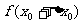 )的割线斜率。④导数
)的割线斜率。④导数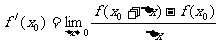 是函数
是函数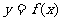 在点
在点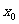 的处瞬时变化率,它反映的函数
的处瞬时变化率,它反映的函数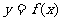 在
在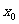 点处变化的快慢程度,它的几何意义是曲线
点处变化的快慢程度,它的几何意义是曲线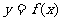 上点(
上点(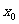 ,
,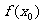 )处的切线的斜率。⑤若极限
)处的切线的斜率。⑤若极限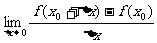 不存在,则称函数
不存在,则称函数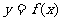 在点
在点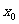 处不可导。⑥如果函数
处不可导。⑥如果函数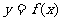 在开区间
在开区间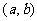 内每一点都有导数,则称函数
内每一点都有导数,则称函数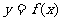 在开区间
在开区间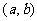 内可导;此时对于每一个
内可导;此时对于每一个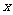 ∈
∈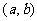 ,都对应着一个确定的导数
,都对应着一个确定的导数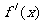 ,从而构成了一个新的函数
,从而构成了一个新的函数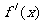 ,称这个函数
,称这个函数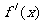 为函数
为函数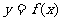 在开区间
在开区间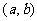 内的导函数,简称导数;导数与导函数都称为导数,这要加以区分:求一个函数的导数,就是求导函数;求一个函数在给定点的导数,就是求导函数值。
内的导函数,简称导数;导数与导函数都称为导数,这要加以区分:求一个函数的导数,就是求导函数;求一个函数在给定点的导数,就是求导函数值。
[举例1]若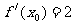 ,则
,则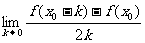 等于:
等于:
(A) -1 (B) -2 (C) 1 (D) 1/2
解析:∵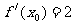 ,即
,即 =2
=2
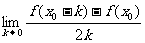 =-1。
=-1。
[举例2] 已知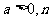 为正整数
为正整数 设
设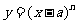 ,证明
,证明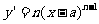
解析:本题可以对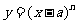 展开后“逐项”求导证明;这里用导数的定义证明:
展开后“逐项”求导证明;这里用导数的定义证明:
 =
=
 =
=
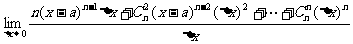 =
=
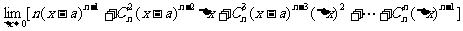 =
= 。
。
[巩固1]一质点作曲线运动,它的位移S与时间t的关系为: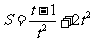 ,试用导数的定义求t =3时的速度。
,试用导数的定义求t =3时的速度。
[巩固2]设C是成本,q是产量,成本与产量的函数关系式为C=C(q),当产量为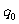 时,产量变化
时,产量变化 对成本的影响可用增量比
对成本的影响可用增量比 刻划. 如果
刻划. 如果 无限趋近于0时,
无限趋近于0时,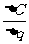 无限趋近于常数A,经济学上称A为边际成本. 它表明当产量为
无限趋近于常数A,经济学上称A为边际成本. 它表明当产量为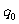 时,增加单位产量需付出成本A(这是实际付出成本的一个近似值)。设生产x个单位产品的总成本函数是C(x)=8+
时,增加单位产量需付出成本A(这是实际付出成本的一个近似值)。设生产x个单位产品的总成本函数是C(x)=8+ ,则生产8个单位产品时,边际成本是: ( )
,则生产8个单位产品时,边际成本是: ( )
A.2 B.8 C.10 D.16
25、14-16世纪的西欧文学与中国明末清初的文学都体现了反封建、追求个性解放的时代特征。下列作品能体现该特征的是( )
①《神曲》 ②《十日谈》 ③《三国演义》 ④《红楼梦》
A.①②③ B.①②④ C.②③④ D.①②③④
第Ⅱ卷(非选择题 共50分)
24、在下列自然科学成就中,影响远远超越其学科范围,扩展到社会和经济思想领域,并对中国近代民主思想产生了重要影响的是( )
A.经典力学 B.进化论 C.相对论 D.量子论
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com