
7.无穷数列{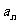 }的前n项和为Sn,
}的前n项和为Sn,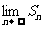 称为数列{
称为数列{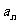 }的无穷多项和或所有项和。求
}的无穷多项和或所有项和。求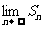 时,切不可分别求各项的极限后再求和;必须先求Sn,再求极限。若{
时,切不可分别求各项的极限后再求和;必须先求Sn,再求极限。若{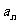 }为等比数列,公比为q且|q|<1,则
}为等比数列,公比为q且|q|<1,则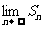 =
=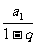 。
。
[举例1]若数列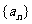 满足:
满足: 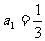 , 且对任意正整数
, 且对任意正整数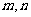 都有
都有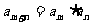 , 则
, 则
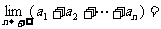 (07高考湖南理2)
(07高考湖南理2)
A.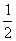 B.
B.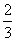 C.
C.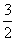 D.
D.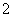
 解析:数列
解析:数列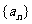 满足:
满足: 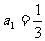 , 且对任意正整数
, 且对任意正整数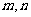 都有
都有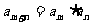 ,
,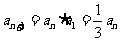 ,∴数列
,∴数列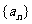 是首项为
是首项为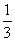 ,公比为
,公比为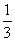 的等比数列。
的等比数列。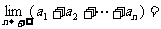
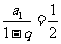 ,选A.
,选A.
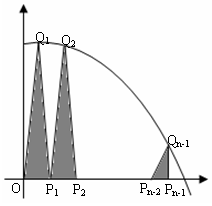
[巩固2]如图,抛物线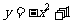 与
与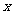 轴的正半轴交
轴的正半轴交
于点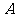 ,将线段
,将线段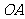 的
的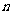 等分点从左至右依次记为
等分点从左至右依次记为
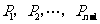 ,过这些分点分别作
,过这些分点分别作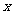 轴的垂线,
轴的垂线,
与抛物线的交点依次为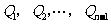 ,从而得到
,从而得到 个直角三角形
个直角三角形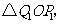
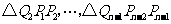 .当
.当 时,这些三角形的面积之和的极限为
.
时,这些三角形的面积之和的极限为
.
解析: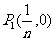 ,
,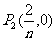 ,…,
,…,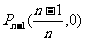 ;
;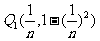 ,
,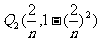 ,…,
,…, ,记
,记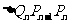 的面积为Sn,则S1=
的面积为Sn,则S1=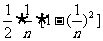 ,S2=
,S2=
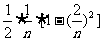 ,…,Sn-1=
,…,Sn-1=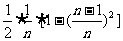 ;
; 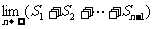 =
=
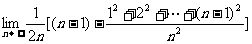 =
=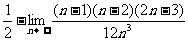 =
=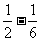 =
=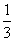 .
.
 [巩固1]数列{
[巩固1]数列{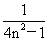 }的前n项和为Sn,则
}的前n项和为Sn,则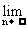 Sn=______________
Sn=______________
[巩固2] 如图,等边三角形ABC的面积等于1,连结这个三角形各边的中
点得到一个小三角形,又连结这个小三角形各边的中点得到一个更小的
三角形,如此无限继续下去,求所有这些三角形的面积的和.
[巩固3]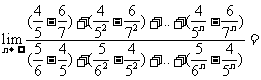 _____________
_____________
6.若|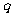 |<1,则
|<1,则
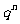 =0;
=0;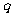 =1,则
=1,则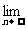
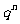 =1;若
=1;若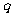 >1或
>1或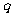 ≤-1, 则
≤-1, 则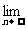
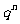 不存在。
不存在。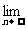
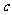
=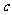 (
(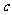 为常数);“
为常数);“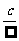 ”型的式子极限为0;“
”型的式子极限为0;“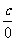 ”型、“
”型、“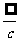 ”型的极限不存在;“
”型的极限不存在;“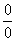 ”型和“
”型和“ ”型,一般分子、分母“同除以”一个式子(包括“约分”)后再求极限;含有根式的和(差)的式子一般有理化后再求极限。若
”型,一般分子、分母“同除以”一个式子(包括“约分”)后再求极限;含有根式的和(差)的式子一般有理化后再求极限。若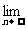
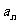 =A、
=A、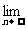
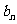 =B,则
=B,则 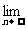 (
(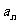 ±
±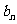 )=
A±B,
)=
A±B, 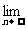 (
(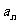
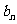 )=AB,
)=AB, 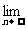
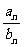 =
=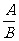 (B≠0).
(B≠0).
[举例1]若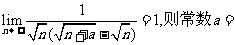 .
.
解析:分母有理化
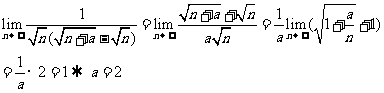
[举例2]已知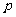 和
和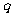 是两个不相等的正整数,且
是两个不相等的正整数,且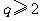 ,则
,则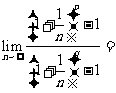 ( )
( )
A.0 B.1 C.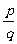 D.
D.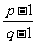 (07高考湖北理5)
(07高考湖北理5)
解析:
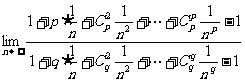
=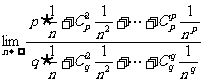 =
=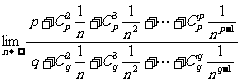 =
=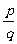 ,选C。
,选C。
[巩固1]把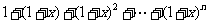 展开成关于
展开成关于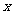 的多项式,其各项系数和为
的多项式,其各项系数和为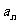 ,则
,则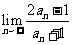 等于( )
等于( )
A.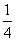 B.
B.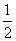 C.
C.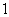 D.2
D.2
[巩固2]. n→∞lim等于( )
A. 1 B. C. D.0
[迁移]设正数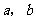 满足
满足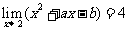 ,则
,则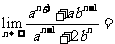 ( )
( )
A.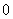 B.
B.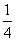 C.
C.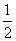 D.
D.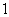 (07高考重庆理8)
(07高考重庆理8)
5.若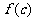 存在,则
存在,则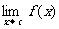 =
=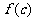 ,若
,若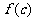 =
=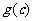 =0,则
=0,则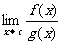 一般“约分”(约去含
一般“约分”(约去含 的因式)后再求极限。若
的因式)后再求极限。若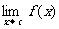 =A、
=A、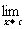
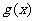 =B,则
=B,则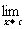 [
[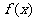 ±
±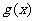 ]= A±B,
]= A±B, 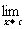 [
[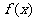
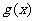 ]=AB,
]=AB, 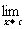
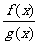 =
=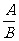 (B≠0).
(B≠0).
[举例] 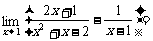 .(07高考陕西理13)
.(07高考陕西理13)
解析: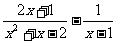 =
=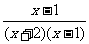 =
=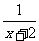 ,
,
∴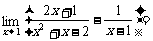
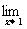
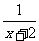 =
=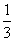
[巩固1] 下列四个命题中,不正确的是( )
A.若函数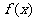 在
在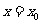 处连续,则
处连续,则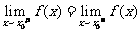
B.函数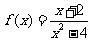 的不连续点是
的不连续点是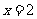 和
和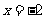
C.若函数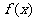 ,
,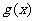 满足
满足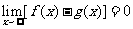 ,则
,则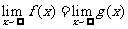
D.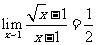 (07高考湖南理7)
(07高考湖南理7)
[巩固2] 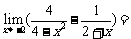 ________
________
4.数学归纳法通常用于证明关于自然数n的等式、不等式、整除性等。用“归纳假设”即命题p(k)成立证明命题 p(k+1)成立(已知p(k)成立,求证p(k+1)成立)是数学归纳法证明中最关键的一步;而明晰命题p(k)与命题 p(k+1)之间的关系又是实现这一步的前提。
[举例1] 已知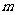 为正整数,用数学归纳法证明:当
为正整数,用数学归纳法证明:当 时,
时,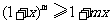 ;
;
解析:视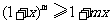 为关于
为关于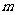 的不等式,
的不等式,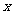 为参数,以下用数学归纳法证明:
为参数,以下用数学归纳法证明:
(ⅰ)当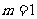 时,原不等式成立;当
时,原不等式成立;当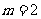 时,左边
时,左边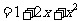 ,右边
,右边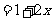 ,
,
因为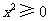 ,所以左边
,所以左边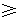 右边,原不等式成立;
右边,原不等式成立;
(ⅱ)假设当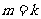 时,不等式成立,即
时,不等式成立,即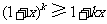 ,则当
,则当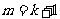 时,
时,
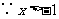 ,
, ,于是在不等式
,于是在不等式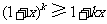 两边同乘以
两边同乘以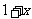 得
得
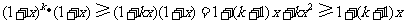 ,
,
所以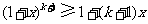 .即当
.即当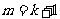 时,不等式也成立.
时,不等式也成立.
综合(ⅰ)(ⅱ)知,对一切正整数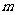 ,不等式都成立.
,不等式都成立.
[举例2]设正整数数列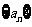 满足:
满足: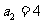 ,且对于任何
,且对于任何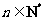 ,有
,有
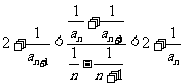 ;(1)求
;(1)求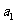 ,
,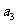 ;(2)求数列
;(2)求数列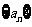 的通项
的通项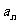 .
.
(07高考江西理22)
解析:(1)据条件得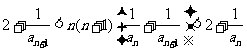 ①
①
当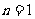 时,由
时,由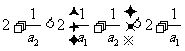 ,即有
,即有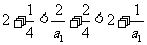 ,
,
解得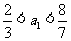 .因为
.因为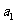 为正整数,故
为正整数,故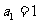 .
.
当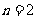 时,由
时,由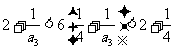 ,解得
,解得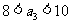 ,所以
,所以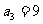 .
.
(2)由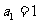 ,
,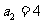 ,
,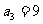 ,猜想:
,猜想: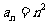 .
.
下面用数学归纳法证明.
1 当
当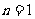 ,
, 时,由(1)知
时,由(1)知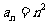 均成立;
均成立;
2 假设
假设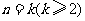 成立,则
成立,则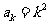 ,则
,则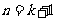 时
时
由①得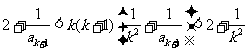
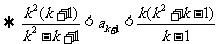
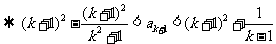
因为 时,
时,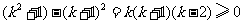 ,所以
,所以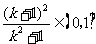 .
.
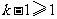 ,所以
,所以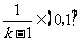 .又
.又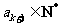 ,所以
,所以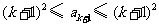 .
.
故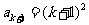 ,即
,即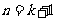 时,
时,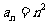 成立.由1
成立.由1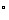 ,2
,2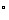 知,对任意
知,对任意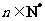 ,
,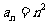 .
.
[巩固1]已知数列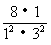 ,
,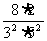 ,…,
,…,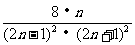 ,…;S
,…;S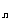 为其前n项和,求S
为其前n项和,求S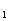 、S
、S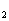 、S
、S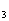 、S
、S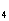 ,推测S
,推测S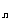 ,并用数学归纳法证明。
,并用数学归纳法证明。
[巩固2] 已知各项均为正数的数列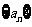 的前
的前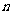 项和
项和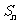 满足
满足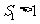 ,且
,且 ,
,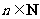 .(Ⅰ)求
.(Ⅰ)求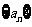 的通项公式;
的通项公式;
(Ⅱ)设数列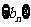 满足
满足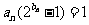 ,并记
,并记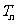 为
为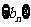 的前
的前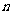 项和,求证:
项和,求证:
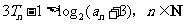 (07高考重庆理21)
(07高考重庆理21)
3.数学归纳法公理:如果关于自然数n 的一个命题p(n)满足下列条件 (1) p(n0)成立,即当n=n0时,命题成立,(2) 假设p(k)成立,则p(k+1)也成立;根据(1)(2)知命题p(n)对n≥n0的所有自然数n都成立。用数学归纳法证明问题的过程实质上是一个递推的过程,(1)是递推的基础,(2)是递推的条件;二者缺一不可。
2.能根据f(k)正确写出f(k+1),并能指出f(k)与f(k+1)之间的关系,这往往是运用数学归纳法的最关键的一步。
[举例1]已知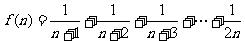 ,则
,则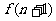 =
=
A.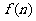 +
+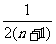 ,
B.
,
B.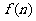 +
+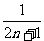 +
+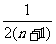 ,
,
C.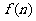 -
-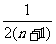 D.
D.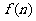 +
+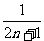 -
-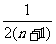
解析: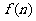 是从n+1开始的n个连续自然数的倒数和,故
是从n+1开始的n个连续自然数的倒数和,故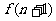 是从n+2开始的n+1个连续自然数的倒数和,即
是从n+2开始的n+1个连续自然数的倒数和,即
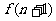 =
=
=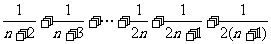 =
=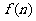 +
+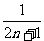 +
+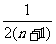 -
-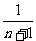
=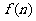 +
+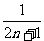 -
-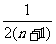 故选D。
故选D。
[举例2]用数学归纳法证明“5n-2n能被3整除”的第二步中,n=k+1时,为了使用归纳假设,应将5k+1-2k+1变形为
[解析]假设n=k时命题成立.即:5k-2k 被3整除.当n=k+1时,5k+1-2 k+1 =5×5k-2×2 k
=5(5k-2k) +5×2k-2×2k=5(5k-2k) +3×2k
[巩固1] 用数学归纳法证明1+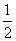 +
+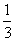 +…+
+…+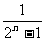 <n (n>1)时,由n=k (k>1)不等式成立,推证n=k+1时,左边应增加的代数式的个数是_____。
<n (n>1)时,由n=k (k>1)不等式成立,推证n=k+1时,左边应增加的代数式的个数是_____。
A. 2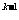 B. 2
B. 2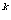 -1 C. 2
-1 C. 2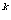 D. 2
D. 2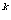 +1
+1
[巩固2]用数学归纳法证明命题:
(n+1) ×(n+2) ×…×(n+n)=2n×1×3×…×(2n-1)
1.数学归纳法用于证明一个“关于正自然数n的命题对于从正自然数n0开始的所有正自然数n都成立”的问题。
4.复数包括实数和虚数,实数是虚部为0的复数;-1的“平方根”为 ,
,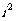 = -1,
= -1,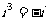 ,
,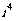 =1,
=1,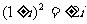 ;复数运算遵循有理式的运算法则;复数的商一般将分母“实数化”(分子分母同乘分母的共扼复数);两个虚数不能比较大小;两个复数相等当且仅当它们的实部相等,虚部也相等;复数
;复数运算遵循有理式的运算法则;复数的商一般将分母“实数化”(分子分母同乘分母的共扼复数);两个虚数不能比较大小;两个复数相等当且仅当它们的实部相等,虚部也相等;复数 (
(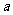 ∈R,
∈R,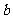 ∈R)在复平面内唯一对应点(
∈R)在复平面内唯一对应点(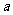 ,
,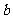 )。
)。
[举例1] 设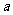 是实数,且
是实数,且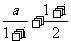 是实数,则
是实数,则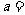 ( )
( )
A.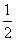 B.
B.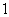 C.
C.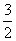 D.
D.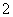
解析: =
=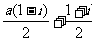 =
=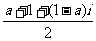 ∈R,则
∈R,则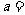 1
1
[举例2] 已知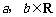 ,且
,且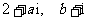 (
(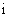 是虚数单位)是实系数一元二次方程
是虚数单位)是实系数一元二次方程
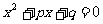 的两个根,那么
的两个根,那么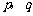 的值分别是( )A
的值分别是( )A
A.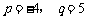 B.
B.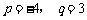
C.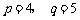 D.
D.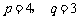
解析:分别将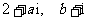 代入方程得:
代入方程得: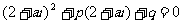 ①
①
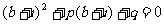 ②
对①②整理得:
②
对①②整理得:
 ;解得:
;解得: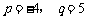 。本题也可以用“韦达定理”求解:
。本题也可以用“韦达定理”求解:
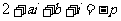 ③,
③, ④ 对③④整理得:
④ 对③④整理得:


 。
。
[巩固1]在复平面内,复数z=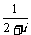 对应的点位于
对应的点位于
(A)第一象限 (B)第二象限 (C)第在象限 (D)第四象限
[巩固2] 设复数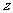 满足
满足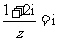 ,则
,则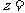 ( )
( )
A.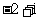 B.
B.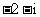 C.
C. D.
D.
3.求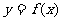 在闭区间内的最值的步骤:(1)求导数
在闭区间内的最值的步骤:(1)求导数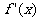 (2)求导数方程
(2)求导数方程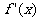 =0的根(3)检查
=0的根(3)检查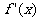 在根的左右值的符号,列表求得极值;也可通过解不等式
在根的左右值的符号,列表求得极值;也可通过解不等式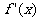 ≥0及
≥0及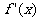 ≤0确定函数
≤0确定函数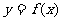 在给定区间内的单调情况,再确定函数的极值;最后将极值与区间端点的函数值比较以确定最值。
在给定区间内的单调情况,再确定函数的极值;最后将极值与区间端点的函数值比较以确定最值。
[举例1] 设函数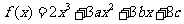 在
在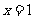 及
及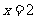 时取得极值.
时取得极值.
(Ⅰ)求a、b的值;(Ⅱ)若对于任意的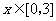 ,都有
,都有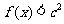 成立,求c的取值范围.
成立,求c的取值范围.
解析:(Ⅰ)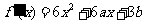 ,由
,由 ,
, .解得
.解得 ,
,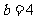 .
.
(Ⅱ)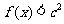 在[0,3]上恒成立即
在[0,3]上恒成立即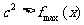 ,
,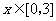
由(Ⅰ)可知,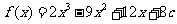 ,
,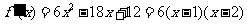 .
.
当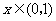 时,
时,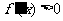 ;当
;当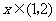 时,
时,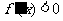 ;当
;当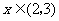 时,
时,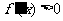 .
.
即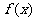 在
在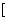 0,1]上递增,[1,2]上递减,[2,3]上递增;∴当
0,1]上递增,[1,2]上递减,[2,3]上递增;∴当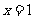 时,
时,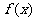 取得极大值
取得极大值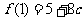 ,又
,又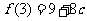 .故当
.故当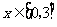 时,
时,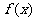 的最大值为
的最大值为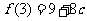 .
.
于是有: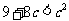 ,解得
,解得 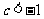 或
或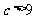 ,因此
,因此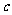 的取值范围为
的取值范围为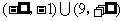 。
。
[举例2] 已知定义在正实数集上的函数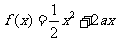 ,
,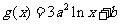 ,其中
,其中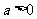 .设两曲线
.设两曲线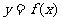 ,
,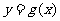 有公共点,且在该点处的切线相同.用
有公共点,且在该点处的切线相同.用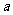 表示
表示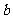 ,并求
,并求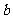 的最大值;
的最大值;
解析:设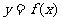 与
与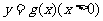 在公共点
在公共点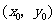 处的切线相同.
处的切线相同.
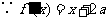 ,
,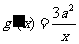 ,由题意
,由题意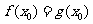 ,
,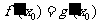 .
.
即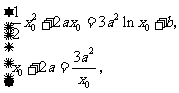 由
由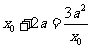 得:
得: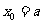 ,或
,或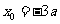 (舍去).
(舍去).
即有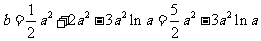 .
.
令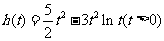 ,则
,则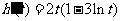 .于是当
.于是当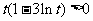 ,即
,即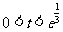 时,
时,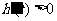 ;当
;当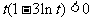 ,即
,即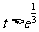 时,
时,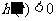 .故
.故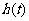 在
在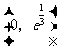 为增函数,
为增函数,
在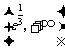 为减函数,∴
为减函数,∴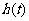 在
在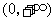 的最大值为
的最大值为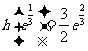 .
.
[巩固1] 设函数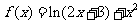 ,求
,求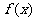 在区间
在区间 的最大值和最小值.
的最大值和最小值.
[巩固2] 已知函数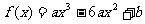 ,其图象为曲线C
,其图象为曲线C
(1) 直线l:y=x+1与曲线C相切于x轴上一点,求的a、b的值
(2)是否存在实数a、b,使f(x)在[-1、2]上取得最大值为3,最小值为-29。若存在,求出a、b的值,并指出函数y=f(x)的单调递增区间;若不存在,请说明理由。
2.“极值点”不是“点”,而是方程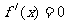 的根。
的根。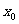 是函数
是函数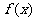 极值点则
极值点则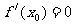 ;但是
;但是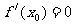 ,
,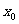 未必是极值点(还要求函数
未必是极值点(还要求函数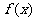 在
在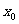 左右两侧的单调性相反);若
左右两侧的单调性相反);若
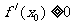 (或
(或 )恒成立,则函数
)恒成立,则函数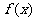 无极值。
无极值。
[举例1] 已知函数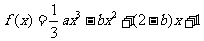 在
在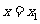 处取得极大值,在
处取得极大值,在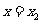 处取得极小值,且
处取得极小值,且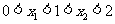 .(1)证明
.(1)证明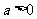 ;(2)若z=a+2b,求z的取值范围。
;(2)若z=a+2b,求z的取值范围。
解析:函数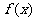 的导数
的导数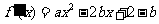 .
.
(Ⅰ)由函数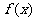 在
在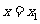 处取得极大值,在
处取得极大值,在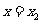 处取得极小值,知
处取得极小值,知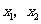 是
是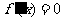 的两个根.所以
的两个根.所以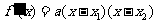 ;当
;当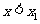 时,
时,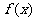 为增函数,
为增函数,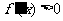 ,由
,由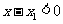 ,
,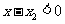 得
得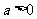 .
.
(Ⅱ)在题设下,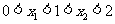 等价于
等价于 即
即 .
.
化简得 .此不等式组表示的区域为平面
.此不等式组表示的区域为平面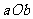 上三条直线:
上三条直线:
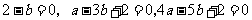 所围成的
所围成的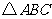 的内部,由“线性规划”的知识容易求得:
的内部,由“线性规划”的知识容易求得: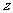 的取值范围为
的取值范围为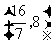 .
.
[举例2] 已知函数 在
在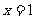 处有极值10,则
处有极值10,则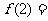
解析: 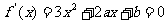 ,∴
,∴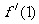 =
=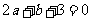 ①
①
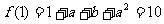 ② 由①②得:
② 由①②得: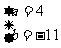 或
或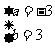
当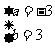 时,
时,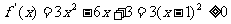 ,此时函数
,此时函数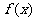 无极值,舍去;
无极值,舍去;
当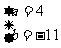 时
时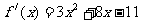 ,函数
,函数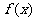 在
在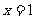 处左减右增,有极小值;
处左减右增,有极小值;
此时∴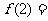 18 。注:在解决“已知函数的极值点求参变量”的问题时,为避免“增根”,需将求出的参变量的值代入
18 。注:在解决“已知函数的极值点求参变量”的问题时,为避免“增根”,需将求出的参变量的值代入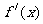 检验其是否为完全平方式,若是则函数无极值(单调),否则有极值;也可以对
检验其是否为完全平方式,若是则函数无极值(单调),否则有极值;也可以对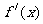 再次求导,看
再次求导,看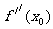 的值,为0则无极值,为正则有极小值,为负则有极大值。
的值,为0则无极值,为正则有极小值,为负则有极大值。
[巩固1]已知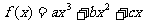 在区间[0,1]上是增函数,在区间
在区间[0,1]上是增函数,在区间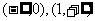 上是减函数,又
上是减函数,又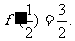 (Ⅰ)求
(Ⅰ)求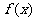 的解析式; (Ⅱ)若在区间
的解析式; (Ⅱ)若在区间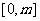 (m>0)上恒有
(m>0)上恒有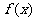 ≤x成立,求m的取值范围.
≤x成立,求m的取值范围.
[举例2]设函数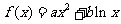 ,其中
,其中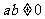 .证明:当
.证明:当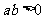 时,函数
时,函数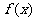 没有极值点;当
没有极值点;当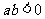 时,函数
时,函数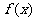 有且只有一个极值点,并求出极值.(07高考山东文21)
有且只有一个极值点,并求出极值.(07高考山东文21)
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com