3.(★★★★)如图1-5所示，水平轨道上停放着一辆质量为5.0×10² kg的小车A，在A的右方L=8.0 m处，另一辆小车B正以速度v_B=4.0 m/s的速度向右做匀速直线运动远离A车，为使A车能经过t=10.0 s时间追上B车，立即给A车适当施加向右的水平推力使小车做匀变速直线运动，设小车A受到水平轨道的阻力是车重的0.1倍，试问：在此追及过程中，推力至少需要做多少功？　　　 取g=10 m/s²)

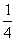　　 4.(★★★★)如图1-6所示，在光滑的水平面上放置一质量为m的小车，小车上有一半径为R的光滑的弧形轨道，设有一质量为m的小球，以v₀的速度，方向水平向左沿圆弧轨道向上滑动，达到某一高度h后，又沿轨道下滑，试求h的大小及小球刚离开轨道时的速度.

2.(★★★★)两辆完全相同的汽车，沿水平直路一前一后匀速行驶，速度均为v₀,若前车突然以恒定的加速度刹车，在它刚停住时，后车以前车刹车时的加速度开始刹车，已知前车在刹车过程中所行驶的距离为s,若要保证两车在上述情况中不相撞，则两车在匀速行驶时保持距离至少应为多少？

由示意图找两

解决“追碰”问题大致分两类方法，即数学法(如函数极值法、图象法等)和物理方法(参照物变换法、守恒法等).

●歼灭难点训练

1.(★★★★)凸透镜的焦距为f,一个在透镜光轴上的物体，从距透镜3f处，沿光轴逐渐移动到距离2f处，在此过程中

A.像不断变大　　　　

B.像和物之间距离不断减小

C.像和焦点的距离不断增大　

D.像和透镜的距离不断减小

2.“碰撞”问题

碰撞过程作用时间短，相互作用力大的特点，决定了所有碰撞问题均遵守动量守恒定律.对正碰，根据碰撞前后系统的动能是否变化，又分为弹性碰撞和非弹性碰撞.

弹性碰撞：系统的动量和动能均守恒，因而有：

m₁v₁+m₂v₂=m₁v₁′+m₂v₂′　　　　　　　　　　　　　　　　　　　　　　　　　 ①

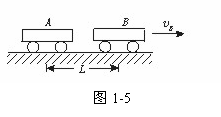
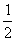m₁v₁²+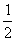m₂v₂²=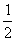m₁v₁′²+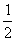m₂v₂′² ②

上式中v₁、v₁′分别是m₁碰前和碰后的速度，v₂、v₂′分别是m₂碰前和碰后的速度.

解①②式得

v₁′=　　　　　　　　　　　　　　　　　 ③

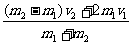v₂′=　　　　　　　　　　　　　　 ④

完全非弹性碰撞：m₁与m₂碰后速度相同，设为v,则

m₁v₁+m₂v₂=(m₁+m₂)v,v=.

系统损失的最大动能ΔE_km=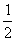m₁v₁²+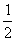m₂v₂²- 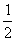(m₁+m₂)v².非弹性碰撞损失的动能介于弹性碰撞和完全非弹性碰撞之间.

在处理碰撞问题时，通常要抓住三项基本原则：

(1)碰撞过程中动量守恒原则.

(2)碰撞后系统动能不增原则.

(3)碰撞后运动状态的合理性原则.

碰撞过程的发生应遵循客观实际.如甲物追乙物并发生碰撞，碰前甲的速度必须大于乙的速度，碰后甲的速度必须小于、等于乙的速度或甲反向运动.

1.“追及”问题

讨论追及、相遇的问题，其实质就是分析讨论两物体在相同时间内能否到达相同的空间位置问题.一定要抓住两个关系：即时间关系和位移关系.一个条件：即两者速度相等，它往往是物体间能否追上、追不上或(两者)距离最大、最小的临界条件，也是分析判断的切入点.

“追碰”问题，包括单纯的“追及”类、“碰撞”类和“追及碰撞”类，处理该类问题，首先要求学生有正确的时间和空间观念(物体的运动过程总与时间的延续和空间位置的变化相对应).同时，要求考生必须理解掌握物体的运动性质及规律，具有较强的综合素质和能力.该类问题综合性强，思维容量大，且与生活实际联系密切，是高考选拔性考试不可或缺的命题素材，应引起广泛的关注.

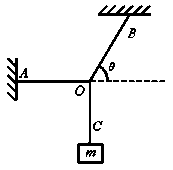
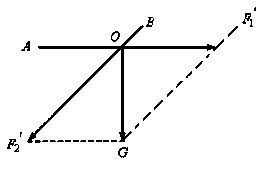
41. 如图所示重物的质量为m，轻细绳AO和BO的A、B端是固定的，静止时AO是水平的，BO与水平面夹角为θ，AO的拉力F₁和BO的拉力F₂的大小是：(全国)

　 A.F₁＝mgcosθ　 B.F₁＝gcotθ　 C.F₂＝mgsinθ　 D.F₂＝mg/sinθ

[解析]

[答案]B、D

40. 如图所示，用一个水平外力F将木块压紧在竖直墙上，保持静止不动，当水平外力F增大时，木块与墙之间的摩擦力　　，最大静摩擦力　　。(填增大，不变，减小)

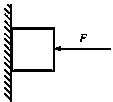
[解析]

[答案]不变；增大

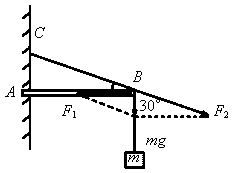
39. 水平横梁的一端A插在墙壁内，另一端装有一个小滑轮B。一轻绳的一端C固定于墙壁上，另一端跨过滑轮后悬挂一质量为m＝10kg的重物，∠CBA＝30°，如图所示。则滑轮受到绳子的作用力为：(g取10m/s²)(上海)

　 A.50N 　　B.50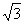N 　　C.100N 　　D.100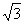N

　　 [解析]

[答案]D

38. 如图所示，均匀杆被细绳拉住而静止，试画出杆所受的弹力。

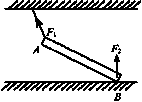
　　 [解析]