108.质量都是M的甲、乙两小车都静止在光滑水平地面上，甲车上站着一个质量为m的人，现在人以相对于地面的速度v从甲车跳上乙车，接着以同样大小的相对于地的速度反向跳回甲车，最后两车速度大小分别为v_甲、v_乙，则下列说法中正确的是(　 )

A．v_甲∶v_乙 = (M + m)∶M

B．v_甲∶v_乙 = M∶(M + m)

C．人对甲车做的功W₁大于人对乙车的功W₂

D．人对甲车做的功W₁小于人对乙车的功W₂

4. 动量守恒定律的应用

⑴应用动量守恒定律时应注意：①条件性；②整体性；③矢量性；④相对性；⑤同时性．

⑵碰撞：两个物体在极短时间内发生相互作用，这种情况称为碰撞。由于作用时间极短，一般都满足内力远大于外力，所以可以认为系统的动量守恒。碰撞又分弹性碰撞、非弹性碰撞、完全非弹性碰撞三种。

　　　 a.完全弹性碰撞：没有动能损失。

质量为m1速度为v1的物体A去碰质量为m 2静止的物体B，碰后A、B的最终速度分别为：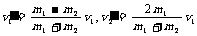

　　 b.完全非弹性碰撞：碰后系统有共同速度，系统的动能损失最大。

　　 c.非完全弹性碰撞：介于弹性碰撞和完全非弹性碰撞之间 ，有动能损失。

此类碰撞问题要考虑三个因素：①碰撞中系统动量守恒；②碰撞过程中系统动能不增加；③碰前、碰后两个物体的位置关系(不穿越)和速度大小应保证其顺序合理。

3.动量守恒定律的表达形式

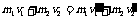
Δp₁+Δp₂=0，Δp₁= - Δp₂

2.动量守恒定律成立的条件：⑴系统不受外力或者所受外力之和为零；⑵系统受外力，但外力远小于内力，可以忽略不计；⑶系统在某一个方向上所受的合外力为零，则该方向上动量守恒。

1.动量守恒定律：一个系统不受外力或者受外力之和为零，这个系统的总动量保持不变。

107.通过估算来说明鸟类对飞机的威胁。设鸟的质量为 1kg，飞机的飞行速度为500m/s ，则鸟与飞机相撞时，冲击力约为　　　　　　　 N。

考点26．动量守恒定律

106.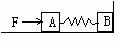质量都是1千克的物体A、B中间用一轻弹簧连接，放在光滑的水平地面上。现在使B物体靠在墙上，用力推物体A压缩弹簧。这个过程中外力做功8 J ，待系统静止后突然撤除外力。从突然撤除外力到弹簧恢复原长的过程中墙对B物体的冲量大小是　　　 　N·S 。当A、B间距最大时，B物体的速度大小为　　　　 m/ s ，这时弹簧具有的弹性势能为　　　　　 。

105.美国著名的网球运动员罗迪克的发球时速最快可达214.35km/h，这也是最新的网球发球时速的世界记录，若将罗迪克的发球过程看作网球在球拍作用下沿水平方向的匀加速直线运动，质量为57.5g的网球从静止开始经0.5m的水平位移后速度增加到214.35km/h，则在上述过程中，网球拍对网球的作用力大小为　 (　　 )

A．154N　　 B．208N　　 C．556N　　 D．1225N

104.撑杆跳高运动员的质量为m，他越过横杆后几乎是竖直落下，刚接触垫子时的速度大小为v₁，反弹离开垫子时的速度大小不为v₂。则垫子对他的冲量大小(　　 )

A 等于mv₁+mv₂　　　　　　　　 B等于mv₁-mv₂

C小于mv₁-mv₂ D大于mv₁+mv₂

103.完全相同的甲、乙两只小船，都停在平静的水面上，甲船载有一个人，乙船是空的。现在人从甲船跳到乙船，若不计阻力，则两船相比(　　 )

A.两船受到的人的冲量一样大　　　　　　　 B.两船将有相同的速率

C.甲船比乙船受到的人的冲量大　　　　　　 D.人和船的质量未知，无法比较两船的运动速率