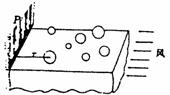
141.如图所示，桌面上有许多大小不同的塑料球，它们的密度均为ρ，有水平向左恒定的风作用在球上，使它们做匀加速运动(摩擦不计)，已知风对球的作用力与球的最大截面成正比，即F=kS(k为一常量)。

⑴对塑料球来说，空间存在一个风力场，请定义风力场强度。

⑵在该风力场中风力对球做功与路径无关，可引入风力势能的概念，若以栅栏P为参考平面，写出风力势能E_P的表达式。

⑶写出风力场中机械能守恒定律的表达式。(球半径用r表示，第一状态速度为v₁，位置为x₁；第二状态速度为v₂，位置为x₂)

考点32．动量知识与机械能知识的应用(包括碰撞、反冲、火箭)

140.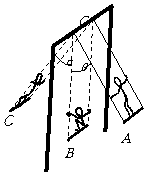如图是打秋千的示意图。最初人直立站在踏板上(A点所示)，绳与竖直方向成θ角，人的重心到悬点O的距离为L₁；从A点向最低点B运动过程中，人由直立状态自然下蹲，在B点人的重心到悬点O的距离为L₂；在最低点处，人突然由下蹲状态变成直立状态(人的重心到悬点O的距离恢复为L₁)且保持该状态到最高点C.设人的质量为m，踏板和绳的质量不计，空气阻力不计.求：

①人刚到最低点B还处于下蹲状态时，两根绳中的总拉力F为多大？

②人到达左端最高点C时，绳与竖直方向的夹角α为多大？(用反三角函数表示)

139.如图所示， 一条质量不计的细线一端拴一个质量为M的砝码，另一端系一个质量为m的圆环，将圆环套在一根光滑的竖直杆上．滑轮与竖直杆相距0.3m，环与滑轮在同一水平位置，由静止开始释放，环向下滑的最大距离是0.4m，不计摩擦力．问(1)M∶m=？(2)圆环下滑0.3m时速度多大？

3.机械能守恒的应用：应用守恒定律来研究物理问题时，可以只考虑过程的初始状态和终了状态，而不必考虑两个状态之间过程的细节，可以简化研究过程，这正是守恒定律的特点和优点。

2.机械能守恒定律的数学形式：E_K1+E_P1＝E_K2+E_P2 ； E₁＝E₂ ；ΔE_P+ΔE_K＝0

2.机械能守恒条件的条件：①系统只受重力和弹簧弹力；②系统除受重力和弹簧弹力外，还受到其它力的作用，但这些力不做功；③系统除受重力和弹簧弹力外，还受到其它力的作用，这些力做功，但对系统做功的代数和为零。

1.机械能守恒：在只有重力和弹簧弹力做功的情形下，物体的动能和重力势能可以相互转化，但机械能的总量保持不变。

138.如图所示，一轻质弹簧两端连着物体A和B，放在光滑的水平面上，物体A被水平速度为V₀ 的子弹射中并嵌在其中。已知物体A的质量是物体B质量的3/ 4，子弹的质量是物体B的质量的1/4，求弹簧压缩到最短时B的速度及弹簧具有的最大弹性势能。

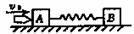
考点31．机械能守恒定律及其应用

137.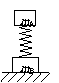如图所示，A、B两物体的质量分别为m_A、m_B，用劲度为k的轻弹簧相连，开始时，A、B都处于静止状态。现对A施加一个竖直向上的力F，缓慢将A提起，直到使B恰好对地面没有压力。这时撤去力F，A由静止向下运动到具有最大速度为止，重力对A做的功是(　　　 )

A.m_A²g²/k　　　 B.m_B²g²/k　　 C.m_A (m_A +m_B)g²/k　　 D.m_B (m_A +m_B)g²/k

考点30．弹性势能

弹性势能的大小与弹性形变有关，一般来说，弹性形变量越大，所具有的弹性势能就越多。

3.重力做功与重力势能变化关系

W_G＝－ΔE_P＝E_P1－E_P2

重力做正功，重力势能减小；重力做负功，重力势能增加。