
1.考察下列一组不等式: 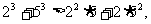

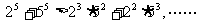 .将上述不等式在左右两端仍为两项和的情况下加以推广,使以上的不等式成为推广不等式的特例,则推广的不等式可以是
.
.将上述不等式在左右两端仍为两项和的情况下加以推广,使以上的不等式成为推广不等式的特例,则推广的不等式可以是
.
2. 间接证明:间接证明是不同于直接证明的又一类证明方法,反证法是一种常用的间接证明方法;反证法即从
开始,经过正确的推理,说明假设错误,从而证明了原命题成立,这样的证明方法叫做反证法(归谬法).
间接证明:间接证明是不同于直接证明的又一类证明方法,反证法是一种常用的间接证明方法;反证法即从
开始,经过正确的推理,说明假设错误,从而证明了原命题成立,这样的证明方法叫做反证法(归谬法).
|
例1.若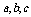 均为实数,且
均为实数,且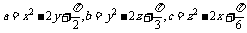 。
。
求证: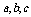 中至少有一个大于0。
中至少有一个大于0。
答案:(用反证法)
假设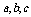 都不大于0,即
都不大于0,即 ,则有
,则有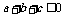 ,
,
而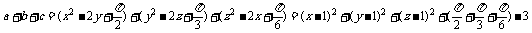 =
=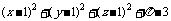
∴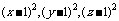 均大于或等于0,
均大于或等于0,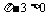 ,∴
,∴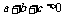 ,这与假设
,这与假设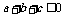 矛盾,故
矛盾,故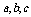 中至少有一个大于0。
中至少有一个大于0。
变式训练1:用反证法证明命题“ 可以被5整除,那么
可以被5整除,那么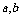 中至少有一个能被5整除。”那么假设的内容是
中至少有一个能被5整除。”那么假设的内容是
答案:a,b中没有一个能被5整除。解析:“至少有n个”的否定是“最多有n-1个”。
例2. △ABC的三个内角A、B、C成等差数列,
求证: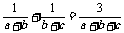 。
。
答案:证明:要证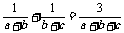 ,即需证
,即需证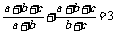 。
。
即证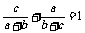 。
。
又需证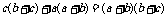 ,需证
,需证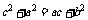
∵△ABC三个内角A、B、C成等差数列。∴B=60°。
由余弦定理,有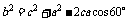 ,即
,即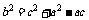 。
。
∴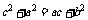 成立,命题得证。
成立,命题得证。
变式训练2:用分析法证明:若a>0,则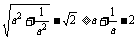 。
。
答案:证明:要证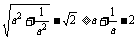 ,
,
只需证 。
。
∵a>0,∴两边均大于零,因此只需证
只需证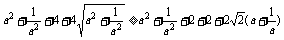 ,
,
只需证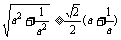 ,只需证
,只需证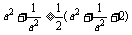 ,
,
即证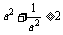 ,它显然成立。∴原不等式成立。
,它显然成立。∴原不等式成立。
例3.已知数列 ,
,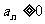 ,
,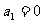 ,
,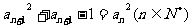 .
.
记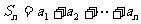 .
.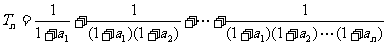 .
.
求证:当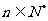 时,
时,
(1)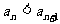 ;
;
(2) ;
;
(3) 。
。
解:(1)证明:用数学归纳法证明.
①当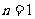 时,因为
时,因为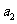 是方程
是方程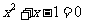 的正根,所以
的正根,所以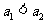 .
.
②假设当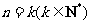 时,
时,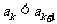 ,
,
因为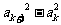
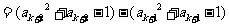
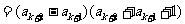 ,
,
所以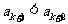 .
.
即当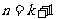 时,
时,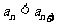 也成立.
也成立.
根据①和②,可知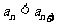 对任何
对任何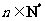 都成立.
都成立.
(2)证明:由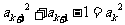 ,
,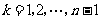 (
(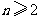 ),
),
得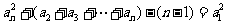 .
.
因为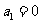 ,所以
,所以 .
.
由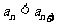 及
及 得
得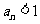 ,
,
所以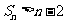 .
.
(3)证明:由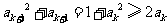 ,得
,得
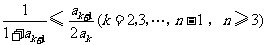
所以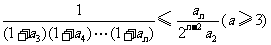 ,
,
于是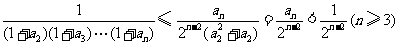 ,
,
故当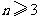 时,
时,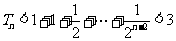 ,
,
又因为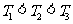 ,
,
所以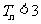 .
.
推理与证明章节测试题
1.直接证明:直接从原命题的条件逐步推得结论成立,这种证明方法叫直接证明;
直接证明的两种基本方法--分析法和综合法
⑴ 综合法 -- ;⑵分析法 -- ;
4.合情推理是根据已有的事实和正确的结论(包括定义、公理、定理等)、实验和实践的结果,以及个人的经验和直觉等推测某些结果的推理过程,归纳和类比是合情推理常用的思维方法;在解决问题的过程中,合情推理具有猜测和发现结论、探索和提供思路的作用,有得于创新意识的培养。演绎推理是根据已有的事实和正确的结论,按照严格的逻辑法则得到的新结论的推理过程.
|
例1. 已知: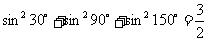 ;
;
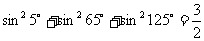
通过观察上述两等式的规律,请你写出一般性的命题:
________________________________________=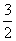 ( * )并给出( * )式的证明.
( * )并给出( * )式的证明.
解:一般形式: 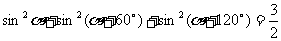
证明:左边 = 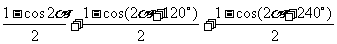
= 
= 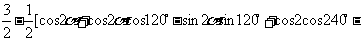
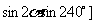
= 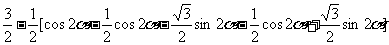 =
=
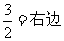
(将一般形式写成 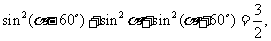
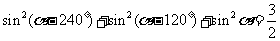 等均正确。)
等均正确。)
变式训练1:设 ,
,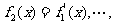
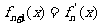 ,n∈N,则
,n∈N,则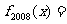
解: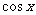 ,由归纳推理可知其周期是4
,由归纳推理可知其周期是4
例2. 在平面上,我们如果用一条直线去截正方形的一个角,那么截下的一个直角三角形,
按图所标边长,由勾股定理有:
 设想正方形换成正方体,把截线换成如图的截面,这时从正方体上截下三条侧棱两两垂直的三棱锥O-LMN,如果用
设想正方形换成正方体,把截线换成如图的截面,这时从正方体上截下三条侧棱两两垂直的三棱锥O-LMN,如果用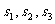 表示三个侧面面积,
表示三个侧面面积,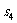 表示截面面积,那么你类比得到的结论是
.
表示截面面积,那么你类比得到的结论是
.
解: 。
。
变式训练2:在△ABC中,若∠C=90°,AC=b,BC=a,则△ABC的外接圆的半径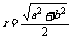 ,把上面的结论推广到空间,写出相类似的结论。
,把上面的结论推广到空间,写出相类似的结论。
答案:本题是“由平面向空间类比”。考虑到平面中的图形是一个直角三角形,
所以在空间中我们可以选取有3个面两两垂直的四面体来考虑。
取空间中有三条侧棱两两垂直的四面体A-BCD,且AB=a,AC=b,AD=c,
则此三棱锥的外接球的半径是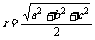 。
。
例3. 请你把不等式“若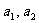 是正实数,则有
是正实数,则有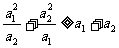 ”推广到一般情形,并证明你的结论。
”推广到一般情形,并证明你的结论。
答案: 推广的结论:若 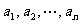 都是正数,
都是正数,

证明: ∵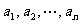 都是正数 ∴
都是正数 ∴ 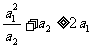 ,
,
………,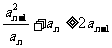 ,
,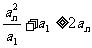

变式训练3:观察式子: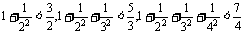 ,…,则可归纳出式子为( )
,…,则可归纳出式子为( )
A、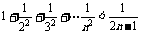 B、
B、
C、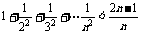 D、
D、
答案:C。解析:用n=2代入选项判断。
例4. 有一段演绎推理是这样的:“直线平行于平面,则平行于平面内所有直线;已知直线
 平面
平面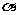 ,直线
,直线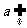 平面
平面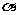 ,直线
,直线 ∥平面
∥平面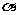 ,则直线
,则直线 ∥直线
∥直线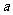 ”的结论显然是错误的,这是因为
( )
”的结论显然是错误的,这是因为
( )
A.大前提错误 B.小前提错误 C.推理形式错误 D.非以上错误
答案:A。解析:直线平行于平面,并不平行于平面内所有直线。
变式训练4:“ AC,BD是菱形ABCD的对角线,
AC,BD是菱形ABCD的对角线,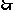 AC,BD互相垂直且平分。”补充以上推理的大前提是
。
AC,BD互相垂直且平分。”补充以上推理的大前提是
。
答案:菱形对角线互相垂直且平分
|
3.演绎推理:演绎推理是 ,按照严格的逻辑法则得到的 推理过程;三段论常用格式为:①M是P,② ,③S是P;其中①是 ,它提供了一个个一般性原理;②是 ,它指出了一个个特殊对象;③是 ,它根据一般原理,对特殊情况作出的判断.
2.合情推理包括 和 ;
归纳推理:从个别事实中推演出 ,这样的推理通常称为归纳推理;归纳推理的思维过程是: 、 、 .
类比推理:根据两个(或两类)对象之间在某些方面的相似或相同,推演出它们在其它方面也 或 ,这样的推理称为类比推理,类比推理的思维过程是: 、 、 .
1. 推理一般包括合情推理和演绎推理;
2.推理与证明与数列、几何、等有关内容综合在一起的综合试题多。
第1课时 合情推理与演绎推理
|
了解数学归纳法的原理,能用数学归纳法证明一些简单的数学命题.
|
1.推理与证明的内容是高考的新增内容,主要以选择填空的形式出现。
2.了解间接证明的一种基本方法──反证法;了解反证法的思考过程、特点。
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com