
1.判断下列函数的奇偶性:
(1) ; (2)
; (2)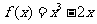
(3)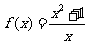 ; (4)
; (4)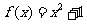 .
.
1.3.2单调性与最大(小)值
练习(第36页)
5.最小值.
5.设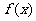 是定义在区间
是定义在区间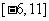 上的函数.如果
上的函数.如果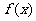 在区间
在区间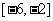 上递减,在区间
上递减,在区间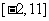 上递增,画出
上递增,画出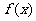 的一个大致的图象,从图象上可以发现
的一个大致的图象,从图象上可以发现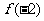 是函数
是函数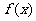 的一个
.
的一个
.
4.证明:设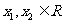 ,且
,且 ,
,
因为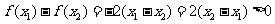 ,
,
即 ,
,
所以函数 在
在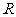 上是减函数.
上是减函数.
4.证明函数 在
在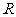 上是减函数.
上是减函数.
3.解:该函数在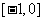 上是减函数,在
上是减函数,在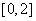 上是增函数,在
上是增函数,在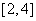 上是减函数,
上是减函数,
在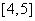 上是增函数.
上是增函数.
3.根据下图说出函数的单调区间,以及在每一单调区间上,函数是增函数还是减函数.
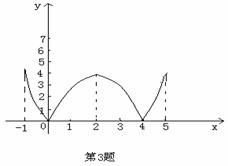
2.解:图象如下
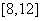 是递增区间,
是递增区间,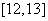 是递减区间,
是递减区间,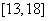 是递增区间,
是递增区间,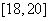 是递减区间.
是递减区间.
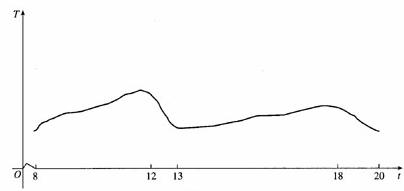
2.整个上午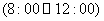 天气越来越暖,中午时分
天气越来越暖,中午时分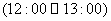 一场暴风雨使天气骤然凉爽了许多.暴风雨过后,天气转暖,直到太阳落山
一场暴风雨使天气骤然凉爽了许多.暴风雨过后,天气转暖,直到太阳落山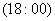 才又开始转凉.画出这一天
才又开始转凉.画出这一天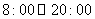 期间气温作为时间函数的一个可能的图象,并说出所画函数的单调区间.
期间气温作为时间函数的一个可能的图象,并说出所画函数的单调区间.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com