
22.( 12分)设函数
12分)设函数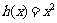 ,
, (
(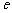 为自然对数的底).
为自然对数的底).
⑴ 求函数 的极值;
的极值;
⑵ 若存在常数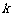 和
和 ,使得函数
,使得函数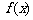 和
和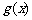 对其定义域内的任意实数
对其定义域内的任意实数 分别满足
分别满足
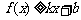 和
和 ,则称直线
,则称直线 :
: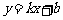 为函
为函 数
数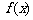 和
和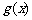 的“隔
的“隔
离直线”.试问: 函数
函数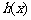 和
和 是否存在“隔离直线”?若存在,求出“隔
是否存在“隔离直线”?若存在,求出“隔
离直线”方程;若不存在,请说明理由.
2010届第三次四校联考
⒘(10分)已知向量 ,
, ,设函
,设函 数
数
 ,若角
,若角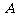 是锐角三角形的最大内角,求
是锐角三角形的最大内角,求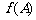 的取值范围.
的取值范围.
⒙(12分)将编号为1,2,3,4,5的五个相同小球,随机放入编码分别为1,2,3,
4,5的五个小盒中,每盒仅放一球,若第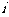 号小球恰好落入第
号小球恰好落入第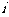 号小盒中,则称其
号小盒中,则称其
为一个匹对,用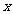 表示匹对的个数.
表示匹对的个数.
⑴ 求 号小球不落入
号小球不落入 号盒子中,且
号盒子中,且 号小球不落入
号小球不落入 号盒子中的概率;
号盒子中的概率;
⑵ 求匹对数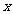 的分布列和数学期望.
的分布列和数学期望.
⒚(12分)如图,四棱锥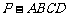 中,底面
中,底面 是直角梯形,
是直角梯形, ,
,
 ,
, ,侧面
,侧面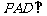 底面
底面 ,且
,且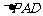 为等腰直角三角形,
为等腰直角三角形,

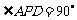 ,
,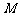 为
为
 的中点.
的中点.
⑴ 求证: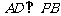 ;
;
⑵ 求二面角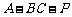 的大小.
的大小.
⒛(12分)已知数列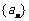 的首项为
的首项为 ,前
,前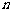 项和为
项和为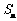 ,且对任意的
,且对任意的 ,当
,当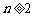
时,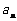 总是
总是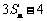 与
与 的等差中项.
的等差中项.
⑴ 求数列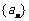 的通项公式;
的通项公式;
⑵ 设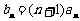 ,
, 是数列
是数列 的前
的前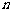 项和,
项和, ,求
,求 .
.
21.(12分)曲线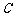 是中心在原点,焦点在
是中心在原点,焦点在 轴上的双曲线,已知它的一个焦点
轴上的双曲线,已知它的一个焦点 的
的
坐标为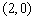 ,一条渐近线的方程为
,一条渐近线的方程为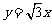 ,过焦点
,过焦点 作直线交曲线
作直线交曲线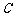 的右支于
的右支于
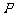 、
、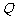 两点,
两点,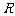 是弦
是弦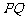 的中点.
的中点.
⑴ 求曲线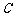 的方程;
的方程;
⑵ 若在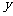 轴左侧能作出直线
轴左侧能作出直线 :
: ,使以线段
,使以线段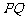 为直径的圆与直线
为直径的圆与直线 相切,
相切,
求实数 的取值范围.
的取值范围.
⒔ 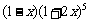 展开式按
展开式按 的升幂排列,则第3项的系数为 .
的升幂排列,则第3项的系数为 .
⒕  、
、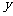 满足约束条件:
满足约束条件: ,则
,则 的最小值是 .
的最小值是 .
⒖ 已知两点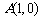
 ,
,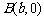 ,若抛物线
,若抛物线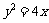 上存在点
上存在点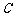 使
使 为等边三角形,
为等边三角形,
则 .
.
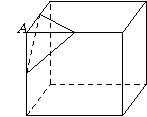 ⒗ 如图,设
⒗ 如图,设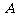 是棱长为
是棱长为 的正方体的一个顶点,过从此顶
的正方体的一个顶点,过从此顶
点出发的三条棱的中点作截面,对正方体的所有顶点都
如此操作,所得的各截面与正方体各面共同围成一个多
面体,则关于此多面体有以下结论:①
有 个顶点;
个顶点;
②
有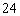 条棱;③
有
条棱;③
有
 个面;④
表面积为
个面;④
表面积为 ;⑤
体
;⑤
体
积为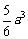 .其中正确的结论是 (要求填上所有正
.其中正确的结论是 (要求填上所有正
确结论的序号).
⒈ 在复平面内,复数 所对应的点位于
所对应的点位于
A.第一象限 B.第二象限 C.第三象限 D.第四象限
⒉ 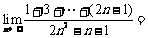
A. B.
B. C.
C. D.
D.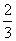
⒊ 在等差数列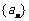 中,有
中,有 ,则此数列的前
,则此数列的前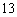 项和为
项和为
A.24
B.39 C.52
 D.104
D.104
⒋ 若曲线 在点
在点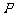 处的切线平行于直线
处的切线平行于直线 ,则点
,则点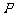 的坐标为
的坐标为
A.(1,3) B.(-1,3) C.(1,0) D.(-1,0)
⒌ 设偶函数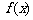 在
在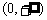 上为减函数,且
上为减函数,且 ,则不等式
,则不等式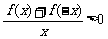 的
的
解集为
A. B.
B.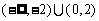 C.
C.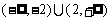 D.
D.
⒍ 设集合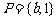 ,
,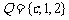 ,
, ,若
,若 、
、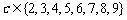 ,则
,则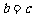 的
的
概率是
A.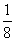 B.
B.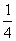 C.
C. D.
D.
⒎ 已知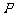 是边长为2的正
是边长为2的正 边
边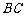 上的动点,则
上的动点,则 的值
的值
A.最大值为8 B.是定值6 C.最小值2 D.与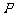 的位置有关
的位置有关
⒏ 将函数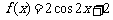 的图象按向量
的图象按向量 平移后得
平移后得 到的图象的函数为Z#X#X#K]
到的图象的函数为Z#X#X#K]
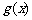 ,若函数
,若函数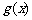 是奇函数,且在
是奇函数,且在 上是增函数,则
上是增函数,则 的一个值为
的一个值为
A.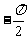 B.
B. C.
C.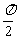 D.
D.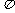
⒐ 已知四棱柱 的底面为正方形,侧棱与底面边长相等,且点
的底面为正方形,侧棱与底面边长相等,且点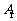 在底
在底
面 内的射影为正方形
内的射影为正方形 的中心,则
的中心,则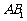 与底面
与底面 所成角的正弦值
所成角的正弦值
等于
A.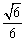 B.
B. C.
C. D.
D.
⒑ 已知函数 ,若
,若 有解,则实数
有解,则实数 的取值范围是
的取值范围是
A.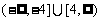 B.
B. C.
C. D.
D.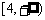
⒒ 将正方体 的各面涂色,任何相邻两个面不同色,现在有5种不同
的各面涂色,任何相邻两个面不同色,现在有5种不同
的颜色,并且涂好了过顶点 的3个面的颜色,那么其余的3个面的涂色方案共有
的3个面的颜色,那么其余的3个面的涂色方案共有
A.15种  B.14种
C.13种
D.12种
B.14种
C.13种
D.12种
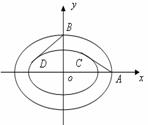 ⒓ 北京奥运会主体育场“鸟巢”的钢结构俯视图如图所示,
⒓ 北京奥运会主体育场“鸟巢”的钢结构俯视图如图所示,
内外两圈的钢骨架是离心率相同的椭圆,外层椭圆顶点
向内层椭圆引切线 、
、 ,设内层椭圆方程为
,设内层椭圆方程为
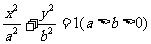 ,则外层椭圆
,则外层椭圆 方程可设为
方程可设为
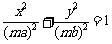
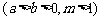 .若
.若 与
与 的斜
的斜
率之积为 ,则椭圆的离心率为
,则椭圆的离心率为
A.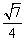 B.
B.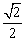 C.
C.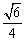 D.
D.
20.成都地铁是成都市的城市轨道交通系统,于 2005 年 12 月正式开工建设,预计 20 10 年 10 月地铁 1 号线一期工程建成通车。成都是中国西部第一座开工建设地铁的城市。请你为成都地铁的开通写一条宣传语.要求主题鲜明,构思新颖,语言简明,富有文采,必须原创。( 5 分)
答:
19.把下列语句填人文中横线处,使上下文语意连贯。(只填序号) ( 5 分)


由语言和意象的研究再进一步就是意境和风格的研究。 _______________________
① 意境研究是中国诗歌艺术研究的一个重要环节
② 词语的组合构成诗篇,意象的组合构成意境,境生于象而超乎象
③ 风格研究需深人到人格的领域,对诗人作出总体把握
④ 揭示意境的形成,既可看到诗人的构思过程,又可窥察读者的鉴赏心理
⑤ 诗歌艺术研究的最高层次就是风格研究
⑥ 诗歌的意境和诗人的风格也有密切的关系
18.用一句话概括下面新闻的主要内容。(不超过 24 字, 5 分)
据北京 1 月 25 日电环保部部长周生贤今天透露,截至 2009 年年底,我国“十一五”规划中确定的二氧化硫的减排任务已提前一年完成,另一个考核指标-- 化学需氧量也完成了消减任务量的 96 . 6 % ,今年实现减排目标毫无悬念。
“十一五”规划中的环保任务是,到 2010 年,我国的主要污染物二氧化硫、化学需氧量要比 2005 年消减 10 %。从过去几年公布的数字看,“十一五”的第一年,即 2006 年,全国绝大部分地区都没有完成减排任务。当时环保部门曾发出警告:如果地方政府还不把减排当回事儿,那么,“十一五”末期,我们仍会面临环保任务完不成的尴尬。事情在 2007 年发生了变化。这一年,全国污染物排放总量首次出现了下降的势头。这个时点在环保系统内被称为“减排的拐点”。此前我国确立的“五年”规划污染减排目标都没有实现。
13.按要求写出名篇名句中的空缺部分。(两题任选一题) ( 5 分)
( l ) ,身死人手,为天下笑者,何也?(贾谊 《 过秦论 》 )
陶渊明深深地认识到,过去的已经无法再来,但未来可以由自己把握。在 《 归去来兮辞 》 中,表现这一思想的诗句是_____________________,______________ 。
《 迢迢牵牛星 》 中描写织女劳作的诗句是 , 。
(2)方正之不容也,___________________________。(司马迁 《 屈原列传 》 )
苏轼在 《 赤壁赋 》 中“ _,_________ ” 两句表达了自己对人生短暂的悲叹和对自然永恒的羡慕。
秦观在 《 鹊桥仙 》 中表现牛郎织女美好爱情的句子是_______________,_________ 。
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com