
9、解:1)设两抛物线的交点为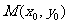 ,则
,则
由题意得: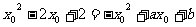
即: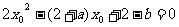 ①
①
又由导数可得: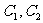 在点
在点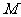 处的切线斜率为:
处的切线斜率为:
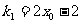 ,
, 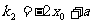
由已知: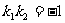 ,即:
,即: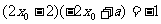
即: ②
②
联立①②,消去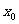 ,得
,得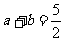 。
。
2)由1)可知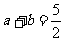 ,又
,又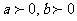
∴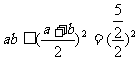 =
=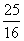 ,当且仅当
,当且仅当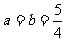 时取等号,
时取等号,
∴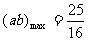 。
。
8、解:由已知,抛物线过点(1,1),(2,-1)
∴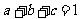
 ①
① 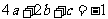 ②
②
又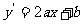 ∴由
∴由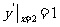 得:
得: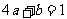 ③
③
∴由①②③联立方程组解得: 。
。
6、 7、0.32;36;0.08
7、0.32;36;0.08
例1、解:(1)频率分布表
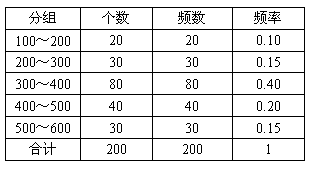
(2)频率分布直方图
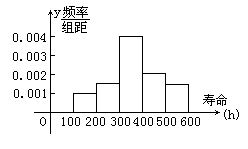
(3)由频率分布直方图,可知寿命在100-400h内的概率为0.65。
(4)由频率分布直方图可知,寿命在400h以上的概率为0.20+0.15=0.35
(或1-0.65=0.35)
(5)样本的期望值为


因此,估计总体生产的电子元件寿命的期望值为365h。
例2、解:1)∵ ∴
∴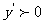
∴函数在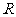 上递增,且函数无极值。
上递增,且函数无极值。
2)由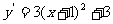 知:当
知:当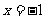 时,
时,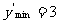 ,
,
把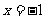 代入原方程,得
代入原方程,得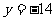 ,
,
∴当点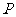 坐标为
坐标为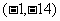 时,切线的斜率最小值为3,
时,切线的斜率最小值为3,
∴切线的方程为: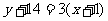 即:
即: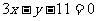
例3、 解:∵直线y=kx过原点,又点(x0,y0)在直线l上,
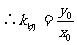
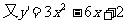
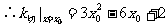
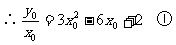
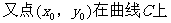
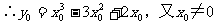
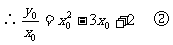
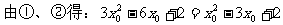

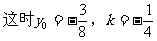
冲刺强化训练(6)
1、A; 2、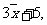
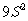 ; 3、C; 4、B; 5、A;
; 3、C; 4、B; 5、A;
9. 设抛物线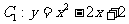 与抛物线
与抛物线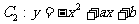 在它们的一个交点处的切线互相垂直。
在它们的一个交点处的切线互相垂直。
1) 求 、
、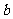 之间的关系;
之间的关系;
2) 若 >0,
>0,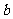 >0,求
>0,求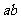 的最大值。
的最大值。
第6讲 统计、导数
8. 已知抛物线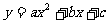 通过点
通过点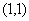 ,且在
,且在 处的切线的斜率为1,求
处的切线的斜率为1,求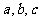 的值。
的值。
7. 如图是容量为100的样本的频率分布直方图,试根据图形中的数据填空
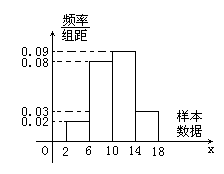
(1)样本数据落在范围[6,10)内的频率为_____________。
(2)样本数据落在范围[10,14)内的频数为_____________。
(3)总体在范围[2,6]内的概率约为_____________。
6. 过曲线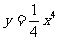 上一点,倾斜角为
上一点,倾斜角为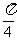 的切线方程是_____________。
的切线方程是_____________。
5. 函数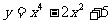 的单调递减区间为 ( )
的单调递减区间为 ( )
A.  及(0,1)
B.
及(0,1)
B. 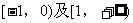
C. 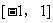 D.
D.
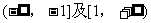
4. 过抛物线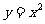 上的点M(
上的点M(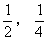 )的切线的倾斜角是 ( )
)的切线的倾斜角是 ( )
A. 30° B. 45° C. 60° D. 90°
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com