
3.设平面内有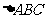 ,且
,且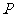 表示这个平面内的动点,指出属于集合
表示这个平面内的动点,指出属于集合
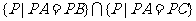 的点是什么.
的点是什么.
2.解:(1)由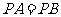 ,得点
,得点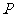 到线段
到线段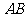 的两个端点的距离相等,
的两个端点的距离相等,
即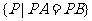 表示的点组成线段
表示的点组成线段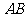 的垂直平分线;
的垂直平分线;
(2)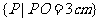 表示的点组成以定点
表示的点组成以定点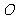 为圆心,半径为
为圆心,半径为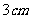 的圆.
的圆.
2.设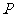 表示平面内的动点,属于下列集合的点组成什么图形?
表示平面内的动点,属于下列集合的点组成什么图形?
(1)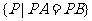
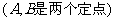 ;
;
(2)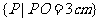
 .
.
1.解:(1)方程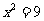 的解为
的解为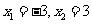 ,即集合
,即集合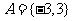 ;
;
(2)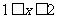 ,且
,且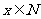 ,则
,则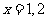 ,即集合
,即集合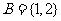 ;
;
(3)方程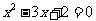 的解为
的解为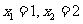 ,即集合
,即集合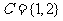 .
.
1.用列举法表示下列集合:
(1)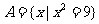 ;
;
(2)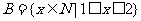 ;
;
(3)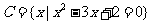 .
.
5.解决直线与二次曲线相交弦的问题,常“设而不求”,即将直线方程与二次曲线方程联立方程组,利用代入消元法转化为关于x(或y)的一元二次方程,将题中所给的几何量用韦达定理、△刻划出来;如:弦长|AB|=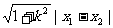 =
=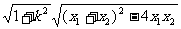 ,(其中k为直线AB的斜率),或|AB|=
,(其中k为直线AB的斜率),或|AB|=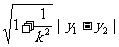 =
=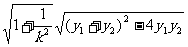 。涉及斜率及其弦中点的问题常用“点差法”,即设出弦的两端点坐标分别代入二次曲线方程作差,此后略作变化(分离出弦的斜率),即可得到弦的斜率与弦中点的横纵坐标之间的关系。
。涉及斜率及其弦中点的问题常用“点差法”,即设出弦的两端点坐标分别代入二次曲线方程作差,此后略作变化(分离出弦的斜率),即可得到弦的斜率与弦中点的横纵坐标之间的关系。
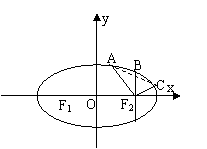
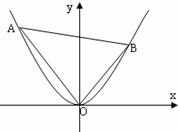 [举例1] 在平面直角坐标系xOy中,抛物线
[举例1] 在平面直角坐标系xOy中,抛物线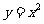 上异于坐标原点O的两不同动点A、B满足
上异于坐标原点O的两不同动点A、B满足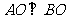 (如图所示).则
(如图所示).则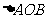 得重心G(即三角形三条中线的交点)的轨迹方程为 ;
得重心G(即三角形三条中线的交点)的轨迹方程为 ;
解析:显然直线AB的斜率存在,记为k,AB的方程记为:y=kx+b,(b≠0), A(x1,y1),B(x2,y2),将直线方程代入y=x2得:x2-kx-b=0,则有:⊿=k2+4b>0 ①,x1+x2=k ②, x1x2= -b ③,又y1=x12,y2=x22
∴y1y2=b2;而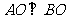
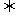 x1x2+ y1y2=0,得:-b+ b2=0且b≠0,∴b=1,代入①验证,满足;故y1+y2=k(x1+x2)+2=k2+2;设△AOB的重心为G(x,y),则x=
x1x2+ y1y2=0,得:-b+ b2=0且b≠0,∴b=1,代入①验证,满足;故y1+y2=k(x1+x2)+2=k2+2;设△AOB的重心为G(x,y),则x=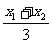 =
=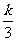 ④,
④,
y=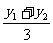 =
=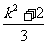 ⑤,由④⑤两式消去参数k得:G的轨迹方程为
⑤,由④⑤两式消去参数k得:G的轨迹方程为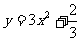 。
。
 注:上述求轨迹的方法称为“参数法”,一般先设法将动点坐标用“参数”表示,再消参数。
注:上述求轨迹的方法称为“参数法”,一般先设法将动点坐标用“参数”表示,再消参数。
[举例2]过椭圆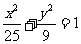 的右焦点F2并垂直于x轴
的右焦点F2并垂直于x轴
的直线与椭圆的一个交点为B,椭圆上不同的两点A(x1,y1),C(x2,y2)满足条件:|F2A|、|F2B|、|F2C|成等差
数列,则弦AC的中垂线在y轴上的截距的范围是 。
解析:对|F2A|+|F2C|=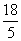 使用焦半径公式得:5-
使用焦半径公式得:5-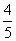 x1+5-
x1+5-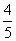 x2=
x2=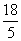
 x1+x2=8.此后,可以设AC的中垂线方程,代入椭圆方程,使用韦达定理;也可以用“点差”:记AC中点M(4,y0), 将A、C两点的坐标代入椭圆方程后作差得:
x1+x2=8.此后,可以设AC的中垂线方程,代入椭圆方程,使用韦达定理;也可以用“点差”:记AC中点M(4,y0), 将A、C两点的坐标代入椭圆方程后作差得:

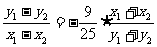 ,∴
,∴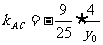 ,于是有:AC的中垂线的方程为:
,于是有:AC的中垂线的方程为:
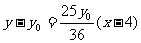 ,当x=0时:
,当x=0时: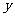 =-
=-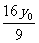 ,此即AC的中垂线在y轴上的截距,注意到:M(4,y0)在椭圆“内”,∴
,此即AC的中垂线在y轴上的截距,注意到:M(4,y0)在椭圆“内”,∴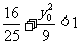 ,得-
,得-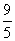 <
<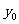 <
<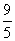 ,∴-
,∴-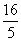 <-
<-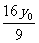 <
<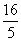 。
。
[巩固1]已知抛物线y2=4x,过点P(4,0)的直线与抛物线相交于A(x1,y1),B(x2,y2)两点,则y12+y22的最小值是 .
[巩固2]过抛物线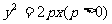 上一定点P(
上一定点P(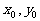 )(
)(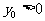 )作两条直线分别交抛物线于A(
)作两条直线分别交抛物线于A(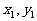 ),B(
),B(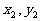 ),若PA与PB的斜率存在且倾斜角互补,则
),若PA与PB的斜率存在且倾斜角互补,则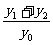 = 。
= 。
4.直线与圆锥曲线的公共点问题一般用方程组的解研究。直线与曲线有几个公共点,方程组就有几组解;直线与圆锥曲线相切体现为:在解方程组的过程中,“消元”后得到的一元二次方程有两个相等的实根,即⊿=0;抛物线的切线还可以用导数研究(视抛物线方程为二次函数)。
[举例1]设抛物线y2=8x的准线与x轴交于点Q,若过点Q的直线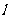 与抛物线有公共点,则直线
与抛物线有公共点,则直线 的斜率的取值范围是:( )
的斜率的取值范围是:( )
A.[-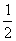 ,
,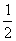 ] B.[-2,2] C.[-1,1] D.[-4,4]
] B.[-2,2] C.[-1,1] D.[-4,4]
解析:Q(-2,0),显然直线 斜率存在,记为k,则
斜率存在,记为k,则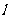 的方程为:y=k(x+2),代入抛物线方程得:k2x2+4(k2-2)x+4k2=0,①当k=0时,方程有解;②当k≠0时,⊿=64(1-k2)≥0即
的方程为:y=k(x+2),代入抛物线方程得:k2x2+4(k2-2)x+4k2=0,①当k=0时,方程有解;②当k≠0时,⊿=64(1-k2)≥0即
-1≤k<0或0<k≤,故选C。
[举例2]如图,设抛物线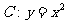 的焦点为F,动点P在直线
的焦点为F,动点P在直线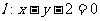 上运动,过P作抛物线C的两条切线PA、PB,且与抛物线C分别相切于A、B两点.则△APB的重心G的轨迹方程为
.
上运动,过P作抛物线C的两条切线PA、PB,且与抛物线C分别相切于A、B两点.则△APB的重心G的轨迹方程为
.
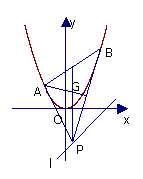 解析:设切点A、B坐标分别为
解析:设切点A、B坐标分别为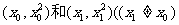 ,
,
∵y/=2x,∴两切线斜率分别为:2x0和2x1,
于是:切线AP的方程为:
切线BP的方程为: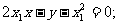
解得P点的坐标为: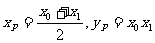
所以△APB的重心G的坐标为
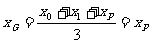 ,
,
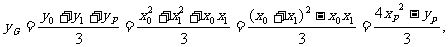
∴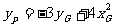 ,结合
,结合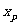 =
=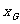 代入点P所在在直线方程,得到重心G的轨迹方程为:
代入点P所在在直线方程,得到重心G的轨迹方程为:
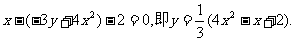
注:上述求轨迹的方法称为“代入法”,问题的基本结构是:动点N在已知曲线C0上移动,动点M随之移动(伴随点),求动点M的轨迹方程;一般解法是:寻找被动点M的坐标 (x,y)与主动点N的坐标(x0,y0)之间的关系,并用x,y表示x0,y0,再代入曲线C0的方程即可;此法为“参数法”的一种,借助M、N两点坐标之间的关系及曲线C0的方程消去两个参数x0,y0。
[巩固1] 已知直线 与抛物线
与抛物线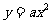 相切,则
相切,则
[巩固2]对于抛物线C:y2=4x,我们称满足y02<4x0的点M(x0,y0)在抛物线的内部.若点M(x0,y0)在抛物线内部,则直线l:y0y=2(x+ x0)与曲线C
A.恰有一个公共点 B.恰有2个公共点
C.可能有一个公共点,也可能有两个公共点 D.没有公共点
[迁移]直线y=ax+1与双曲线3x2-y2=1的两支分别交于A、B两点,则a的取值范围是 。
3.过抛物线y2=2px的焦点直线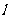 与抛物线y2=2px交于A(x1,y1)、B(x2,y2)两点,记住并会证明:
与抛物线y2=2px交于A(x1,y1)、B(x2,y2)两点,记住并会证明: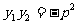 ,
,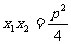 ,|AB|=
,|AB|= (其中
(其中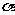 为弦AB的倾角,
为弦AB的倾角,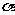 =900时的弦AB即为抛物线的通经),证明该结论时为避免讨论斜率不存在情形,可设直线方程为:x=my+
=900时的弦AB即为抛物线的通经),证明该结论时为避免讨论斜率不存在情形,可设直线方程为:x=my+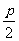 (其中m为AB的斜率的倒数);抛物线焦点弦问题常用定义,如:以焦点弦为直径的圆与准线相切。
(其中m为AB的斜率的倒数);抛物线焦点弦问题常用定义,如:以焦点弦为直径的圆与准线相切。
[举例1]抛物线y2=2px上弦长为a(a≥2p)的弦的中点到y轴的距离的最小值为: 。
解析:抛物线的准线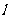 的方程为:x= -
的方程为:x= -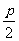 ,焦点F(
,焦点F(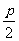 ,0),记弦的两端点为A、B,AB的中点为M,它们在
,0),记弦的两端点为A、B,AB的中点为M,它们在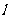 上的射影分别是A1,B1,M1;于是有:|AF|=|AA1|,|BF|=|BB1|,
上的射影分别是A1,B1,M1;于是有:|AF|=|AA1|,|BF|=|BB1|,
M到y轴的距离d=|MM1|-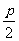 =
=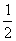 (|AA1|+|BB1|)-
(|AA1|+|BB1|)-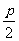 =
=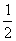 (|AF|+|BF|)-
(|AF|+|BF|)-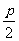 ≥
≥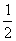 |AB|-
|AB|-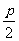
=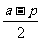 ,当且仅当A,B,F共线时等号成立。注:过焦点的弦最短是通经,长为2p,当
,当且仅当A,B,F共线时等号成立。注:过焦点的弦最短是通经,长为2p,当
a<2p时,A,B,F不可能共线。
[举例2] 给定抛物线C:y2=4x,F是C的焦点,过点F的直线l与C相交于A、B两点.设l的斜率为1,则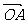 与
与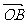 夹角为
;
夹角为
;
解析:抛物线的焦点为F(1,0),直线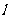 的方程为:x=y+1;将其代入抛物线方程得:y2-4y-4=0
的方程为:x=y+1;将其代入抛物线方程得:y2-4y-4=0
设A(x1,y1),B(x2,y2),则有y1+y2=4,y1y2=
-4,又x1=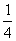 y12, x2=
y12, x2=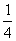 y22,∴x1 x2=
y22,∴x1 x2= (y1 y2)2=1.
(y1 y2)2=1.
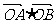 =(x1,y1)·(x2,y2)=x1x2+y1y2=
-3.
=(x1,y1)·(x2,y2)=x1x2+y1y2=
-3.
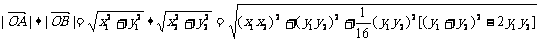
=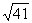 ,∴cos<
,∴cos<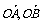 >=
>=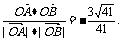 故
故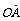 与
与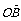 夹角为
夹角为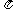 -arccos
-arccos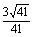 .
.
注:在研究形如y2=2px的抛物线与直线的有关问题时,设直线方程为x=my+b的形式,不仅可以简化计算,有时还可以避免对直线斜率是否存在的讨论。
[巩固1]AB是抛物线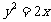 的一条焦点弦,|AB|=4,则AB中点C的横坐标是( )
的一条焦点弦,|AB|=4,则AB中点C的横坐标是( )
A.2 B.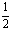 C.
C.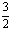 D.
D.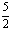
[巩固2]过抛物线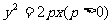 的焦点的直线
的焦点的直线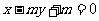 与抛物线交于A、B两点,且⊿OAB(O为坐标原点)的面积为
与抛物线交于A、B两点,且⊿OAB(O为坐标原点)的面积为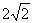 ,则m6+m4=
,则m6+m4=
2.涉及到抛物线上的点到焦点(准线)的距离问题常用定义;有时,抛物线上的点到与准线平行的直线的距离需转化为到准线的距离。
[举例1]已知A(3,1),抛物线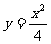 上一点P(x,y),则|PA|+y的最小值为 。
上一点P(x,y),则|PA|+y的最小值为 。
解析:抛物线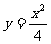 的准线为:y= -1,焦点F(0,1),记P在直线y= -1上的射影为Q,
的准线为:y= -1,焦点F(0,1),记P在直线y= -1上的射影为Q,
则y=|PQ|-1=|PF|-1,|PA|+y=|PA|+|PF|-1,问题转化为:求|PA|+|PF|的最小值,易见:
|PA|+|PF|≥|AF|=3,当且既当F、P、A共线时等号成立,故:|PA|+y的最小值为2。
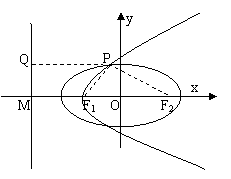 [举例2]已知椭圆E的离心率为e,两焦点为F1,F2,
[举例2]已知椭圆E的离心率为e,两焦点为F1,F2,
抛物线C以F1为顶点,F2为焦点,P为两曲线的一个
公共点,若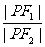 =e,则e的值为:
=e,则e的值为:
A. B.
B.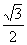 C.
C.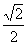 D.
D.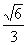
解析:记抛物线的准线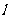 交x轴于M,P在
交x轴于M,P在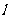 上的射影
上的射影
为Q,则|F1M|=|F1F2|=2c,即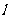 的方程为x= -3c,|PF2|=|PQ|,又
的方程为x= -3c,|PF2|=|PQ|,又
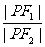 =e,即
=e,即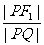 =e,∵F1是椭圆的左焦点,∴|PQ|为P到椭圆左准线的距离,即
=e,∵F1是椭圆的左焦点,∴|PQ|为P到椭圆左准线的距离,即
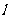 为椭圆的左准线,于是有:-3c= -
为椭圆的左准线,于是有:-3c= -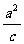
 e=
e= ,选A。
,选A。
[巩固1] 一动圆圆心在抛物线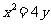 上,过点(0 , 1)且与定直线
上,过点(0 , 1)且与定直线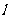 相切,则
相切,则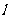 的方程为( )
的方程为( )
A.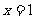 B.
B.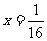 C.
C.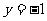 D.
D.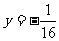
[巩固2] 椭圆C1: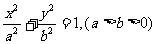 的左准线为
的左准线为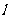 ,左、右焦点分别为F1,F2,抛物线C2的准线也为
,左、右焦点分别为F1,F2,抛物线C2的准线也为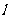 ,焦点为F2,记C1与C2的一个交点为P,则
,焦点为F2,记C1与C2的一个交点为P,则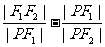 = ( )
= ( )
A.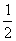 B.1 C.2
D.与a,b的取值有关
B.1 C.2
D.与a,b的取值有关
1.不要把抛物线的标准方程和二次函数的一般形式混为一谈;抛物线的焦点位置取决于哪个变量是一次的及其系数的正负;抛物线标准方程中的“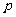 ”表示焦准距。
”表示焦准距。
[举例1] 抛物线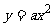 的准线方程为
的准线方程为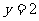 ,则
,则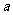 的值为
的值为
(A)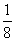 (B)
(B)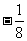 (C)
(C)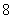 (D)
(D)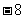
解析:抛物线的标准方程为: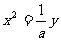 ,其准线方程为:y= -
,其准线方程为:y= -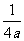 ,∴a=
,∴a= ,故选B。
,故选B。
[举例2]若椭圆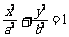 (a>b>0)的左、右焦点分别为F1、F2,线段F1F2被抛物线y2=2bx的焦点分成5∶3的两段,则此椭圆的离心率为 :
(a>b>0)的左、右焦点分别为F1、F2,线段F1F2被抛物线y2=2bx的焦点分成5∶3的两段,则此椭圆的离心率为 :
(A)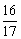 (B)
(B)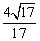 (C)
(C)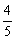 (D)
(D)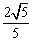
解析:抛物线y2=2bx的焦点为F(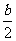 ,0),∵F将线段F1F2分成5∶3的两段,
,0),∵F将线段F1F2分成5∶3的两段,
∴(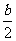 +c):(c -
+c):(c -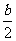 )=5∶3
)=5∶3 c=2b
c=2b e=
e=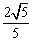 ,选D。
,选D。
[巩固1]点M(5,3)到抛物线y=ax2的准线的距离等于6,那么抛物线的方程是( )
(A)y=12x2 (B)y=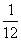 x2或y=-
x2或y=-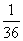 x2
(C)y=-36x2
(D)y=12x2或y=-36x2
x2
(C)y=-36x2
(D)y=12x2或y=-36x2
[巩固2] 若抛物线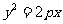 的焦点与椭圆
的焦点与椭圆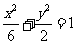 的右焦点重合,则
的右焦点重合,则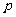 的值为
的值为
A. B.
B.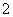 C.
C. D.
D.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com