第一节：单项填空(共20小题；每小题0.5分，满分10分)

1. ------_____ you were so late this morning?

　 ------I forgot to set the alarm before going to bed last night.

　 A. Why　　　　　　 B. How come　　 　C. How about　　 D. How

4．解：焦点的坐标为，不妨设直线为，

　　　 由，则直线为，

　　　 联合，即，

　　　 再由抛物线定义得，

　　　 而，得，

　　　 即，同理，

　　　 得，

　　　 所以当时，的最小值为．

4．过抛物线的焦点，作互相垂直的两条焦点弦和，

求的最小值．

3．解：解方程组，得，或，所以点的坐标是，

因为，所以的方程为，

由，得，或，

得点的坐标是，

即，

所以，所求抛物线的方程为．

3．直角三角形的三个顶点在抛物线上，直角顶点为原点，直角边所在的直线方程为，斜边的长为，求此抛物线的方程．

2．填空题

(1)若点到点的距离比它到定直线的距离小1，

则点的轨迹方程是　　　　 ．

(1)　　 由题意，点到点的距离等于它到定直线的距离，

根据抛物线的定义，，，得．

(2)抛物线过点，则的标准方程是　　　　 ．

(2)或　　 先设，则，得，即；

　　 　　　　　　　　　　　　　再设，则，得，即．

(3)是抛物线上的点，若到点的距离为15，则到直线

的距离是　　　　 ．

(3)　 抛物线的准线是，则到直线的距离是．

(4)若为抛物线上的动点，则到直线的距离的

最小值是　　　　 ，此时点的坐标为　　　　 ．

(4)　 　设抛物线上的点，

　　　　 　　　　．

　　　　　　　 取得最小值时，，即．

(5)已知直线与抛物线交于，两点，且经过抛物线的焦点，点坐标

为，则线段的中点到准线的距离是　　　　 ．

(5)　 抛物线的焦点为，准线为，而点坐标为，

　　 得直线的方程为，代人，得，

　　 即，则线段的中点到准线的距离是．

(6)已知圆与抛物线的准线相切，则　　　 ．

(6)　　 抛物线的准线为，

　　 　　　圆的标准方程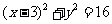为，即圆心为，

半径，，得．

1．选择题

(1)抛物线的顶点在原点，对称轴为轴，焦点在直线上，

则它的方程是(　　 )．

A．　　　 B．　　　 C．　　　 D．

(1)D　　 焦点为直线与轴的交点，即，得．

(2)焦点在，顶点在的抛物线方程是(　　 )．

A．　　　　　　　　　　　 B．

C．　　　　　　　　　　　 D．

(2)D　 顶点在，即向右平移个单位，即．

(3)已知抛物线的顶点为原点，焦点在轴上，抛物线上点到焦点的距离为，

则的值为(　　 )．

A．　　　　　 B．　　　　 　C．或　　　　　 D．或 　

(3)C　 抛物线上点到焦点的距离为，则抛物线上点到准线的

距离也为，得准线，即抛物线方程为，而点在抛物线上，

得．

(4)焦点在直线上的抛物线的标准方程为(　　 )．

A．或　　　　　　 B．或

C．或　　　　　 D．或

(4)C　　 当焦点为时，，得抛物线为；

　　　　　 当焦点为时，，得抛物线为．

(5)若抛物线上横坐标为的点到焦点的距离等于，

则焦点到准线的距离是(　　 )．

A．　　　　　　 B．　　　　　 C．　　　　　　 D．

(5)B　 横坐标为的点到焦点的距离等于，该点到准线的距离也是，

得准线，即．

(6)过抛物线的焦点作直线交抛物线于两点，若，则等于(　　 )．

A．　　　　　　 B．　　　　　 C．　　　　　　 D．

(6)A　 抛物线的准线方程是，由抛物线的定义知，抛物线上的点

到焦点的距离等于到准线的距离，所以．

24.选修4-5不等式选讲(本小题10分)

设函数f(x)= ｜2x+1｜-｜x-4｜.

(1)解不等式f(x)＞2；

(2)求函数y= f(x)的最小值．

23.选修4－4：坐标系与参数方程(本小题10分)

　 已知某条曲线C的参数方程为(其中t是参数，a∈R)，点M(5，4)在该曲线上

(1)求常数a；(2)求曲线C的普通方程．

22. 选修4－1：几何证明选讲(本小题10分)

如图，ABC内接于⊙O，AB⊥CD于D，E在⊙O上，AE交CD于G，求证：AC²=AG·AE．