
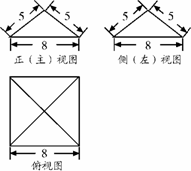
4.一个几何体的三视图如图所示,那么此几何体
的侧面积(单位: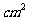 )为( )
)为( )
A. 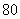 |
B.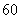 |
C. 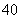 |
D.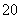 |
3.已知平面向量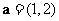 ,
, 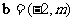 , 且
, 且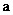 ∥
∥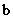 , 则
, 则 的值为( )
的值为( )
A. |
 B. B.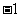 |
C.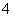 |
D. |
2.已知命题 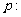
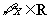 ,
,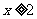 ,那么命题
,那么命题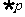 为( )
为( )
A.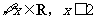 |
B.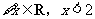 |
C.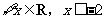 |
D. |
1.复数 等于( )
等于( )
A.
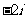 |
B.
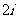 |
C.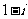 |
D.
 |
(15)(本小题满分13分)
在 中,角
中,角 ,
, ,
, 所对的边分别为
所对的边分别为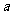 ,
,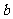 ,
,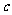 ,且
,且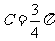 ,
,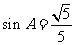 .
.
(Ⅰ)求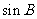 的值;
的值;
(Ⅱ)若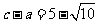 ,求
,求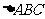 的面积.
的面积.
(16) (本小题满分13分)
在某校组织的一次篮球定点投篮比赛中,两人一对一比赛规则如下:若某人某次投篮命中,则由他继续投篮,否则由对方接替投篮. 现由甲、乙两人进行一对一投篮比赛,甲和乙每次投篮命中的概率分别是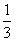 ,
,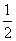 .两人共投篮3次,且第一次由甲开始投篮. 假设每人每次投篮命中与否均互不影响.
.两人共投篮3次,且第一次由甲开始投篮. 假设每人每次投篮命中与否均互不影响.
(Ⅰ)求3次投篮的人依次是甲、甲、乙的概率;
(Ⅱ)若投篮命中一次得1分,否则得0分. 用ξ表示甲的总得分,求ξ的分布列和数学期望.
(17) (本小题满分14分)
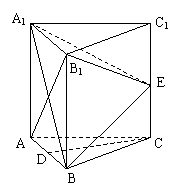 如图,在三棱柱
如图,在三棱柱 中,每个侧面均为正方形,
中,每个侧面均为正方形,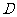 为底边
为底边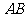 的中点,
的中点,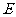 为侧棱
为侧棱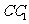 的中点.
的中点.
(Ⅰ)求证: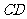 ∥平面
∥平面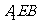 ;
;
(Ⅱ)求证: 平面
平面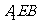 ;
;
(Ⅲ)求直线 与平面
与平面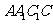 所成角的正弦值.
所成角的正弦值.
(18)(本小题满分13分)
已知函数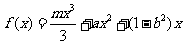 ,
,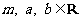 .
.
(Ⅰ)求函数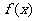 的导函数
的导函数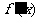 ;
;
(Ⅱ)当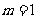 时,若函数
时,若函数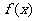 是
是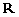 上的增函数,求
上的增函数,求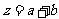 的最小值;
的最小值;
(Ⅲ)当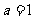 ,
,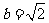 时,函数
时,函数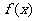 在
在 上存在单调递增区间,求
上存在单调递增区间,求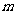 的取值范围.
的取值范围.
(19)(本小题满分13分)
已知中心在原点,焦点在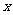 轴上的椭圆
轴上的椭圆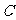 的离心率为
的离心率为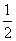 ,且经过点
,且经过点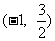 ,过点
,过点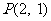 的直线
的直线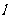 与椭圆
与椭圆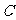 在第一象限相切于点
在第一象限相切于点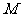 .
.
(Ⅰ)求椭圆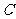 的方程;
的方程;
(Ⅱ)求直线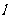 的方程以及点
的方程以及点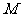 的坐标;
的坐标;
(Ⅲ)是否存在过点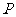 的直线
的直线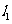 与椭圆
与椭圆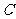 相交于不同的两点
相交于不同的两点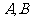 ,满足
,满足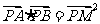 ?若存在,求直线
?若存在,求直线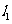 的方程;若不存在,请说明理由.
的方程;若不存在,请说明理由.
(20)(本小题满分14分)
若一个数列各项取倒数后按原来的顺序构成等差数列,则称这个数列为调和数列.已知数列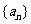 是调和数列,对于各项都是正数的数列
是调和数列,对于各项都是正数的数列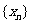 ,满足
,满足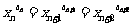
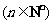 .
.
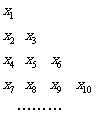 (Ⅰ)证明数列
(Ⅰ)证明数列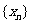 是等比数列;
是等比数列;
(Ⅱ)把数列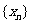 中所有项按如图所示的规律排成一个三角形
中所有项按如图所示的规律排成一个三角形
数表,当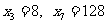 时,求第
时,求第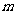 行各数的和;
行各数的和;
(Ⅲ)对于(Ⅱ)中的数列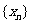 ,证明:
,证明: .
.
(考生务必将第Ⅱ卷所有题目的答案写在答题卡上,在试卷上作答无效)
(9)已知圆的极坐标方程为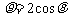 ,则圆心的直角坐标是
;半径长
,则圆心的直角坐标是
;半径长
为 .
(10)圆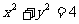 被直线
被直线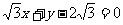 截得的劣弧所对的圆心角的大小为
.
截得的劣弧所对的圆心角的大小为
.
 (11)已知向量
(11)已知向量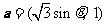 ,
,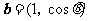 ,则
,则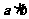 的最大值为
.
的最大值为
.
(12)如图,圆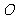 是
是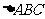 的外接圆,过点C的切线交
的外接圆,过点C的切线交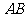
的延长线于点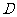 ,
,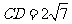 ,
,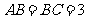 .则
.则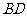
的长为
;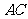 的长为
.
的长为
.

(13)右边程序框图的程序执行后输出的结果是 .
(14)一个数字生成器,生成规则如下:第1次生成一个数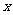 ,以后
,以后
每次生成的结果是将上一次生成的每一个数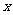 生成两个数,一
生成两个数,一
个是  ,另一个是
,另一个是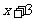 .设第
.设第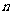 次生成的数的个数为
次生成的数的个数为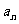 ,
,
则数列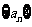 的前
的前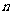 项和
项和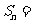 ;若
;若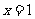 ,前
,前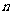 次
次
生成的所有数中不同的数的个数为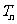 ,则
,则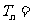 .
.
(1)复数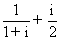 等于
等于
(A)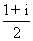 (B)
(B)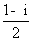 (C)-
(C)-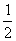 (D)
(D)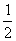
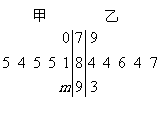
(2)右图是2010年青年歌手大奖赛中,七位评委为甲、乙两
名选手打出的分数的茎叶图(其中m为数字0-9中的
一个),去掉一个最高分和一个最低分后,甲、乙两名选
手得分的平均数分别为a1,a2,则一定有
(A)a1>a2 (B)a2>a1
(C)a1=a2 (D)a1,a2的大小与m的值有关
(3)下列函数中,最小正周期为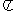 ,且图象关于直线
,且图象关于直线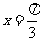 对称的是
对称的是
(A)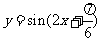 (B)
(B)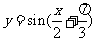
(C)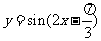 (D)
(D)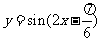

 (4)一个简单几何体的正视图、侧视图如图所示,则其俯视图不可能为①长方形;②正方
(4)一个简单几何体的正视图、侧视图如图所示,则其俯视图不可能为①长方形;②正方
形;③圆;④椭圆. 其中正确的是
(A)①② (B) ②③
(C)③④ (D) ①④
(5)在区间[-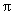 ,
,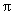 ]内随机取两个数分别记为a,b,则使得函数
]内随机取两个数分别记为a,b,则使得函数 有零点的概率为
有零点的概率为
(A)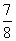 (B)
(B)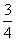 (C)
(C)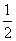 (D)
(D)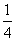
(6)已知点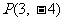 是双曲线
是双曲线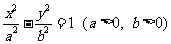 渐近线上的一点,
渐近线上的一点,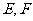 是左、右两个焦点,若
是左、右两个焦点,若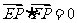 ,则双曲线方程为
,则双曲线方程为
(A)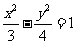 (B)
(B)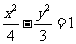
(C)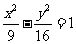 (D)
(D)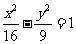
(7)设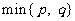 表示
表示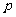 ,
,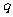 两者中的较小的一个,若函数
两者中的较小的一个,若函数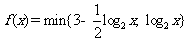
,则满足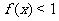 的
的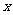 的集合为
的集合为
(A)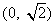 (B)
(B)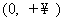
(C)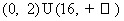 (D)
(D)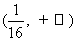
(8)一个空间四边形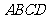 的四条边及对角线
的四条边及对角线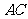 的长均为
的长均为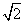 ,二面角
,二面角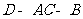 的
的
余弦值为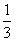 ,则下列论断正确的是
,则下列论断正确的是
(A)空间四边形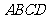 的四个顶点在同一球面上且此球的表面积为
的四个顶点在同一球面上且此球的表面积为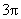
(B)空间四边形 的四个顶点在同一球面上且此球的表面积为
的四个顶点在同一球面上且此球的表面积为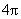
(C)空间四边形 的四个顶点在同一球面上且此球的表面积为
的四个顶点在同一球面上且此球的表面积为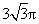
(D)不存在这样的球使得空间四边形 的四个顶点在此球面上
的四个顶点在此球面上
第II卷(非选择题 共110分)
(15)(本小题满分13分)
在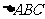 中,角
中,角 ,
,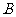 ,
,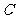 所对的边分别为
所对的边分别为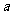 ,
,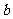 ,
,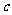 ,且
,且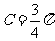 ,
,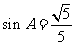 .
.
(Ⅰ)求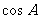 ,
,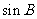 的值;
的值;
(Ⅱ)若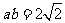 ,求
,求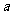 ,
,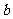 的值.
的值.
(16)(本小题满分13分)
袋子中装有编号为a,b的2个黑球和编号为c,d,e的3个红球,从中任意摸出2个球.
(Ⅰ)写出所有不同的结果;
(Ⅱ)求恰好摸出1个黑球和1个红球的概率;
(Ⅲ) 求至少摸出1个黑球的概率.
(17)(本小题满分13分)
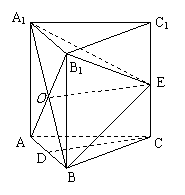 如图,在三棱柱
如图,在三棱柱 中,每个侧面均为正方形,
中,每个侧面均为正方形, 为底边
为底边 的中点,
的中点,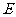 为侧棱
为侧棱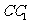 的中点,
的中点,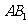 与
与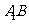 的交点为
的交点为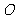 .
.
(Ⅰ)求证: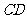 ∥平面
∥平面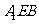 ;
;
(Ⅱ)求证: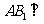 平面
平面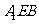 .
.
(18)(本小题满分14分)
已知函数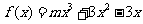 ,
,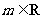 .
.
(Ⅰ)若函数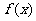 在
在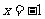 处取得极值,试求
处取得极值,试求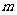 的值,并求
的值,并求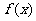 在点
在点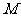
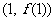 处的切线方程;
处的切线方程;
(Ⅱ)设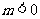 ,若函数
,若函数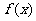 在
在 上存在单调递增区间,求
上存在单调递增区间,求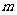 的取值范围.
的取值范围.
(19)(本小题满分13分)
已知中心在原点,焦点在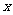 轴上的椭圆
轴上的椭圆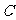 的离心率为
的离心率为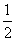 ,且经过点
,且经过点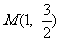 ,过点
,过点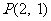 的直线
的直线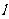 与椭圆
与椭圆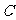 相交于不同的两点
相交于不同的两点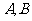 .
.
(Ⅰ)求椭圆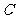 的方程;
的方程;
(Ⅱ)是否存直线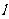 ,满足
,满足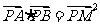 ?若存在,求出直线
?若存在,求出直线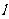 的方程;若不存在,请说明理由.
的方程;若不存在,请说明理由.
(20)(本小题满分14分)
若一个数列各项取倒数后按原来的顺序构成等差数列,则称这个数列为调和数列.已知数列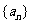 是调和数列,对于各项都是正数的数列
是调和数列,对于各项都是正数的数列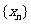 ,满足
,满足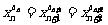
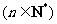 .
.
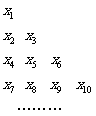 (Ⅰ)求证:数列
(Ⅰ)求证:数列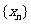 是等比数列;
是等比数列;
(Ⅱ)把数列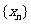 中所有项按如图所示的规律排成一个三角形数表,
中所有项按如图所示的规律排成一个三角形数表,
当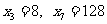 时,求第
时,求第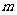 行各数的和;
行各数的和;
(Ⅲ)对于(Ⅱ)中的数列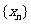 ,若数列
,若数列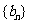 满足
满足
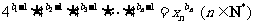 ,求证:数列
,求证:数列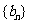 为等差数列.
为等差数列.
(考生务必将第Ⅱ卷所有题目的答案写在答题卡上,在试卷上作答无效)
(9)函数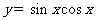 的最大值是 .
的最大值是 .
(10)在抛物线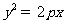 上,横坐标为4的点到焦点的距离为5,则
上,横坐标为4的点到焦点的距离为5,则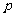 的值为
的值为 .
.
(11)左下程序框图的程序执行后输出的结果是 .


(12)如右上图所示,一个空间几何体的正视图和侧视图都是边长为1的正方形,俯视图是一个直径为1的圆,那么这个几何体的全面积为 .
(13)圆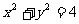 被直线
被直线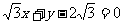 截得的劣弧所对的圆心角的大小为 .
截得的劣弧所对的圆心角的大小为 .
(14)一个数字生成器,生成规则如下:第1次生成一个数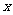 ,以后每次生成的结果可将上一次生成的每一个数
,以后每次生成的结果可将上一次生成的每一个数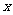 生成两个数,一个是
生成两个数,一个是  ,另一个是
,另一个是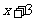 .设第
.设第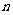 次生成的数的个数为
次生成的数的个数为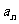 ,则数列
,则数列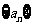 的前
的前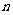 项和
项和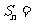 _________________;若
_________________;若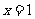 ,前
,前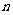 次生成的所有数中不同的数的个数为
次生成的所有数中不同的数的个数为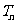 ,则
,则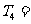 ______________________.
______________________.
4个选项中,只有一项是符合题目要求的.
(1)复数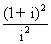 等于
等于
(A)2
(B)-2 (C)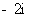 (D)
(D)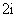
(2)命题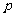 :
: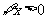 ,都有
,都有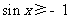 ,则
,则
(A)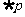 :
: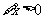 ,使得
,使得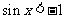 (B)
(B)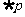 :
: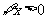 ,都有
,都有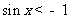
(C)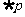 :
: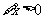 ,使得
,使得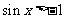 (D)
(D)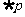 :
: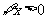 ,都有
,都有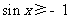
(3)满足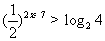 成立的
成立的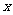 的取值范围是
的取值范围是
(A)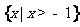 (B)
(B)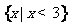
(C)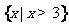 (D)
(D)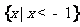
(4)下列函数中,最小正周期为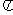 ,且图象关于直线
,且图象关于直线 对称的是
对称的是
(A)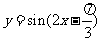 (B)
(B)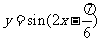
(C)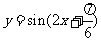 (D)
(D)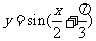
(5)一只小蜜蜂在一个棱长为30的正方体玻璃容器内随机飞行,若蜜蜂在飞行过程中与正方体玻璃容器6个表面中至少有一个的距离不大于10,则就有可能撞到玻璃上而不安全;若始终保持与正方体玻璃容器6个表面的距离均大于10,则飞行是安全的,假设蜜蜂在正方体玻璃容器内飞行到每一位置可能性相同,那么蜜蜂飞行是安全的概率是
(A) 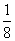 (B)
(B) 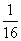 (C)
(C) 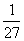 (D)
(D) 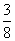
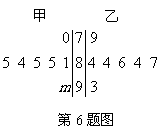
(6)右图是某年青年歌手大奖赛中,七位评委为甲乙两名选手打出的分数的茎叶图(其中m为数字0-9中的一个),去掉一个最高分和一个最低分后,甲、乙两名选手得分的平均数分别为a1,a2,则一定有
(A)a1>a2 (B)a1<a2
(C)a1=a2 (D)a1,a2的大小与m的值有关
(7)设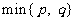 表示
表示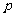 ,
,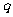 两者中的较小者,若函数
两者中的较小者,若函数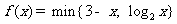 ,则满足
,则满足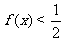 的
的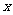 的集合为
的集合为
(A)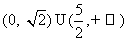 (B)
(B)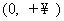
(C)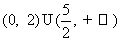 (D)
(D)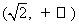
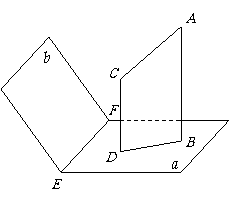 (8)如图,设平面
(8)如图,设平面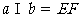 ,
, ,
,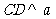 ,垂足分别为
,垂足分别为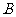 ,
,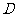 ,且
,且 .如果增加一个条件就能推出
.如果增加一个条件就能推出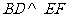 ,给出四个条件:①
,给出四个条件:①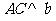 ;②
;②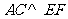 ;③
;③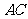 与
与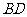 在
在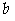 内的正投影在同一条直线上 ;④
内的正投影在同一条直线上 ;④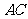 与
与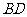 在平面
在平面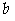 内的正投影所在的直线交于一点. 那么这个条件不可能是
内的正投影所在的直线交于一点. 那么这个条件不可能是
(A)①② (B)②③
(C)③ (D)④
第II卷(非选择题 共110分)
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com