
1、(12分)已知某职业技能训练班学生的项目A和项目B成绩抽样统计表如下,抽出学生n人,成绩只有3,4,5三种分值。设x,y分别表示项目A和项目B成绩。例如:表中项目A成绩为5分的共7+9+4=20人。已知x=4且y=5的概率是 0.2.
(1)求n(2)若在该样本中,再按项目B的成绩分层抽样出20名学生,则y=3的学生中应抽出多少人?(3)已知a 9,b
9,b 2,项目B为3分的学生中,求项目A得3分的人数比得4分的人数多的概率。
2,项目B为3分的学生中,求项目A得3分的人数比得4分的人数多的概率。
 人数 x 人数 x y |
5 |
4 |
3 |
|
5 |
7 |
20 |
5 |
|
4 |
9 |
18 |
6 |
|
3 |
4 |
a |
b |
3.(本小题满分13分)
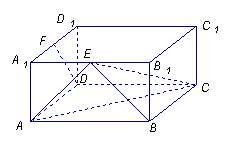 如图,在长方体
如图,在长方体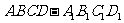 中,
中,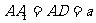 ,
,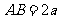 ,
,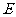 、
、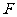 分别为
分别为 、
、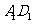 的中点.
的中点.
(Ⅰ)求证: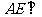 平面
平面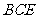 ;
;
(Ⅱ)求证: 平面
平面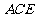 .
.
2.(本题14分)已知函数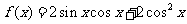 (
(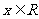 ).
).
(Ⅰ)求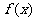 的最小正周期,并求
的最小正周期,并求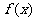 的最小值;
的最小值;
(Ⅱ)令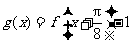 ,判断函数
,判断函数 的奇偶性,并说明理由.
的奇偶性,并说明理由.
1.(本题14分)从装有编号分别为a,b的2个黄球和编号分别为 c,d的2个红球的袋中无放回地摸球,每次任摸一球,求:
(Ⅰ)第1次摸到黄球的概率;
(Ⅱ)第2次摸到黄球的概率.
20、(14分)设集合W由满足下列两个条件的数列 构成:
构成:
①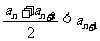 ;②存在实数M,使
;②存在实数M,使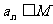 。(n为正整数)
。(n为正整数)
(Ⅰ)在只有5项的有限数列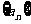 、
、 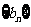 中,其中
中,其中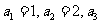 =3,
=3,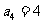 ,
,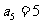 ;
;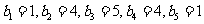 ;试判断数列
;试判断数列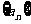 、
、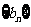 是否为集合W中的元素;
是否为集合W中的元素;
(Ⅱ)设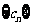 是各项为正数的等比数列,
是各项为正数的等比数列,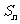 是其前
是其前 项和,
项和,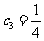 ,
,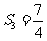 ,试证明
,试证明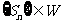 ,并写出
,并写出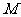 的取值范围;
的取值范围;
(Ⅲ)设数列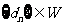 ,对于满足条件的M的最小值M0,都有
,对于满足条件的M的最小值M0,都有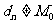 (
(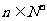 )。
)。
求证:数列 单调递增。
单调递增。
19、(13分)在直角坐标系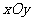 中,点
中,点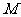 到F1
到F1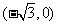 、F2
、F2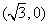 的距离之和是4,点
的距离之和是4,点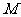 的轨迹
的轨迹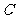 与
与 轴的负半轴交于点
轴的负半轴交于点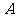 ,不过点
,不过点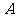 的直线
的直线 :
: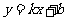 与轨迹
与轨迹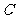 交于不同的两点
交于不同的两点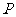 和
和 .
.
(1)求轨迹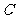 的方程;
的方程;
(2)当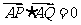 时,求
时,求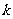 与
与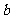 的关系,并证明直线
的关系,并证明直线 过定点.
过定点.
18、(13分)已知函数 。
。
(Ⅰ)当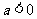 时,求函数f(x)的单调区间;
时,求函数f(x)的单调区间;
(Ⅱ)若函数f(x)在[1,e]上的最小值是 ,求
,求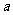 的值.
的值.
17、(14分)某工厂师徒二人各加工相同型号的零件2个,是否加工出精品均互不影响。已知师父加工一个零件是精品的概率为 ,师徒二人各加工2个零件都是精品的概率为
,师徒二人各加工2个零件都是精品的概率为 。
。
(Ⅰ)求徒弟加工2个零件都是精品的概率;
(Ⅱ)求徒弟加工该零件的精品数多于师父的概率;
(Ⅲ)设师徒二人加工出的4个零件中精品个数为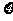 ,求
,求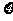 的分布列与均值
的分布列与均值 。
。
16、(14分)如图,在底面是正方形的四棱锥P-ABCD中,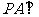 面ABCD,BD交AC于点E,F是PC中点,G为AC上一点。
面ABCD,BD交AC于点E,F是PC中点,G为AC上一点。
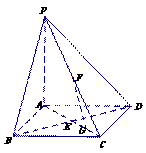 (Ⅰ)求证:BD
(Ⅰ)求证:BD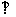 FG;
FG;
(Ⅱ)确定点G在线段AC上的位置,使FG//平面PBD,并说明理由;
(Ⅲ)当二面角B-PC-D的大小为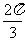 时,求PC与底面ABCD所成角的正切值。
时,求PC与底面ABCD所成角的正切值。
15、(12分)已知函数f(x)=asinx+bcosx的图象经过点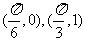 。
。
(Ⅰ)求实数a,b的值;
(Ⅱ)若xÎ[0,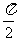 ],求函数f(x)的最大值及此时x的值。
],求函数f(x)的最大值及此时x的值。
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com