
2.(满分12分)现有2009年全运会志愿者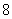 名,其中志愿者
名,其中志愿者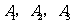 通晓日语,
通晓日语,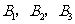 通晓俄语,
通晓俄语,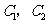 通晓韩语.从中选出通晓日语、俄语和韩语的志愿者各
通晓韩语.从中选出通晓日语、俄语和韩语的志愿者各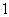 名,组成一个小组.
名,组成一个小组.
(1)求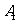 被选中的概率;
被选中的概率;
(2)求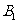 和
和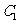 不全被选中的概率.
不全被选中的概率.
3.连续抛掷一枚均匀的骰子(各个面上分别标有数字1,2,3,4,5,6)两次,用(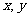 )表示结果,其中
)表示结果,其中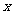 表示第一次向上的点数,
表示第一次向上的点数,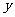 表示第二次向上的点数。
表示第二次向上的点数。
(1)试问:一共有多少种不同的结果?请列出所有可能的结果;
(2)若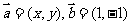 ,试求满足
,试求满足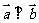 的概率。
的概率。
1(满分12分)△ABC中,a、b、c分别是角A、B、C的对边,若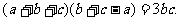
(1)求角A的值;
(2)在(1)的结论下,若0≤x≤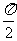 ,求y=cos2x+sinA•sin2x的最值。
,求y=cos2x+sinA•sin2x的最值。
2. (本小题满分12分)
(本小题满分12分)
如图,已知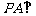 ⊙O所在的平面,
⊙O所在的平面,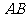 是⊙O的直径,
是⊙O的直径,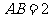 ,
,
C是⊙O上一点,且 ,
,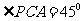
是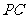 中点.F为PB中点.
中点.F为PB中点.
(Ⅰ) 求证: 
(Ⅱ) 求证: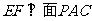 ;
;
(Ⅲ)求三棱锥B-PAC的体积.
1.已知向量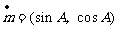 ,
, ,
,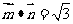 ,且A为锐角.
,且A为锐角.
(1)求角A的大小; (2) 求函数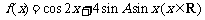 的值域.
的值域.
3.(本小题满分12分)
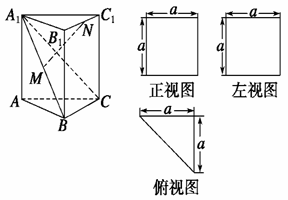 一个多面体的直观图和三视图(正视图、左视图、俯视图)如图所示,M、N分别为A1B、B1C1的中点.求证:
一个多面体的直观图和三视图(正视图、左视图、俯视图)如图所示,M、N分别为A1B、B1C1的中点.求证:
(1)MN∥平面ACC1A1
(2)MN⊥平面A1BC.
(3)求多面体A1B1BC的体积
2.(12分)奇瑞公司生产的“奇瑞”轿车是我国民族品牌.该公司2009年生产的“旗云”、“风云”、“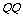 ”三类经济型轿车中,每类轿车均有舒适和标准两种型号.某周产量如下表:
”三类经济型轿车中,每类轿车均有舒适和标准两种型号.某周产量如下表:
|
l 车型 |
l 旗云 |
l 风云 |
l 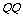 |
|
l 舒适 |
l 100 |
l 150 |
l 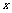 |
|
l 标准 |
l 300 |
l 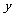 |
l 600 |
若按分层抽样的方法在这一周生产的轿车中抽取50辆进行检测,则必须抽取“旗云”轿车10辆,“风云”轿车15辆.
⑴求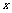 、
、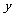 的值;
的值;
⑵在年终促销活动中,奇瑞公司奖给了某优秀销售公司2辆舒适型和3辆标准型“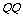 ”轿车,该销售公司又从中随机抽取了2辆作为奖品回馈消费者.求至少有一辆是舒适型轿车的概率.
”轿车,该销售公司又从中随机抽取了2辆作为奖品回馈消费者.求至少有一辆是舒适型轿车的概率.
1. (12分)已知向量
(12分)已知向量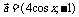 ,
,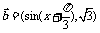 ,且
,且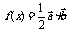 .
.
⑴求函数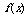 的解析式,并指出其单调递增区间;
的解析式,并指出其单调递增区间;
⑵画出函数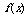 在区间
在区间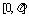 上的图像.
上的图像.
3. (本小题满分13分)
某研究性学习小组对春季昼夜温差大小与某花卉种子发芽多少之间的关系进行研究,他们分别记录了3月1日至3月5日的每天昼夜温差与实验室每天每100颗种子浸泡后的发芽数,得到如下资料:
|
日期 |
3月1日 |
3月2日 |
3月3日 |
3月4日 |
3月5日 |
|
温差(℃) |
10 |
11 |
13 |
12 |
8 |
|
发芽数(颗) |
23 |
25 |
30 |
26 |
16 |
(1) 求这5天的平均发芽率;
(2) 从3月1日至3月5日中任选2天,记前面一天种子数为,后面一天种子数好似,用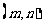 的形式列出所有基本事件,并求满足“
的形式列出所有基本事件,并求满足“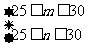 ”的概率。
”的概率。
1.(本小题满分13分)已知函数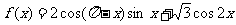 .
.
(1)求函数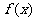 的最小正周期;
的最小正周期;
(2)求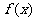 的对称中心的坐标;
的对称中心的坐标;
(3) 设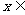
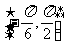 ,求函数
,求函数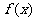 的单调区间.
的单调区间.
2(本小题满分14分).如图,在直三棱柱(侧棱与底面垂直的三棱柱)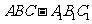 中,
中,
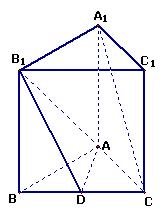
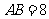 ,
,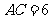 ,
,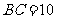 ,
,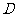 是
是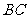 边的中点.
边的中点.
(Ⅰ)求证: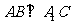 ;
;
(Ⅱ)求证: ∥ 面
∥ 面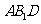 ;
;
2.(本小题满分12分)甲、乙两位同学参加数学竞赛培训,在培训期间,他们参加的5次模考成绩记录如下:
甲 82 82 79 95 87
乙 95 75 80 90 85
(Ⅰ)求乙同学五次模考成绩的标准差;
(Ⅱ)从甲、乙两人的成绩中各随机抽取一个,求甲的成绩比乙高的概率。
3(本小题满分12分)下图是一几何体的直观图、主视图、俯视图、左视图.
(Ⅰ)若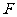 为
为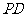 的中点,求证:
的中点,求证: 面
面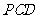 ;
;
(Ⅱ)求三棱锥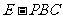 的体积.
的体积.

湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com