
20. (本小题满分14分)
如图,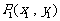 、
、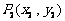 、…、
、…、 (
( )是曲线
)是曲线 :
:
 (
( )上的
)上的 个点,点
个点,点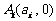 (
( )在
)在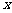 轴的正半轴上,且
轴的正半轴上,且 是正三角形(
是正三角形(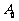 是坐标原点).
是坐标原点).
(Ⅰ) 写出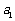 ,
,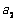 ,
, ;
;
(Ⅱ) 求出点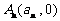 (
(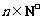 )的横坐标
)的横坐标 关于
关于 的表达式;
的表达式;
(Ⅲ) 设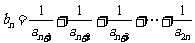 ,若对任意的正整数
,若对任意的正整数 ,当
,当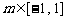 时,不等式
时,不等式 恒成立,求实数
恒成立,求实数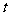 的取值范围.
的取值范围.
19. (本小题满分14分)
设直线 与椭圆
与椭圆 相交于A、B两个不同的点,与x轴相交于点C,记O为坐标原点.
相交于A、B两个不同的点,与x轴相交于点C,记O为坐标原点.
(1)证明: ;
;
(2)若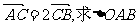 的面积取得最大值时的椭圆方程.
的面积取得最大值时的椭圆方程.
18. (本小题满分14分)
已知函数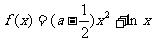 .(
.( R)
R)
(Ⅰ) 当 时,求
时,求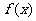 在区间[1,e]上的最大值和最小值;
在区间[1,e]上的最大值和最小值;
(Ⅱ)若在区间(1,+∞)上,函数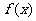 的图象恒在直线
的图象恒在直线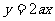 下方,求
下方,求 的取值范围.
的取值范围.
17. (本小题满分13分)
如图,已知四棱锥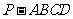 的底面是正方形,
的底面是正方形,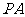 ⊥底面
⊥底面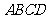 ,且
,且 ,点
,点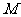 、
、 分别在侧棱
分别在侧棱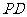 、
、 上,且
上,且

(Ⅰ)求证: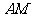 ⊥平面
⊥平面 ;
;
(Ⅱ)若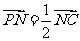 ,求平面
,求平面 与平面
与平面 的所成锐二面角的余弦值。
的所成锐二面角的余弦值。
16. (本小题满分13分)
已知函数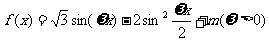 的最小正周期为
的最小正周期为 ,当
,当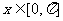 时,函数
时,函数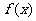 的最小值为0.
的最小值为0.
(Ⅰ)求函数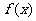 的表达式;
的表达式;
(Ⅱ)在△ABC中,若 的值.
的值.
15. (本小题满分12分)
某校从参加高一年级期末考试的学生中抽出60名学生,将其成绩(均为整数)分成六段 ,
,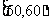 ,…,
,…,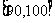 后画出如下部分频率分布直方图.观察图形的信息,回答下列问题:
后画出如下部分频率分布直方图.观察图形的信息,回答下列问题:
(Ⅰ) 求第四小组的频率,并补全这个频率分布直方图;
 (Ⅱ) 从成绩是70分以上(包括70分)的学生中选两人,求这两人的成绩在
(Ⅱ) 从成绩是70分以上(包括70分)的学生中选两人,求这两人的成绩在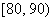 内的人数的分布列及期望.
内的人数的分布列及期望.
14.在数列 中,如果存在非零常数T,使得
中,如果存在非零常数T,使得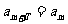 对任意正整数m均成立,那么就称
对任意正整数m均成立,那么就称 为周期数列,其中T叫做数列
为周期数列,其中T叫做数列 的周期. 已知数列
的周期. 已知数列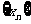 满足
满足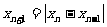 (
( N
N ),且
),且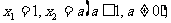 当数列
当数列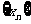 周期为3时,则该数列的前2007项的和为
.
周期为3时,则该数列的前2007项的和为
.
13.曲线 :
: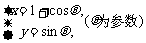 上的点到曲线
上的点到曲线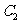 :
: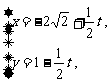
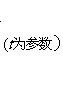 上的点的最短离为
.
上的点的最短离为
.
12.某高三学生希望报名参加6所高校中的3所学校
的自主招生考试,由于其中两所学校的考试时间
相同,因此该学生不能同时报考这两所学校.该
学生不同的报考方法种数是 .
(用数字作答)
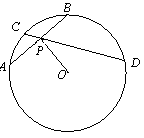
11.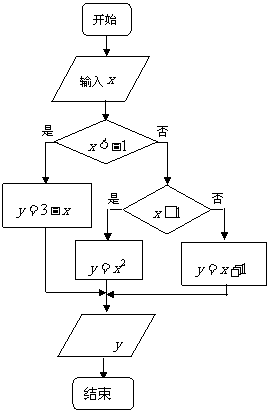 如图,⊙
如图,⊙ 的两条弦
的两条弦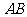 ,
,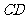 相交于圆内一点
相交于圆内一点 ,若
,若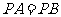 ,
,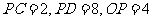 ,则该圆的半径长为
.
,则该圆的半径长为
.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com