
16.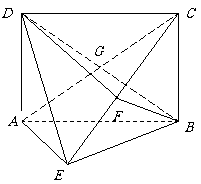 解:(Ⅰ)证明:
解:(Ⅰ)证明:
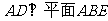 ,
,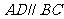
∴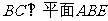 ,则
,则
又
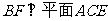 ,则
,则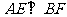
∴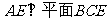 ………………………………4分
………………………………4分
(Ⅱ)证明:依题意可知: 是
是 中点
中点

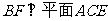 则
则 ,而
,而
∴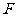 是
是 中点 …………………………………6分
中点 …………………………………6分
在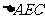 中,
中,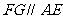
∴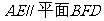 ……………………………………………8分
……………………………………………8分
(Ⅲ)解:
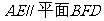
∴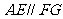 ,而
,而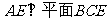
∴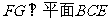 ∴
∴ ……………………10分
……………………10分

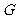 是
是 中点
中点
∴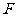 是
是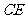 中点 ∴
中点 ∴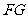
 且
且

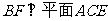 ∴
∴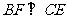
∴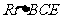 中,
中,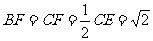
∴ ……………………………………………12分
……………………………………………12分
∴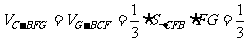 ………………………………14分
………………………………14分

15. (Ⅰ)
 , ……………………………2分
, ……………………………2分
 ,…………………………………4分
,…………………………………4分
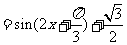 ,…………………………………………6分
,…………………………………………6分
∴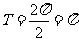 ………………………………………………………7分
………………………………………………………7分
(Ⅱ)∵  ∴
∴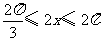
∴ ………………………………………………………8分
………………………………………………………8分
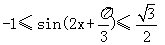 …………………………………………………10分
…………………………………………………10分
∴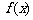 的最大值为
的最大值为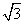 ,
, 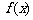 的最小值为
的最小值为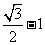 . …………………………12分
. …………………………12分
9.-4 10. 11. 25 12. 1320 13.
11. 25 12. 1320 13. 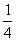 14.0,
14.0,
20. (本题满分14分)
已知数列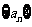 是等差数列,
是等差数列, 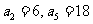 ;数列
;数列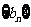 的前n项和是
的前n项和是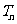 ,且
,且 .
.
(Ⅰ) 求数列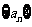 的通项公式;
的通项公式;
(Ⅱ) 求证:数列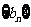 是等比数列;
是等比数列;
(Ⅲ) 记 ,求
,求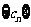 的前n项和
的前n项和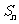 .
.
19.(本题满分14分)
曲线C上任一点到点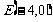 ,
,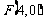 的距离的和为12, C与x轴的负半轴、正半轴依次交于A、B两点,点P在C上,且位于x轴上方,
的距离的和为12, C与x轴的负半轴、正半轴依次交于A、B两点,点P在C上,且位于x轴上方, .
.
(Ⅰ)求曲线C的方程;
(Ⅱ)求点P的坐标;
(Ⅲ)以曲线C的中心为圆心,AB为直径作圆O,过点P的直线l截圆O的弦MN长为 ,求直线l的方程.
,求直线l的方程.
18. (本题满分14分)
若函数 ,当
,当 时,函数
时,函数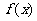 有极值为
有极值为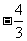 ,
,
(Ⅰ)求函数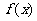 的解析式;
的解析式;
(Ⅱ)若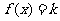 有3个解,求实数
有3个解,求实数 的取值范围。(14分)
的取值范围。(14分)
17.(本小题共12分)
某商场举行抽奖活动,从装有编为0,1,2,3四个小球的抽奖箱中同时抽出两个小球,两个小球号码相加之和等于5中一等奖,等于4中二等奖,等于3中三等奖。
(Ⅰ)求中三等奖的概率;
(Ⅱ)求中奖的概率。
16.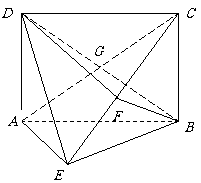 (本小题满分14分)
(本小题满分14分)
如图,矩形 中,
中, ,
, ,
,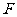 为
为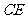 上的点,且
上的点,且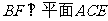 .
.
(Ⅰ)求证: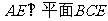 ;
;
(Ⅱ)求证; ;
;
(Ⅲ)求三棱锥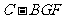 的体积.
的体积.
15. (本小题满分12分)
已知 .
.
(Ⅰ)求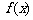 的最小正周期;
的最小正周期;
(Ⅱ)求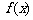 在区间
在区间 上的最大值和最小值.
上的最大值和最小值.
14.已知 是奇函数,满足
是奇函数,满足 ,当
,当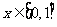 时,
时,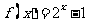 ,则
,则
 ,
,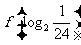 的值是
.
的值是
.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com