∵＝（a,2a,-2a）,

解法二：建立如图所示的直角坐标系,

则B（2a,0,0）,E（0,2a,0）,P（0,0,2a）,D（a,2a,0）,C（2a,a,0）,

过A作AN⊥PD于N，

∴二面角A-PD-E的大小为arcsin．                                    10分

∴在直角△AHG中，sin∠AHG＝＝．∴∠AHG＝arcsin．

在直角△PAD中，AH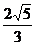＝a，

在直角△PAE中，AG＝a．

   （2）解法一：∵∠AED＝90°，

∴AE⊥ED．

∵PA⊥平面ABCDE，

∴PA⊥ED．

∴ED⊥平面PAE．

过A作AG⊥PE于G，

过DE⊥AG，

∴AG⊥平面PDE．

过G作GH⊥PD于H，连AH，

由三垂线定理得AH⊥PD．

∴∠AHG为二面角A-PD-E的平面角．                                               8分

19．（1）证明∵PA=AB=2a，PB=2a,

∴PA²+AB²=PB²，∴∠PAB=90°，即PA⊥AB．

同理PA⊥AE．                                                                                   3分

∵AB∩AE=A，∴PA⊥平面ABCDE．                                           5分

答：此人恰好两倍欠中大奖的概率是．                                  14分

P₃（2）＝C²₃（）²?（1-）^3-2=．                                     13分