
5.以下关于实验、实习的描述中,正确的一组是
①用纸层析法分离叶绿体中色素的实验结果中,黄绿色色带最宽 ②观察DNA和RNA在细胞中分布的实验中,可选用洋葱鳞片叶内表皮细胞作为实验材料,甲基绿使RNA呈绿色,毗罗红使DNA呈红色 ③鉴定还原糖时,要先加入斐林试剂甲液摇匀后,再加入乙液 ④调查蚜虫的种群密度时,可采用样方法 ⑤根尖丝分裂临时装片操作的步骤是:取材、解离、漂洗、染色、制片 ⑤用过氧化氢酶探究pH对酶活性影响的实验
中,自变量是pH,因变量是过氧化氢分解速率
A. ①②⑤⑥ B.②④⑤⑥ C.①④⑤⑥ D. ①②③④
4.雕鹗(鹰类)的下列性状分别由位于两对常染色体上的两对等位基因控制,其中有一对基因具有显性纯合致死效应(显性纯合子在胚胎期死亡)。已知绿色条纹雕鹗与黄色无纹雕鹗交配,F1为绿色无纹和黄色无纹,比例为l∶l。当F1的绿色无纹雕鹗彼此交配时,其后代(F2)表现型及比例均为绿色无纹∶黄色无纹∶绿色无纹∶黄色无纹=6∶3∶2∶1,下列有关说法错误的是
A.显性性状分别是绿色、无纹
B.F1中的绿色无纹个体都是双杂合子
C.F1中的黄色无纹个体测交后代比例为1∶1∶1∶1
D.F2中致死的个体所占的比例为l/4
3.下列有关实验过程或现象的叙述中,不正确的是
A.摘除植株的顶芽,利于降低侧芽部位的生长素浓度并促进其发育
B. 在提取叶绿体中的色素时,可用无水乙醇替代丙酮
C. 在麦芽糖酶溶液中加入班氏试剂,水浴出现砖红色沉淀
D.细胞中的线粒体可被詹纳斯绿B染液染成蓝绿色
2.手足口病是由肠道病毒等感染引起的传染病,多发生于春夏季。该病毒感染人体并侵入细胞内后,机体可以对靶细胞产生免疫反应,其中有
A. 浆细胞接触靶细胞,导致靶细胞裂解,从而使病毒被抗体消灭
B.浆细胞产生抗体,抗体接触靶细胞,导致靶细胞裂解,从而使病毒被消灭
C. 效应T细胞接触靶细胞,导致靶细胞裂解,从而使病毒被抗体消灭
D. 效应T细胞接触靶细胞,导致靶细胞裂解,从而使病毒被干扰素消灭
1.神经冲动在两个神经元之间传递时,以下生理活动不会发生的是
A.生物膜的融合和转化
B.离子通道的开放和关闭
C.ATP的合成和水解
D.信号分子与突触前膜上受体的识别和结合
7.无穷数列{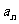 }的前n项和为Sn,
}的前n项和为Sn,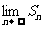 称为数列{
称为数列{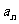 }的无穷多项和或所有项和。求
}的无穷多项和或所有项和。求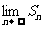 时,切不可分别求各项的极限后再求和;必须先求Sn,再求极限。若{
时,切不可分别求各项的极限后再求和;必须先求Sn,再求极限。若{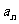 }为等比数列,公比为q且|q|<1,则
}为等比数列,公比为q且|q|<1,则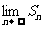 =
=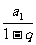 。
。
[举例1]若数列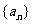 满足:
满足: 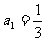 , 且对任意正整数
, 且对任意正整数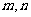 都有
都有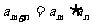 , 则
, 则
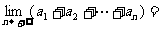 (07高考湖南理2)
(07高考湖南理2)
A.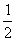 B.
B.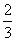 C.
C.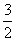 D.
D.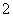
 解析:数列
解析:数列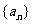 满足:
满足: 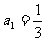 , 且对任意正整数
, 且对任意正整数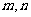 都有
都有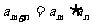 ,
,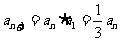 ,∴数列
,∴数列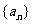 是首项为
是首项为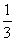 ,公比为
,公比为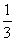 的等比数列。
的等比数列。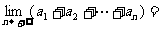
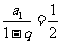 ,选A.
,选A.
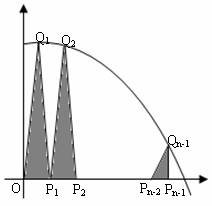
[巩固2]如图,抛物线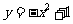 与
与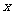 轴的正半轴交
轴的正半轴交
于点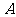 ,将线段
,将线段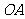 的
的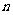 等分点从左至右依次记为
等分点从左至右依次记为
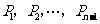 ,过这些分点分别作
,过这些分点分别作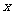 轴的垂线,
轴的垂线,
与抛物线的交点依次为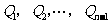 ,从而得到
,从而得到 个直角三角形
个直角三角形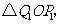
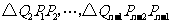 .当
.当 时,这些三角形的面积之和的极限为
.
时,这些三角形的面积之和的极限为
.
解析: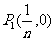 ,
,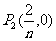 ,…,
,…,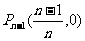 ;
;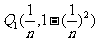 ,
,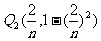 ,…,
,…,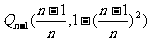 ,记
,记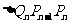 的面积为Sn,则S1=
的面积为Sn,则S1=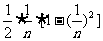 ,S2=
,S2=
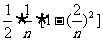 ,…,Sn-1=
,…,Sn-1=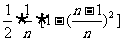 ;
; 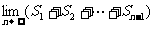 =
=
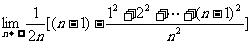 =
=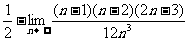 =
= =
=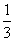 .
.
 [巩固1]数列{
[巩固1]数列{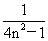 }的前n项和为Sn,则
}的前n项和为Sn,则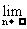 Sn=______________
Sn=______________
[巩固2] 如图,等边三角形ABC的面积等于1,连结这个三角形各边的中
点得到一个小三角形,又连结这个小三角形各边的中点得到一个更小的
三角形,如此无限继续下去,求所有这些三角形的面积的和.
[巩固3]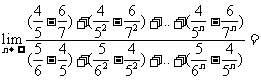 _____________
_____________
6.若|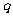 |<1,则
|<1,则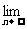
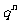 =0;
=0;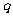 =1,则
=1,则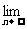
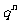 =1;若
=1;若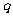 >1或
>1或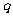 ≤-1, 则
≤-1, 则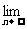
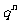 不存在。
不存在。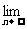
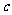
=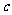 (
(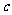 为常数);“
为常数);“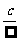 ”型的式子极限为0;“
”型的式子极限为0;“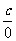 ”型、“
”型、“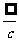 ”型的极限不存在;“
”型的极限不存在;“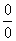 ”型和“
”型和“ ”型,一般分子、分母“同除以”一个式子(包括“约分”)后再求极限;含有根式的和(差)的式子一般有理化后再求极限。若
”型,一般分子、分母“同除以”一个式子(包括“约分”)后再求极限;含有根式的和(差)的式子一般有理化后再求极限。若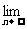
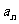 =A、
=A、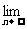
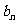 =B,则
=B,则 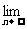 (
(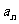 ±
±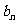 )=
A±B,
)=
A±B, 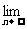 (
(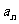
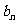 )=AB,
)=AB, 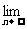
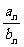 =
=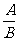 (B≠0).
(B≠0).
[举例1]若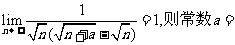 .
.
解析:分母有理化
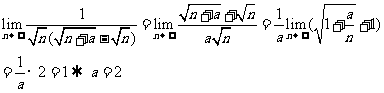
[举例2]已知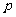 和
和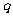 是两个不相等的正整数,且
是两个不相等的正整数,且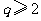 ,则
,则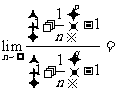 ( )
( )
A.0 B.1 C.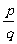 D.
D.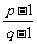 (07高考湖北理5)
(07高考湖北理5)
解析:
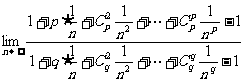
=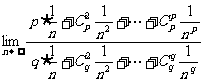 =
=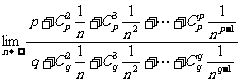 =
=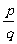 ,选C。
,选C。
[巩固1]把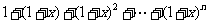 展开成关于
展开成关于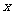 的多项式,其各项系数和为
的多项式,其各项系数和为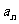 ,则
,则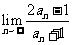 等于( )
等于( )
A. B.
B.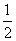 C.
C.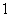 D.2
D.2
[巩固2]. n→∞lim等于( )
A. 1 B. C. D.0
[迁移]设正数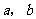 满足
满足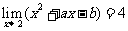 ,则
,则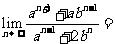 ( )
( )
A.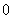 B.
B. C.
C.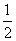 D.
D.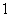 (07高考重庆理8)
(07高考重庆理8)
5.若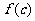 存在,则
存在,则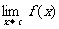 =
=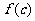 ,若
,若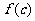 =
=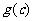 =0,则
=0,则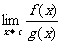 一般“约分”(约去含
一般“约分”(约去含 的因式)后再求极限。若
的因式)后再求极限。若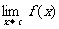 =A、
=A、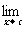
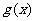 =B,则
=B,则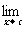 [
[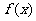 ±
±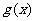 ]= A±B,
]= A±B, 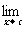 [
[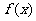
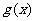 ]=AB,
]=AB, 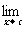
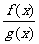 =
=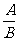 (B≠0).
(B≠0).
[举例] 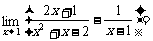 .(07高考陕西理13)
.(07高考陕西理13)
解析: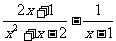 =
=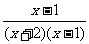 =
=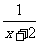 ,
,
∴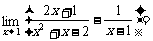
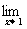
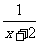 =
=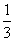
[巩固1] 下列四个命题中,不正确的是( )
A.若函数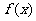 在
在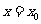 处连续,则
处连续,则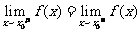
B.函数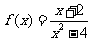 的不连续点是
的不连续点是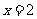 和
和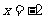
C.若函数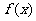 ,
,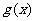 满足
满足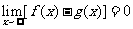 ,则
,则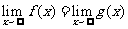
D.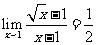 (07高考湖南理7)
(07高考湖南理7)
[巩固2]  ________
________
4.数学归纳法通常用于证明关于自然数n的等式、不等式、整除性等。用“归纳假设”即命题p(k)成立证明命题 p(k+1)成立(已知p(k)成立,求证p(k+1)成立)是数学归纳法证明中最关键的一步;而明晰命题p(k)与命题 p(k+1)之间的关系又是实现这一步的前提。
[举例1] 已知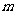 为正整数,用数学归纳法证明:当
为正整数,用数学归纳法证明:当 时,
时,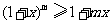 ;
;
解析:视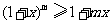 为关于
为关于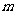 的不等式,
的不等式,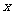 为参数,以下用数学归纳法证明:
为参数,以下用数学归纳法证明:
(ⅰ)当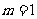 时,原不等式成立;当
时,原不等式成立;当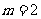 时,左边
时,左边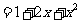 ,右边
,右边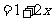 ,
,
因为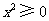 ,所以左边
,所以左边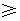 右边,原不等式成立;
右边,原不等式成立;
(ⅱ)假设当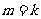 时,不等式成立,即
时,不等式成立,即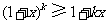 ,则当
,则当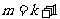 时,
时,
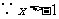 ,
, ,于是在不等式
,于是在不等式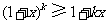 两边同乘以
两边同乘以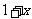 得
得
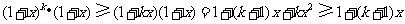 ,
,
所以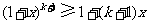 .即当
.即当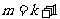 时,不等式也成立.
时,不等式也成立.
综合(ⅰ)(ⅱ)知,对一切正整数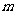 ,不等式都成立.
,不等式都成立.
[举例2]设正整数数列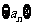 满足:
满足: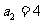 ,且对于任何
,且对于任何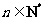 ,有
,有
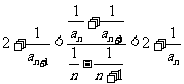 ;(1)求
;(1)求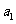 ,
,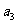 ;(2)求数列
;(2)求数列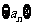 的通项
的通项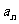 .
.
(07高考江西理22)
解析:(1)据条件得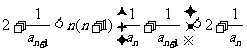 ①
①
当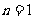 时,由
时,由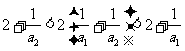 ,即有
,即有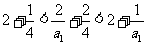 ,
,
解得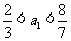 .因为
.因为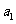 为正整数,故
为正整数,故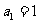 .
.
当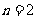 时,由
时,由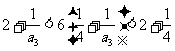 ,解得
,解得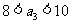 ,所以
,所以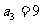 .
.
(2)由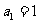 ,
,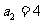 ,
,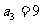 ,猜想:
,猜想: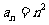 .
.
下面用数学归纳法证明.
1 当
当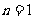 ,
,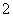 时,由(1)知
时,由(1)知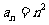 均成立;
均成立;
2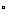 假设
假设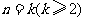 成立,则
成立,则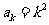 ,则
,则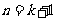 时
时
由①得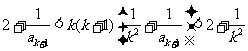
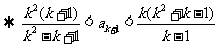
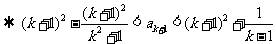
因为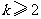 时,
时,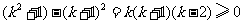 ,所以
,所以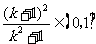 .
.
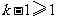 ,所以
,所以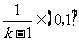 .又
.又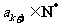 ,所以
,所以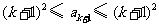 .
.
故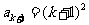 ,即
,即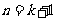 时,
时,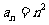 成立.由1
成立.由1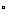 ,2
,2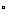 知,对任意
知,对任意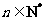 ,
,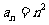 .
.
[巩固1]已知数列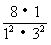 ,
,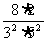 ,…,
,…,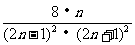 ,…;S
,…;S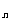 为其前n项和,求S
为其前n项和,求S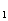 、S
、S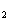 、S
、S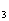 、S
、S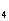 ,推测S
,推测S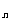 ,并用数学归纳法证明。
,并用数学归纳法证明。
[巩固2] 已知各项均为正数的数列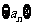 的前
的前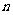 项和
项和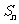 满足
满足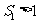 ,且
,且 ,
,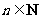 .(Ⅰ)求
.(Ⅰ)求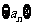 的通项公式;
的通项公式;
(Ⅱ)设数列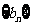 满足
满足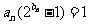 ,并记
,并记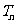 为
为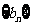 的前
的前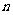 项和,求证:
项和,求证:
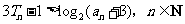 (07高考重庆理21)
(07高考重庆理21)
3.数学归纳法公理:如果关于自然数n 的一个命题p(n)满足下列条件 (1) p(n0)成立,即当n=n0时,命题成立,(2) 假设p(k)成立,则p(k+1)也成立;根据(1)(2)知命题p(n)对n≥n0的所有自然数n都成立。用数学归纳法证明问题的过程实质上是一个递推的过程,(1)是递推的基础,(2)是递推的条件;二者缺一不可。
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com