
3.1999年11月1日起,全国储蓄存款开始征收利息税,利息税的税率为20%,若将1万元人民币存入银行,年利率为2.25%,则1年后到期时,应得本金和利息共计( )
 元
元
 元
元
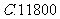 元
元
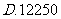 元
元
2.数列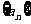 前
前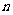 项和
项和 与通项
与通项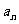 满足关系式:
满足关系式: ,则
,则 的值为
( )
的值为
( )
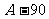
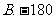


1.(2005年沈大哈长联考)已知数列{an},“对任意的nÎN*,点Pn(n,an)都在直线y=3x+2上”是“{an}为等差数列”的 ( )
A.充分而不必要条件 B.必要而不充分条件
C.充要条件 D.既不充分也不必要条件
3. 数列与平面解几何,注意用坐标与曲线的关系来打开解题思路,平时练习中还是此类问题可联系起来看
冲刺强化训练(16)
班级_____ 姓名_____ 学号_____ 日期__月__日
2.  证明:
证明: 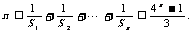 因为
因为 所以Sn是等比数列求和,但却不是等差比数列,也不是等差数列,直接求和变得不可能.观察需要证明的不等式,显然只要1££4n-1即可(数列{4n-1}的前n项和为).这类数列和式的不等式证明的关键是求和,特别是既不是等差、等比数列,也不是等差乘等比的数列求和,要利用不等式的放缩法,放缩为等比数列求和、错位相减法求和、裂项相销法求和,最终归结为有限项的数式大小比较.
所以Sn是等比数列求和,但却不是等差比数列,也不是等差数列,直接求和变得不可能.观察需要证明的不等式,显然只要1££4n-1即可(数列{4n-1}的前n项和为).这类数列和式的不等式证明的关键是求和,特别是既不是等差、等比数列,也不是等差乘等比的数列求和,要利用不等式的放缩法,放缩为等比数列求和、错位相减法求和、裂项相销法求和,最终归结为有限项的数式大小比较.
1. 在涉及指数运算的题目中,应用对数运算,十分重要,而解题过程中,一些近似运算又是十分必要的.
1. 某林场原有森林木材量为a,木材以每年的25%增长率生长,而每年冬天要砍伐的木材量为x,为了实现经过20年达到木材存有量至少翻两番的目标,则x的最大值是多少?(lg2=0.3)
2(2005南京市高三第二次质量检测)
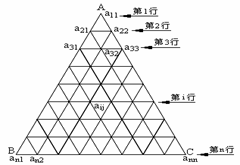
如图, 把正三角形ABC分成有限个全等的小正三角形, 且在每个小三角形的顶点上都放置一个非零实数, 使得任意两个相邻的小三角形组成的菱形的两组相对顶点上实数的乘积相等. 设点A为第一行,…, BC为第n行, 记点A上的数为 ,…, 第i行中第j个数为
,…, 第i行中第j个数为 . 若
. 若 .
.
 (1)求
(1)求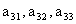 ;
;
(2)试归纳出第n行中第m个数 的表达式 (用含n , m的式子表示, 不必证明)
的表达式 (用含n , m的式子表示, 不必证明)
(3)记 证明:
证明: 
3,(2005年南京一模题)已知数列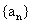 的前n项和为
的前n项和为 设集合
设集合 ,
,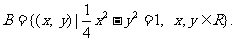
(1)
求数列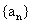 的通项公式;
的通项公式;
(2) 若以集合A中的元素作为点的坐标,则这些点是否都在同一条直线上? 并说明理由;
(3)
“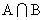 至多只有一个元素”是否正确? 如果正确, 请给予证明; 如果不正确, 请举例说明.
至多只有一个元素”是否正确? 如果正确, 请给予证明; 如果不正确, 请举例说明.
[方法点拨]
5.(2005年天津联考一)已知等差数列{an}的前n项和为Sn,且S2=10,S5=55,则过点P(n,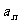 )和Q(n+2,
)和Q(n+2, )(n∈N+)的直线的一个方向向量的坐标可以是 ( )
)(n∈N+)的直线的一个方向向量的坐标可以是 ( )
A.(2,) B.(-,-2) C.(-,-1)? D.(-1,-1)
[例题探究]
4. (2005年襄樊二模题)在如图的表格中,每格填上一个数字 后,使每一横行成等差数列,每一纵行成等比数列,则a+b+c的值为
( )
A.1
B.2 C.3 D.4
(2005年襄樊二模题)在如图的表格中,每格填上一个数字 后,使每一横行成等差数列,每一纵行成等比数列,则a+b+c的值为
( )
A.1
B.2 C.3 D.4
3.已知函数 ,数列
,数列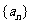 的通项公式是
的通项公式是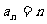 (
( ),当
),当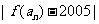 取得最小值时,
取得最小值时,
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com