
1.A 2.C 3.C 4.A 5.B
5.B
[例题探究]
例1. 分析:本题可以分析第一年末, 第二年末,…,得出第二十年末木材存量的表达式,结合“翻两番” 而列式解之.
解: 依题意得各年木材存有量如下:
第1年: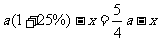
第2年: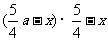
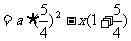
…
第20年后: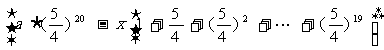
= =
=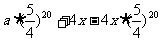
于是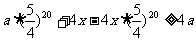 另y=
另y=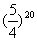 ,而lg2=0.3,
,而lg2=0.3,
则lgy=20(1-3lg2),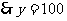
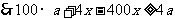 即
即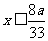
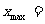
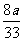 。 答:每年的砍伐量的最大值是
。 答:每年的砍伐量的最大值是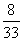 a.
a.
例2.解: (1) ∵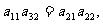 ∴
∴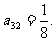 ∵
∵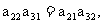 ∴
∴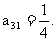
∵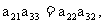 ∴
∴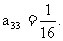 ∴
∴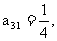
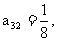
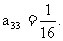
(2)由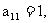
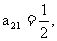
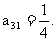 可归纳出
可归纳出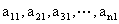 是公比为
是公比为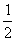 的等比数列,
的等比数列,
故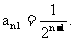 由
由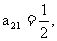
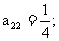
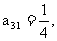
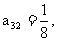
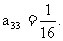
可归纳出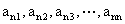 是公比为
是公比为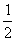 的等比数列,
的等比数列,
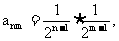
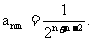
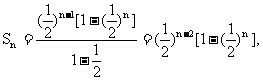
∵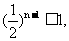 ∴
∴
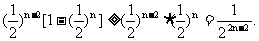
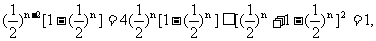
∴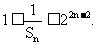 ∴
∴
例3,解析:(1)当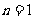 时,
时,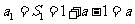
当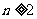 时,
时,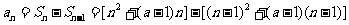 =
= .
.
可见,当n=1时,满足上式.所以,数列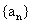 的通项公式是
的通项公式是 .
.
(2)由数列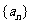 的通项公式是
的通项公式是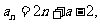 可知数列
可知数列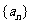 是等差数列.
是等差数列.
∴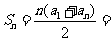
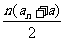 , ∴
, ∴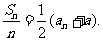
∴点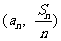 的坐标满足方程
的坐标满足方程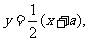
∴点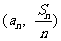 在直线
在直线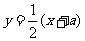 上.
上.
所以,以集合A中的元素为坐标的点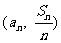 均在直线
均在直线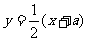 上.
上.
(3)由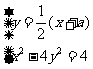 ,消去y,得
,消去y,得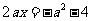
当a=0时,方程①无解,此时,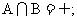
当a≠0时,方程①只有一个解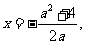
此时方程组也只有一个解,即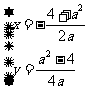
故上述方程组至多有一解,所以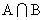 至多有一个元素.
至多有一个元素.
冲刺强化训练(16)
4.答案:A
解析:按照横行等差,纵行等比的数列特征,先计算第1、3纵行,再分别计算横行即可.a=,b=, c=,∴a+b+c=1.
1.A 2.B 3.110
9、已知函数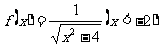 。
。
(1)求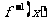 ;
;
(2)设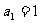 ,
,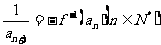 ,求
,求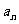 ;
;
(3)设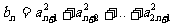 ,是否存在最小正整数m,使对任意
,是否存在最小正整数m,使对任意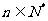 ,有
,有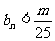 成立?若存在,求出m的值;若不存在,请说明理由。
成立?若存在,求出m的值;若不存在,请说明理由。
第16讲 数列的综合应用
[课前热身]
8.学校餐厅每天供应1000名学生用餐,每星期一有两种菜谱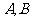 可供选择(每人选一种),调查表明:凡是在星期一选A菜谱的,下星期一会有20%改选B,而选B的,下星期一则有30%改选A,若用
可供选择(每人选一种),调查表明:凡是在星期一选A菜谱的,下星期一会有20%改选B,而选B的,下星期一则有30%改选A,若用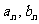 分别表示在第n个星期一选A、B的人数。
分别表示在第n个星期一选A、B的人数。
(1)试用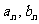 表示
表示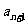 ; (2)证明:
; (2)证明: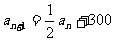 。
。
7.若干个能唯一确定一个数列的量称为该数列的“基本量”.设{an}是公比为q的无穷等比数列,下列{an}的四组量中,一定能成为该数列“基本量”的是第 组.(写出所有符合要求的组号) ①S1与S2; ②a2与S3; ③a1与an; ④q与an. 其中n为大于1的整数, Sn为{an}的前n项和.
6.定义“等和数列”:在一个数列中,如果每一项与它的后一项的和都为同一个常数,那么这个数列叫做等和数列,这个常数叫做该数列的公和.已知数列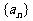 是等和数列,且
是等和数列,且 ,公和为5,那么
,公和为5,那么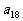 的值为______,这个数列的前n项和
的值为______,这个数列的前n项和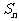 的计算公式为___ .
的计算公式为___ .
5.已知数列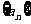 中,
中,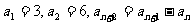 ,则
,则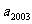 等于
( )
等于
( )
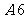
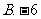
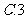
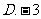
4、在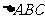 中,
中,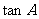 是以-4为第三项,4为第七项的等差数列的公差,
是以-4为第三项,4为第七项的等差数列的公差,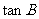 是以
是以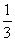 为第三项,9为第六项的等比数列的公比,则该三角形是
(
)
为第三项,9为第六项的等比数列的公比,则该三角形是
(
)
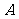 锐角三角形
锐角三角形 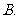 直角三角形
直角三角形
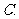 钝角三角形
钝角三角形 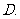 等腰三角形
等腰三角形
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com